В олимпиадах
Раздел
Темы
Сложность
13.05.2019, 19:34
Как и в любом нормальном классе, у ребят различаются предпочтения в вопросе того, где и с кем сидеть, ведь кто-то любит сидеть сзади и болтать с соседом по парте, а кому-то безразлично, где сидеть, лишь бы списать удалось. Предпочтения ребят устроены не так уж и просто: к примеру, для Миши в первую очередь важно сидеть вместе с Антоном (назовём это желанием 1 степени важности), чуть меньше его волнует то, что он любит сидеть сзади (желание 2 степени важности), и еще чуть меньше – то, что он любит сидеть у прохода (желание 3 степени важности), потому что часто выбегает попить. То есть для Миши лучше сидеть с Антоном спереди, чем с Колей или Сережей сзади, а если Мише удаётся сидеть вместе с Антоном, то лучше сзади (даже у окна), чем спереди, и т.д.
Предпочтения всех опоздавших (где и с кем сидеть) описываются следующим образом:
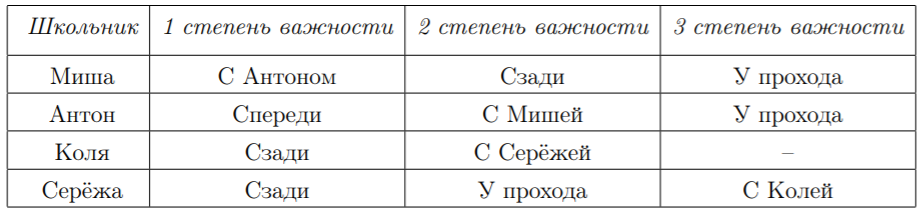
Будем называть итоговую рассадку школьников неэффективной, если опоздавшие могут перераспределить между собой эти 4 места так, чтобы хотя бы одному из них стало лучше, а остальным – не хуже. В противном случае рассадку будем называть эффективной.
(a) Приведите пример неэффективной рассадки и обоснуйте её неэффективность. Приведите пример эффективной рассадки и обоснуйте её эффективность. Сколько всего существует эффективных и неэффективных рассадок?
Взаимодействие между мальчиками происходит последовательно: первым в 9:05 приходит Миша и занимает какое-то место. Затем в 9:20 прибегают Коля и Антон, Мальчики договариваются о том, кто из них куда сядет, причем если они захотят сесть на одно и то же место, то Коле придётся уступить Антону и выбрать другое место, потому что он зачастую у него списывает и не хочет с ним спорить лишний раз. Наконец, в 9:30 прибегает Серёжа – самый сильный мальчик в классе, который без промедления занимает единственное оставшееся свободное место. Однако если Серёже не понравится это место, то он может быстро поменяться своим местом с любым из опоздавших.
(б) Все опоздавшие действуют рационально, зная о порядке взаимодействия и о предпочтениях других. Определите, может ли Миша в итоге оказаться сзади? Как в итоге рассядутся мальчики? Обязательно ли итоговая рассадка будет эффективной?
Все задачи этой олимпиады
| Задача | Баллы |
|---|---|
| Задача 1 ОЧ-2018 10 класс | |
| Задача 2 ОЧ-2018 10 класс | |
| Задача 3 ОЧ-2018 10 класс | |
| Задача 4 ОЧ-2018 10 класс | |
| Задача 5 ОЧ-2018 10 класс |
| Задача | Баллы |
|---|---|
| Задача 1 ОЧ-2018 11 класс | |
| Задача 2 ОЧ-2018 11 класс | |
| Задача 3 ОЧ-2018 11 класс | |
| Задача 4 ОЧ-2018 11 класс | |
| Задача 5 ОЧ-2018 11 класс |
| Задача | Баллы |
|---|---|
| Задача 1 ОЧ-2018 8 класс | |
| Задача 2 ОЧ-2018 8 класс | |
| Задача 3 ОЧ-2018 8 класс | |
| Задача 4 ОЧ-2018 8 класс | |
| Задача 5 ОЧ-2018 8-9 класс |
| Задача | Баллы |
|---|---|
| Задача 1 ОЧ-2018 9 класс | |
| Задача 2 ОЧ-2018 9 класс | |
| Задача 3 ОЧ-2018 9 класс | |
| Задача 4 ОЧ-2018 9 класс | |
| Задача 5 ОЧ-2018 8-9 класс |

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ