Задача
В олимпиадах
Заключительный этап ВОШ — 2009
Раздел
Баллы
12
Темы
Сложность
(5 оценок)
Автор
22.04.2009, 15:22 (Алексей Суздальцев)
03.06.2015, 13:06
03.06.2015, 13:06
Данные об экономической ситуации, с которой столкнулась некая фирма, представлены графически (даны графики выручки, предельных издержек и средней прибыли):
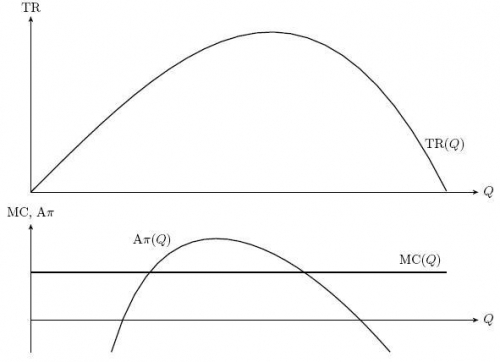
Масштаб по оси $Q$ на обоих графиках одинаковый. Определите графически оптимальный для данной фирмы объем производства и подробно опишите процесс решения.
Все задачи этой олимпиады
1-й тур: Задачи
| Задача | Баллы |
|---|---|
| Графическая-2009 | 12 |
| Задача про пиратов | 20 |
| Копыта, рога и украденная прибыль | 14 |
| Простая задача на спрос и предложение | 10 |
3-й тур: Задачи
| Задача | Баллы |
|---|---|
| В поезде «Москва-Симферополь» | 14 |
| Два касания | 20 |
| Кривая Лаффера, два зайца и тысячи рыб | 14 |
| Крококосбургер и время на готовку | 14 |
Тест
| Задача | Баллы |
|---|---|
| Возможности фермера (вопрос из теста) | 3 |

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ
Комментарии
только есть некоторые сомнения, когда он приравнивал производную нулю - там ведь не обязательно точка максимума находится, но и точка минимума тоже может быть
буквально в двух словах)
(Aп(Q)*Q)'=Aп(Q)'*Q + Aп(Q)=0 ?
А найти на графике точку с минус-единичной эластичностью можно, вспомнив, что минус-единичная эластичность должна быть и у касательной, проведенной к графику средней прибыли в этой точке... Ну а про то, где на графике линейной функции точка с минус-единичной эластичностью, много что известно...
Вообще, проведение касательной - это универсальный способ сведения неизвестной нелинейной функции к линейной, про которую много что известно.