На этой странице можно найти задачи по экономике. Прежде чем добавлять свою задачу, ознакомьтесь с руководством.

Добавить задачу на сайт

Самая свежая задача

Нетипичное производство
Обычно в задачах на производство мы считаем, что цены на факторы производства постоянны и мы можем покупать их в неограниченном количестве. Но все ресурсы в нашем мире конечны (например людской труд, скорее всего, ограничен количеством человек на планете).

Случайная задача

Макроэкономика
Найти равновесный объем национального дохода Y, если функция потребления име-
ет вид C = 40 + 0,5∙Y, а величина инвестиционных расходов равна 200 млрд. руб.
Дать алгебраическое и графическое решение данной задачи.

Авторы задач

Темы задач

Устойчивый рост

Прочитайте текст “Почему мировая экономика не демонстрировала устойчивого роста до 1800 года” и ответьте на следующие вопросы.
(Не переписывайте и не цитируйте текст в своих ответах: пишите своими словами. При этом использовать высказанные в тексте идеи не запрещается.)
В олимпиадах: 
Олимпиада ICEF Evening School — 2021
Свойства задачи: 
Качественная задача
Можно решить без знания производной

Семейный бюджет

В семье четыре человека: мама, папа, сын и дочь. Каждую неделю дети вместе с одним из родителей на весь день отправляются гулять в парк, где они обычно покупают хот-доги и мороженное. Хот-дог стоит 200 рублей, мороженое – 100 рублей. Предпочтения сына и дочери задаются функциями полезности
$u_s=\left(x_s^2-8x_s-4y_s+y_s^2\right)^{-1}$
$u_d=\left(x_d^2-4x_d-8y_d+y_d^2\right)^{-1}$
В олимпиадах: 
Олимпиада ICEF Evening School — 2021

Устойчивый рост

Прочитайте текст “Почему мировая экономика не демонстрировала устойчивого роста до 1800 года” и ответьте на следующие вопросы.
(a) “Экономическое развитие является необходимым условием для улучшения уровня жизни (богатства) людей.” Верно ли это утверждение? Почему?
(b) Объясните, как (i) примитивность финансовых отношений, (ii) неформальность контрактных институтов, (iii) зарегулированность рынков тарифами и (iv) недостаточность доходов и сбережений препятствовали экономическому росту древних экономик?
Свойства задачи: 
Качественная задача

Семейный бюджет

В семье четыре человека: мама, папа, сын и дочь. Каждую неделю дети вместе с одним из родителей на весь день отправляются гулять в парк, где они обычно покупают хот-доги и мороженное. Хот-дог стоит $200$ рублей, мороженое – $100$ рублей. Предпочтения сына и дочери задаются функциями полезности

$u_s=\left(x_s^2-8x_s-4y_s+y_s^2\right)^{-1}\ \ \ $ и $\ \ \ u_d=\left(x_d^2-4x_d-8y_d+y_d^2\right)^{-1}$

Равенство через налоги

В правительстве заметили, что для каждого гражданина страны выполняется такая закономерность: средний доход тех, кто богаче данного гражданина, превышает средний доход тех, кто его беднее, на величину $ay$, где $y$ – средний душевой доход, $a$ – некоторая положительная константа.

Будапешт на карантине

В состав Будапешта входят города Буда и Пешт, расположенные соответственно на правом и левом берегах Дуная. Местные власти каждого города регулируют жёсткость карантина таким образом, чтобы число больных коронавирусом в их городе держалось на одном уровне (он рассчитывается, исходя из количества имеющихся больничных коек). Население Будапешта равно $1$ млн $500$ тыс. человек. До эпидемии две трети из них проживали в городе Буда и одна треть – в городе Пешт, но из-за кризиса жители стали мигрировать между городами вслед за бóльшим среднедушевым доходом.
Свойства задачи: 
Можно решить без знания производной
Можно решить без знания экономической теории

Фантастические твари

По приезде в Нью-Йорк английский магозоолог Ньют Саламандер решил, что потратит весь выделенный на путешествие бюджет на себя и своих фантастических тварей. Допустим, предпочтения Ньюта можно описать функцией полезности $u(C,F)=\sqrt{C}+100\sqrt{F}$, где $C$ – деньги, которые Ньют тратит на себя, а $F$ – число универсальных наборов, которые он покупает каждой из магических тварей (коих у него $100$). Ньют выяснил, что универсальный набор по уходу за одним магическим существом в Нью-Йорке стоит ровно $5$ галлеонов.

Монопсония

На некотором рынке имеется $500$ идентичных фирм-продавцов и всего один покупатель. Функция общих издержек каждого продавца (в долларах) имеет вид $TC_i(q_i)=q_i^2$. Бюджет, который покупатель собирается потратить на данном рынке, составляет $100\ 000$ долларов.
a) Приведите реальные примеры похожих рынков.
b) Рассчитайте рыночное равновесие.

Два в одном

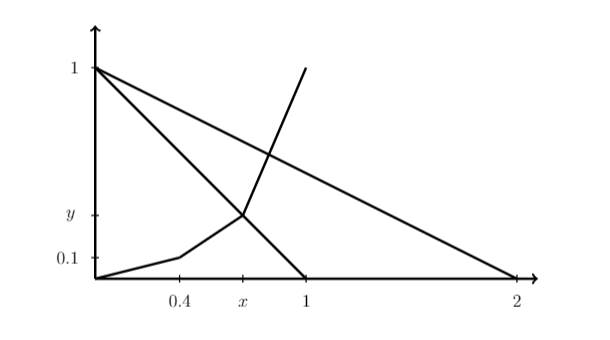Однажды Петя нарисовал кривую Лоренца для страны с тремя группами населения, доходы внутри которых равны. Он успел даже отметить точку с коодинатами $(0,4; 0,1)$, однако понял, что решает не ту задачу и аккуратно зачеркнул чертеж линиями $y=1-x$ и $y=1-0.5x$. Когда этот чертеж нашел его друг Вася, он подумал, что это кривые спроса и предельных выручки и издержек для монопльной фирмы(что вполне логично).

Спичечная логика

Однажды , два брата решили сыграть в одну очень интересную игру.Правила, которые рассказал им отец были следующие:
1.) на столе лежат три кучки спичек.
2.) в каждой кучке ровно по четыре штуки.
3.)игроки по очереди берут с любой кучки по одной или две спичке и кладут себе в карман.
4.)за один ход можно брать только с одной кучки.
5.) проигравший берёт последние спички или последнюю спичку со стола.
Свойства задачи: 
Можно решить без знания производной
Можно решить без знания экономической теории