7.4 Потоварный налог, потоварная субсидия

Потоварный налог - налог, представляющий собой фиксированную сумму, взимаемую с единицы продукции.

Рассмотрим некий рынок (возьмем для примера совершенно конкурентный). Раньше, до вмешательства государства, на данном рынке продавалось некоторое количество продукции $Q^*$ по цене $P^*$. Сумму, которую потребители уплачивали за единицу продукции, полностью получали производители. Цена покупки $P_D$ была равна цене продажи $P_S$.

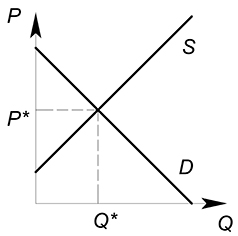
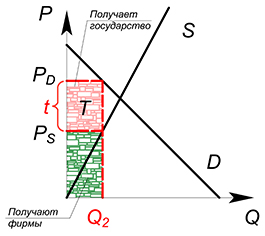
Представим, что государство ввело на данном рынке потоварный налог по ставке $t$. Теперь фирма должна, получив от покупателя сумму $P_D$ за единицу продукции, отдать государству часть этой суммы, равную ставке налога $t$. В новых условиях фирма получает сумму $P_D-t$ за единицу товара. Фактически для фирмы уменьшилась цена, по которой она продает свой продукт. $P_S=P_D-t$. При введении налога количество покупаемого и продаваемого товара уменьшается.

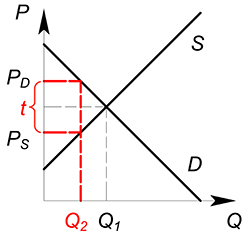
Действие, которое оказывает налог на ситуацию на рынке, эквивалентно снижению спроса или увеличению издержек. Налог, наложенный на покупателя, окажет такое же влияние на рынок, что и налог, наложенный на производителя.

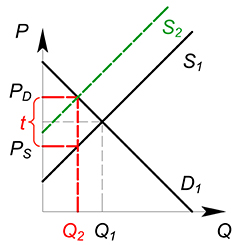
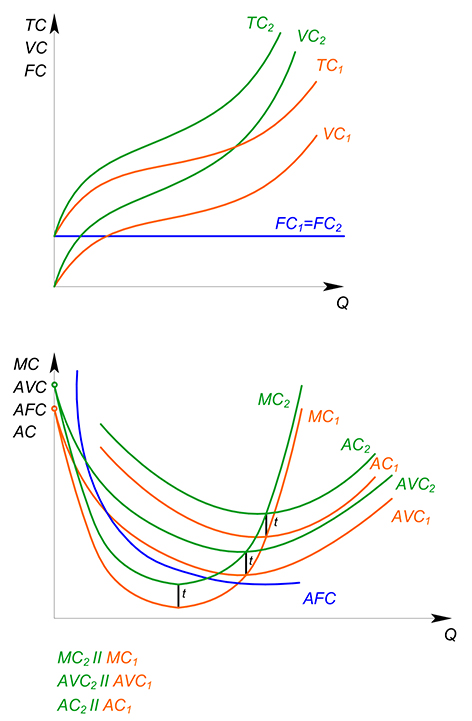
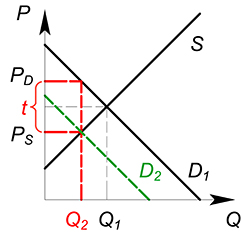Рассмотрим, какое действие оказывает налог на функции издержек одной фирмы:

$TC(Q)_2=TC(Q)_1+tQ$

Пример 1
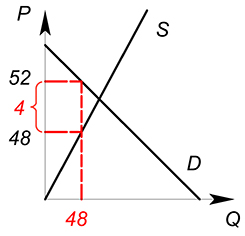
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение - $Q_S=P_S$, государство вводит налог по ставке 4, найти равновесное количество продаваемого товара, цену покупателя ($P_D$), цену продавца ($P_S$).

Решать такую задачу удобно, составив следующую систему уравнений:

$\begin {cases}
Q_D=100-P_D\\
Q_S=P_S\\
Q_D=Q_S\\
P_D=P_S+4
\end {cases}$

Отсюда получаем:

$100-(P_S+4)=P_S$

$P_S=48$

$P_D=48+4=52$

$Q_D=Q_S=48$

Пример 2
Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение - $Q_S=P_S$, государство хочет максимизировать сумму налоговых поступлений. Найдите $Q^*$, $P_D$, $P_S$, оптимальную ставку налога, сумму налоговых поступлений, построить кривую Лаффера

$\begin {cases}
Q_D=100-P_D\\
Q_S=P_S\\
Q_D=Q_S\\
P_D=P_S+t
\end {cases}$

$100-P_S-t=P_S$

$P_S=\dfrac{100-t}{2}$

$Q_S=P_S=\dfrac{100-t}{2}$

Сумма налоговых поступлений будет равна ставке налога, умноженной на количество проданного товара:

$T=t\cdot Q^*$

$T(t)=t\cdot Q(t)$

$T(t)=t\cdot (\dfrac{100-t}{2})=50t-0{,}5t^2$

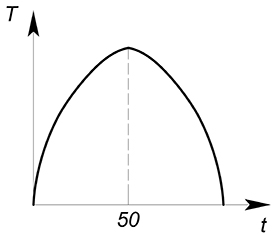
Данная функция, описывающая зависимость суммы налоговых поступлений от ставки налога, называется кривой Лаффера.

Максимизируем данную функцию:

$T'(t)=50-t$

$t^*=50$

$T''(t)=-1<0$, максимум

Теперь изобразим ее:

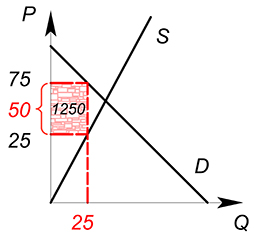
$Q_D=Q_S=25$

$P_D=75$

$P_S=25$

$T=50\cdot 25=1250$

Пример 3

Принцип введения налога на монополизированном рынке такой же как и на совершенно конкурентном.

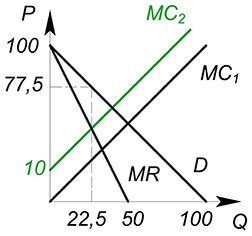
$P_D(Q)=100-Q$, $TC(Q)=Q^2+10$, $t=510$, найти прибыль фирмы после введения налога

Введем налог на продавца. Он увеличивает издержки фирмы:

$TC(Q)_2=TC(Q)_1+tQ=Q^2+10Q+10$

$\pi(Q)=100Q-Q^2-Q^2-10Q-10=90Q-2Q^2-10$

$\pi'(Q)=90-4Q=0$

$Q^*=22{,}5$

$\pi(Q)=1002{,}5>0$, фирма остается на рынке

Пример 4

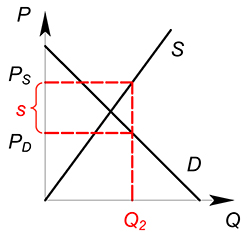
Действие потоварной субсидии обратно действию потоварного налога.

Спрос на совершенно конкурентном рынке задан функцией $Q_D=100-P_D$, предложение - $Q_S=P_S$, государство вводит субсидию по ставке 4, найти равновесное количество продаваемого товара, цену покупателя ($P_D$), цену продавца ($P_S$).

Покупатель платит за единицу товара $P_D$ меньшую $P_S=P_D+s$

$\begin {cases}
Q_D=100-P_D\\
Q_S=P_S\\
Q_D=Q_S\\
P_D=P_S-4
\end {cases}$

$100-P_S+s=P_S$

$P_S=52$

$P_D=48$

$Q_S=Q_D=52$