4.2 Фирмы на совершенно конкурентном рынке

На совершенно конкурентном рынке готовность фирм продать какое-то количество товара по какой-то цене описывается функцией предложения ($S$ - supply).

Функция предложения ($P(Q)$) показывает, какое количество товара по какой цене фирма готова продать. Рыночная функция предложения, так же как и рыночная функция спроса, получается путем суммирования индивидуальных функций предложения (функций предложения отдельных фирм).

На нерегулируемом рынке продается и покупается такое количество продукции и по такой цене, которые устраивают и продавцов, и покупателей. Равновесная цена ($P^*$) и равновесное количество ($Q^*$) продукции соответствуют точке пересечения кривых спроса и предложения.:

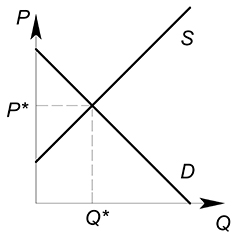
Именно цену в точке равновесия ($P^*$) каждая отдельная фирма воспринимает как заданную.
Обозначим эту цену просто за $P$. $P=const$. Тогда $TR=P \cdot Q=const \cdot Q$.
Фирма не может повлиять на цену, сложившуюся на рынке, как мы уже говорили в предыдущем уроке. Также ей невыгодно устанавливать на свою продукцию отличную от рыночной цену.

Запишем функцию прибыли некой фирмы на каком-либо совершенно конкурентном рынке:

$\pi(Q)=TR(Q) -TC(Q)=P \cdot Q-TC(Q)$

Рационально действующая фирма будет максимизировать свою прибыль. Найдем производную функции прибыли и приравняем ее к 0:

$\pi'(Q)=TR'(Q)-TC'(Q)=MR(Q)-MC(Q)=P-MC=0$

Отсюда найдем оптимальное количество производства товара, сделаем проверку на $min$/$max$. Выберем точку, где функция прибыли достигает максимального значения.

Например, это может выглядеть так:

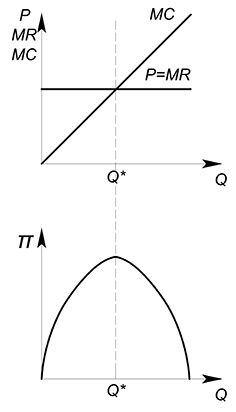
Как мы видим, обычно фирма получает максимальную прибыль в точке, где предельная выручка равна предельным издержкам. Если точка максимума функции всего одна, как в нашем примере, левее этой точки функция прибыли возрастает, такую ситуацию можно улучшить - произвести большее количество продукции и получить большую прибыль; правее этой точки функция убывает, производство каждой последующей единицы продукции будет уменьшать общую прибыль фирмы.

Для максимизации прибыли фирма выбирает для каждого возможного значения $MR$ оптимальное значение $MC$. Так как на совершенно конкурентном рынке значение предельной выручки при каждом значении $Q$ совпадает со значением цены, то функцией предложения отдельной фирмы принято считать часть ее функции предельных издержек. Для каждого значения цены фирма выберет свое оптимальное количество производимого товара, следуя правилу $MR=MC$, где в данном случае $MR=P$.

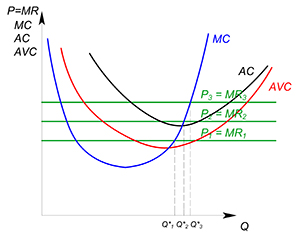
Но индивидуальной функцией предложения фирмы будет не вся ее функция предельных издержек, а только возрастающий фрагмент, лежащий выше значения функции средних переменных издержек в точке минимума.

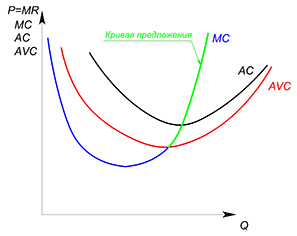
Почему именно так?

Мы выбираем возрастающий участок, ибо в точке пересечения $MR$ и $MC$ на убывающем участке функции предельных издержек функция прибыли достигает своего минимального значения - величина переменных издержек в этой точке (площадь под графиком $MC$) больше, чем величина выручки (площадь под графиком $MR$).

Фирма может работать рынке или покинуть его, если ее не будет удовлетворять получаемая прибыль. В краткосрочном периоде фирма может уйти в убыток, размер которого способен достигать значения постоянных издержек. Фирма будет оставаться на рынке до тех пор, пока получаемая выручка будет покрывать переменные издержки (пока цена продукции не будет ниже минимального значения функции средних переменных издержек; если цена опустится ниже, фирма уйдет с рынка и уже не будет предлагать продукцию):

Фирма остается, если:

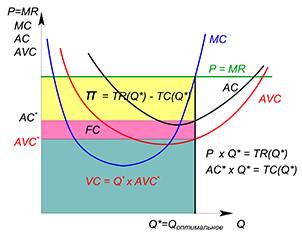
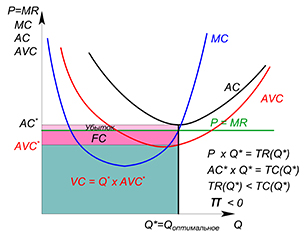
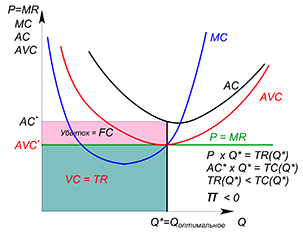
Фирма уходит, если:

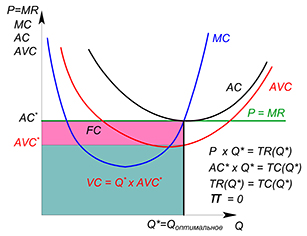
В долгосрочном периоде считается, что фирмы, получающие какие-нибудь убытки будут постепенно уходить из отрасли, рыночное предложение за счет этого будет уменьшаться, кривая рыночного предложения сдвинется влево вверх. Таким образом, равновесия цена подимется, убытки фирм, оставшихся на рынке уменьшатся. Рынок придет в равновесие. Фирмы будут получать нулевую экономическую прибыль ($\pi{экономическая}=TR-TC{экономические}$). У фирм, находящихся на рынке будут отсутствовать стимулы покидать отрасль, у фирм, потенциально способных войти на рынок, исчезнут стимулы это делать (если бы экономическая прибыль была бы положительной, этот рынок был бы сверхприбыльным, у новых фирм были бы стимулы работать на нем).

Если фирмы получают нулевую экономическую прибыль, их выручка равна экономическим издержкам, следовательно, цена равна минимуму средних общих издержек.

Пример 1
На совершенно конкурентном рынке товара установилась цена, равная 16, функция издержек фирмы имеет вид $TC(Q)=Q^2+5$, найти максимальную прибыль фирмы.

$\pi=16Q-Q^2-5$

$\pi'(Q)=16-2Q=0$

$Q^*=8$

$\pi=128-64-5=59$, $\pi>0$, фирма остется на рынке

Пример 2
На совершенно конкурентном рынке присутствуют 100 фирм, имеющих одинаковые функции издержек: $TC(Q)=Q^2+5$; спрос задан функцией $Q=100-P$, найти рыночную функцию предложения, равновесную цену и равновесное количество, если обратная функция спроса имеет вид $P=100-0{,}98Q$

Выведем индивидуальную функцию предложения каждой фирмы:

$MC(Q)=TC'(Q)=2Q$

$AVC(Q)=Q$

$AVC$ достигает своего минимального значения в точке $Q=0$, дальше $MC$ проходит всегда выше $AVC$, следовательно, в данном случае кривой предложения одной фирмы будет весь график $MC$.

Найдем рыночное предложение:

$MC=2Q$

$Q=\dfrac{MC}{2}$

$Q{рын}=\dfrac{100MC}{2}=50MC$

$MC=\dfrac{Q}{50}$

$P=\dfrac{Q}{50}$ $Q$ принадлежит $[-\infty; \infty]$

$\dfrac{Q}{50}=100-0{,}98Q$

$Q=5000-49Q$

$50Q=5000$

$Q^*=100$

$P^*=\dfrac{100}{50}=100-0{,}98 \cdot 100 =2$