В олимпиадах
Баллы
Темы
Свойства
Сложность
Автор
17.04.2024, 19:44
(0)
После того, как администратор расселил ребят по комнатам, ребятам можно меняться соседями. Для этого двое детей должны подойти к администратору и сказать, что они хотят жить друг с другом больше, чем со своими текущими соседями. Назовём стабильным такое расселение ребят, при котором никакая пара ребят не хочет подойти к администратору для совершения обмена.
Примечание. Задача является примером применения дизайна механизмов, о котором можно узнать больше из материалов просветительского проекта РЭШ GURU.
а) Пусть администратору надо расселить ровно 4 ребёнка. Сколько всего расселений возможны?
б) Может ли в этом случае быть ровно одно стабильное расселение? А два? А три? Если вы считаете, что может, приведите пример. Если нет, докажите невозможность.
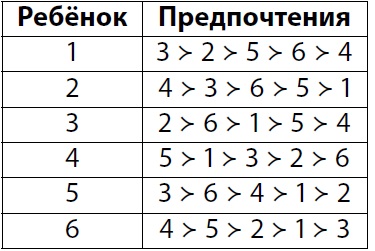
в) Предположим, что администратору нужно расселить 6 детей. Для удобства занумеруем их от 1 до 6. Их предпочтения представлены в таблице ниже. Выражение $i \succ j$ означает, что, по мнению ребёнка, сосед $i$ лучше соседа $j$. Найдите все стабильные расселения и докажите, что других не существует.
Все задачи этой олимпиады
| Задача | Баллы |
|---|---|
| Кто не рискует | 27 |
| Мысли стратегически! | |
| О наградах | 15 |
| О стоимости жизни | 18 |
| Оптимальное расселение | 25 |
| Поработаем вместе? | 13 |
| Эффекты полицейского насилия | 16 |

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ