Задача
В олимпиадах
Региональный этап ВОШ — 2009
Баллы
8
Темы
Сложность
(3 оценок)
Автор
08.02.2009, 12:15 (Алексей Суздальцев)
03.06.2015, 12:53
03.06.2015, 12:53
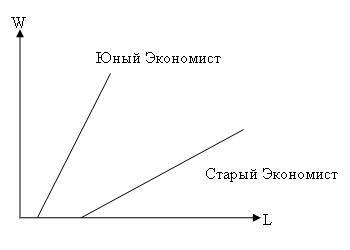
Поспорил как-то Юный Экономист со Старым Экономистом о том, чья кривая предложения труда эластичнее при одном и том же уровне заработной платы.
- Конечно, моя, - раздраженно доказывал Старый Экономист,- ты посмотри, какой у нее наклон! Да и при нулевой зарплате я готов на большее! А если мне ее еще и поднимут...
- А ты разве забыл, что эластичность и наклон - совсем не одно и то же?! Эластичнее моя кривая предложения, так как она ближе к началу координат. А там, говорят, эластичность чуть ли не единичная! - гордо отвечал Юный Экономист.
Спорили они так до вечера, пока не пришел Умный Экономист и не разрешил их спор. Попробуйте и вы сделать то же самое: выясните, чья кривая предложения труда эластичнее при каждом конкретном уровне заработной платы. Решение должно быть выполнено на основе приведенного ниже графика, на котором изображены кривые предложения труда обоих экономистов.
Все задачи этой олимпиады
| Задача | Баллы |
|---|---|
| Неравенство среднедушевых доходов | 12 |
| Новогоднее предложение от монополиста | 16 |
| Четырехмерный коктейль | 10 |
| Эластичностный конфликт поколений | 8 |
Факультет экономических наук НИУ ВШЭ
Комментарии
Обе кривые выходят из одной точки, что означает что кривая 2 отличается от кривой 1
увеличением предложения в n раз.
То есть если первая кривая имеет вид Ls = 10+2w то вторая Ls = 20+4w
А посему при одинаковой w эластичности в этих точках одинаковы.
Или: провести кривую W а затем определить эластичность в точках по отрезкам
Просто немного по-другому сказано. "Метод отрезков", по сути, в этом решении и доказывается.