Выручка (TR) - это доход (денежная сумма), который фирма получает от продажи по некоторой цене какого-то количества произведенной продукции:
$TR=P\cdot Q$
Функция выручки - зависимость между количеством производимого блага и величиной денежной суммы, получаемой от продажи товара. Функция выручки выводится из спроса:
$TR=P(Q)\cdot Q$
Функции выручки могут иметь совершенно разнообразный вид:
Пример 1
Функция спроса описывается зависимостью $Q(P)=\dfrac{100}{P}$. Найти функцию выручки.
Выразим обратную функцию спроса: $P(Q)=\dfrac{100}{Q}$; теперь найдем функцию выручки: $TR=\dfrac{100}{Q} \cdot Q=100$. В данном случае выручка постоянна, не зависит от количества производимого блага и равна 100.
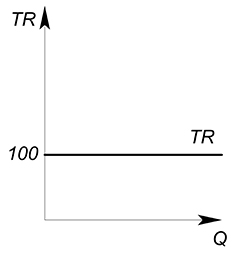
Подробнее о функции выручки мы будем говорить, когда будем изучать рыночные структуры.
Определение 2
Средняя выручка (AR - average revenue) показывает, какую выручку в среднем приносит единица продаваемого товара:
$AR=\dfrac{TR}{Q}$
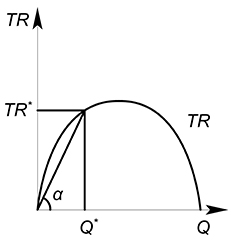
Геометрический смысл средней выручки - тангенс угла наклона луча (секущей), проведенного из начала координат к какой-нибудь точке на графике выручки:
$tg \alpha = \dfrac {TR^*}{Q^*}$
Проведя огромное количество лучей к графику выручки мы сможем получить график средней выручки $AR$.
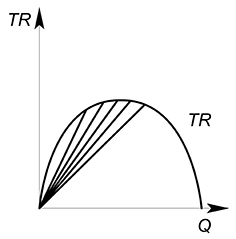
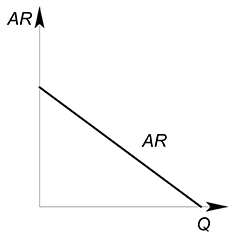
Так среднюю выручку можно описать функцией, вид которой будет совпадать с обратной функцией спроса:
$AR=\dfrac{TR(Q)}{Q}=P(Q)$
 Определение 3
Определение 3
Предельная выручка (MR - marginal revenue) показывает, какую выручку принесет дополнительная произведенная единица товара.
В дискретном случае предельная выручка будет равна $MR=\dfrac {TR_2-TR_1}{Q_2-Q_1}=\dfrac{\Delta TR}{\Delta Q}$
Геометрический смысл предельной выручки - тангенс угла наклона секущей, соединяющей точки $(Q_2;TR_2)$ и $(Q_1;TR_1)$.
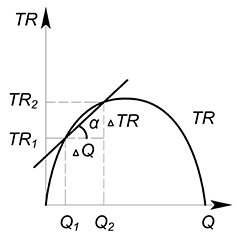
Если мы предполагаем, что производимый нами товар является бесконечно делимым, то нам будет интересно узнать какую выручку принесет дополнительная бесконечно малая единица выпускаемого блага.
Тогда геометрический смысл в данном случае будет следующий: MR есть тангенс угла наклона касательной, проведенной к графику функции выручки в интересующей нас точке.
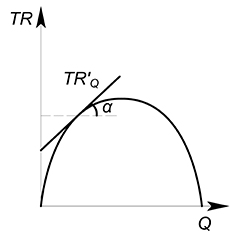
Проведя множество касательных к разным точкам сможем построить функцию предельной выручки:
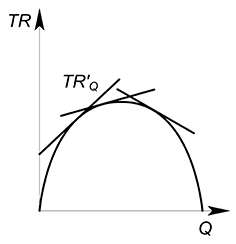
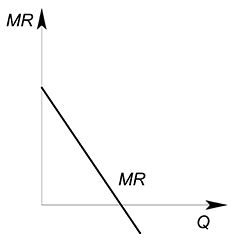
В данном случае предельная выручка будет производной функции выручки: $MR(Q)=TR'(Q)$.
Пример 2
Функция спроса описывается уравнением $Q(P)=10-P$. Найти функции TR, AR, MR и изобразить их графики.
Выразим обратную функцию спроса: $P(Q)=10-Q$. Теперь найдем функцию выручки: $TR(Q)=P(Q)\cdot Q=10Q-Q^2$. Можно найти функции средней и предельной выручки: $AR(Q)=\dfrac {TR(Q)}{Q}=10-Q$, $MR(Q)=TR'(Q)=10-2Q$. Изобразим графики:
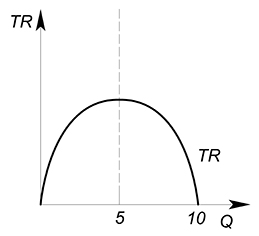
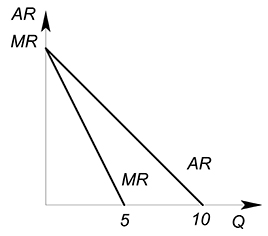 Максимизация функции выручки выполняется так же, как и любой другой функции - можно использовать производную (подробнее о максимизации функции можете узнать здесь), а можно обойтись без нее (подробнее здесь)
Максимизация функции выручки выполняется так же, как и любой другой функции - можно использовать производную (подробнее о максимизации функции можете узнать здесь), а можно обойтись без нее (подробнее здесь)
Пример 3
Обратная функция спроса имеет вид: $P(Q)=20-2Q$. Найти максимальную выручку.
Запишем функцию выручки: $TR=20Q-2Q^2$. Это парабола, ветви вниз. Найдем точку максимума: $x_0=-\dfrac{b}{2a}=\dfrac{20}{4}=5$. Подставим данную точку в функцию выручки: $TR=20\cdot 5-2\cdot 25=100-50=50$.
Также для функции $AR$ $TR$ в точке будет является произведением значений координат на осях:
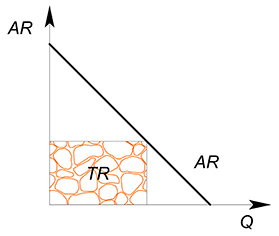
для $MR$ - $TR$ в точке есть площадь под графиком функции, слева ограниченная осью $P$, справа перпендикуляром к оси $Q$, проведенным из интересующей нас точки:
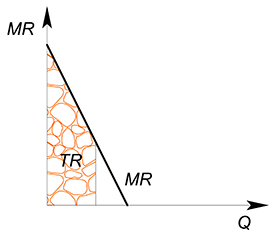



 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ