Обычно в задачах на производство мы считаем, что цены на факторы производства постоянны и мы можем покупать их в неограниченном количестве. Но все ресурсы в нашем мире конечны (например людской труд, скорее всего, ограничен количеством человек на планете).

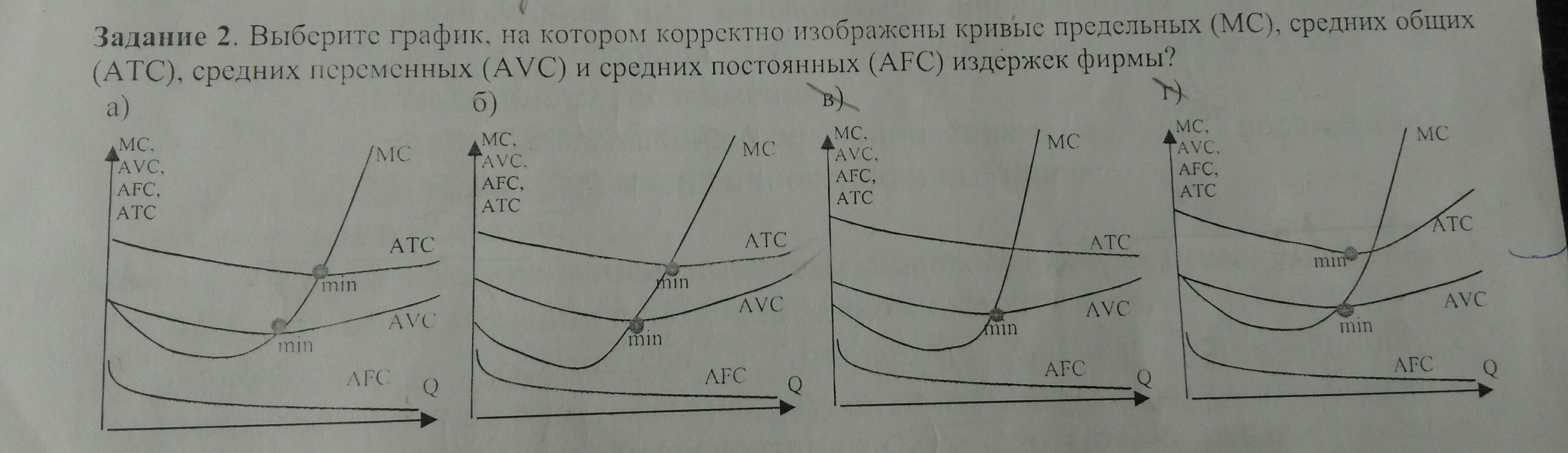 Выберете график, на котором корректно изображены кривые предельных (MC), средних общих (ATC), средних переменных (AVC) и средних постоянных (AFC) издержек фирмы?
Выберете график, на котором корректно изображены кривые предельных (MC), средних общих (ATC), средних переменных (AVC) и средних постоянных (AFC) издержек фирмы?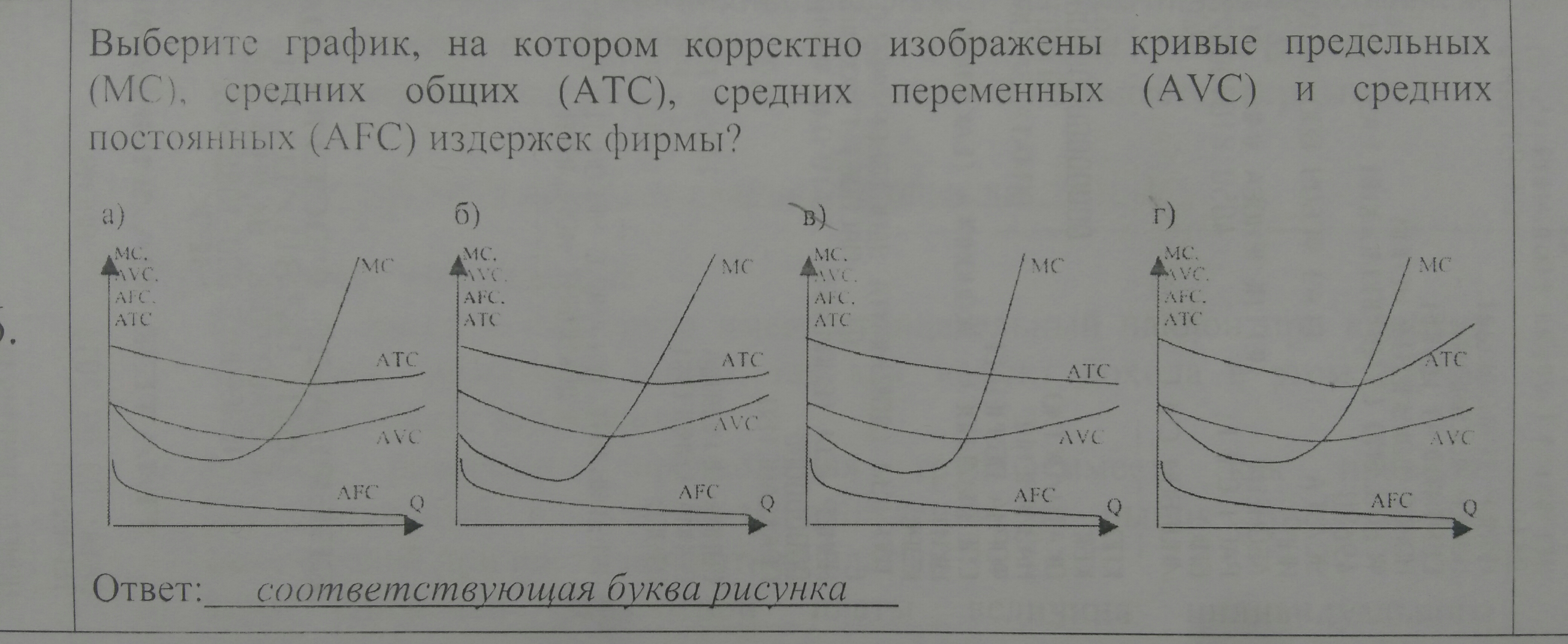
 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ