Задача
В олимпиадах
Заключительный этап ВОШ — 2021
Раздел
Баллы
12
Темы
Свойства
Сложность
Голосов еще нет
20.02.2022, 16:53 (Дарья Елицур)
20.02.2022, 20:09
20.02.2022, 20:09
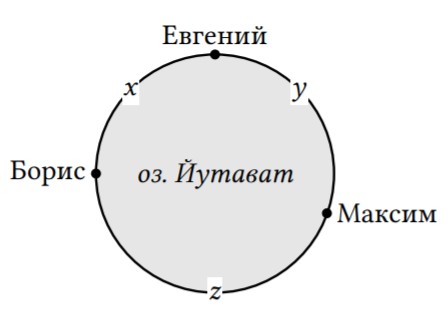
Озеро Йутават представляет собой идеальный круг. Борис, Евгений и Максим ловят в этом озере рыбу и продают ее местным жителям, которые живут вокруг озера. Каждый день рыбаки независимо друг от друга выбирают, в каких точках на берегу (окружности) озера организовать продажу рыбы. Жители распределены вокруг озера равномерно (то есть на каждый километр расстояния вдоль окружности приходится одинаковое и достаточно большое число жителей). Цена килограмма рыбы исторически сложилась на определенном уровне, она достаточно высока, чтобы окупать усилия и снасти рыбаков, никто из них не считает уместным ее менять. Каждый рыбак ловит достаточно много рыбы, чтобы хватило любому количеству потребителей.
Каждый местный житель потребляет по 1 килограмму рыбы в день, покупая ее у ближайшего из трех рыбаков (по расстоянию, которое нужно проделать по окружности). Если расстояние от потребителя до двух ближайших рыбаков одинаково, то он принимает решение произвольным образом (этим потребителем можно пренебречь). Рыбаки, таким образом, конкурируют за потребителей, и каждый из них хочет выбрать своё расположение на берегу озера так, чтобы максимизировать выручку. Два или три рыбака могут выбрать одну и ту же точку для продажи, в таком случае они будут делить выручку на равные части.
По итогам каждого дня каждый рыбак оценивает объем продаж за день и следующим образом принимает решение, где организовать продажи на следующий день:
Каждый местный житель потребляет по 1 килограмму рыбы в день, покупая ее у ближайшего из трех рыбаков (по расстоянию, которое нужно проделать по окружности). Если расстояние от потребителя до двух ближайших рыбаков одинаково, то он принимает решение произвольным образом (этим потребителем можно пренебречь). Рыбаки, таким образом, конкурируют за потребителей, и каждый из них хочет выбрать своё расположение на берегу озера так, чтобы максимизировать выручку. Два или три рыбака могут выбрать одну и ту же точку для продажи, в таком случае они будут делить выручку на равные части.

По итогам каждого дня каждый рыбак оценивает объем продаж за день и следующим образом принимает решение, где организовать продажи на следующий день:
- Если его сегодняшнее положение принесло ему максимальную дневную выручку среди всех вариантов его размещения (с учетом фактического положения двух других), то на следующий день он остается в той же точке.
- Если условие предыдущего пункта не выполнено, он выбирает какую-то другую точку, в которой при текущем расположении других рыбаков его выручка была бы больше.
По прошествии нескольких дней все рыбаки решили больше никуда не двигаться и навсегда остались в некоторых точках (такое расположение является равновесием Нэша в этой задаче). Опишите их все возможные финальные расположения через ограничения на параметры $x, y, z$ (расстояния между рыбаками). Считайте, что длина окружности $x+y+z=1$
Все задачи этой олимпиады
Второй тур: 10 класс
| Задача | Баллы |
|---|---|
| Рынок заёмных средств | 12 |
Второй тур: 11 класс
| Задача | Баллы |
|---|---|
| Макроэкономика коронакризиса | 12 |
Второй тур: 9 класс
| Задача | Баллы |
|---|---|
| Рынок заёмных средств | 12 |
Первый тур: 10 класс
| Задача | Баллы |
|---|---|
| "Вычитание" КПВ | 12 |
| Блиц | 12 |
| Круглое озеро | 12 |
| Эксперимент с медицинским страхованием | 12 |
Первый тур: 11 класс
| Задача | Баллы |
|---|---|
| "Вычитание" КПВ | 12 |
| Блиц | 12 |
| Максимизируем выручку, чтобы максимизировать прибыль | 12 |
| Эксперимент с медицинским страхованием | 12 |
Первый тур: 9 класс
| Задача | Баллы |
|---|---|
| "Вычитание" КПВ | 12 |
| Блиц | 12 |
| Голосование о торговле | 12 |
| Круглое озеро | 12 |

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ