2.3 Сложение некоторых КПВ

1. Рассчитываем суммарные крайние точки (или одну крайнюю точку)
2. Рассматриваем $AC$ какого-нибудь товара на всех участках всех КПВ
3. Располагаем эти участки в соответствии с законом возрастающей $AC$

Пример 1
Найдите суммарную КПВ двух стран:

Данные КПВ являются линейными функциями.

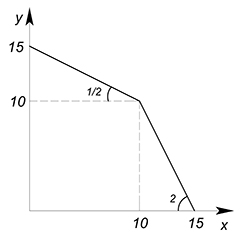
Рассчитаем суммарные крайние точки данных КПВ: по $y$: $10+5=15$, по $x$: $5+10=15$.

Рассмотрим $AC_x$: первая функция обладает постоянной (ибо функция линейная) $AC_x=\dfrac{10}{5}=2$; вторая функция обладает также постоянной $AC_x$, но уже равной $\dfrac{5}{10}=\dfrac{1}{2}$. Первый участок суммарной КПВ будет представлен функцией с меньшей $AC_x=\dfrac{1}{2}$, а на втором участке $AC_x=2$.

Пример 2
Найдите суммарную КПВ двух стран:

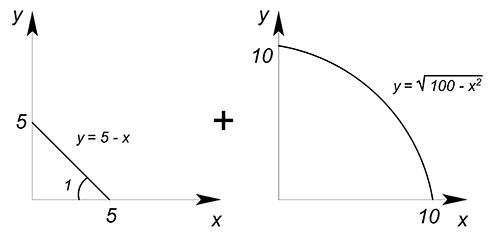
В данном случае мы имеем одну линейную и одну вогнутую КПВ.

Крайние точки суммарной КПВ: по $y$: $5+10=15$, по $x$: $5+10=15$.

Теперь перейдем к оценке альтернативной стоимости. У линейной функции она постоянна и по $x$ равна $\dfrac{5}{5}=1$. $AC_x$ вогнутой функции не является константой. Она возрастает на при движении вдоль оси $x$ ($tg$ углов наклона касательных, проведенных к каждой точке данного графика возрастают). Для построения суммарной КПВ необходимо расположить участки в соответствии с законом возрастающей альтернативной стоимости. Поэтому нам надо найти на вогнутой КПВ участки, где $AC_x>1$ и где $AC_x<1$. Найдем точку, в которой $AC_x=1$. $tg$ угла наклона касательной, взятый по модулю, в ней должен равняться $1$, производная данной функции в этой точке тоже должна быть равна $1$:

$y(x)= \sqrt{100-x^2}$
$y'(x)=|\dfrac{-x}{\sqrt{100-x^2}}|=|-1|$
$x^2=100-x^2$
$x^2=50$
$x=5\sqrt{2}$

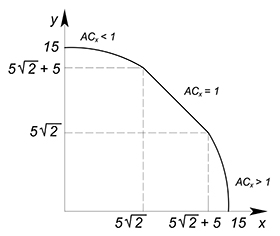
Очевидно, что $AC_x$ на участке, располагающемся слева от этой точки меньше $1$, а на находящемся справа больше.

Размещаем наши фрагменты двух КПВ по правилу, получаем: первый кусочек с $AC_x<1$ является частью вогнутой функции, второй есть линейная функция с $AC_x=1$, третий - оставшийся фрагмент вогнутой функции с $AC_x>1$.

При совместном производстве благ тот или иной товар будет производить тот субъект, у которого это получается лучше всего (то есть с наименьшими альтернативными издержками). В такой ситуации ресурсы каждого производителя будут использоваться максимально эффективно, ибо они будут задействованы в создании того блага, для которого подходят лучше всего (например, если мы выращиваем морковь и ловим рыбу, то в данном случае лопатой будут копать, а не использовать её вместо весла). Поэтому, работая вместе, две страны смогут произвести больше благ, чем при индивидуальной работе.