2.2 Построение КПВ

При решении задач мы используем все имеющиеся ресурсы, если объём производства каждого товара возрастает по количеству используемого фактора производства (иначе использовать не все будет неэффективно).

Товары, производство которых описывает КПВ, имеют определенные технологии изготовления. На основании информации об этих технологиях можно построить и сам график функции КПВ. Рассмотрим следующие примеры:

На изготовление единицы товара $x$ уходит $5$ часов, для производства единицы товара $y$ требуется $2$ рабочего времени, всего имеется 20 рабочих, готовых трудиться по $160$ часов в месяц. Найдите функцию КПВ и постройте её график.

"На изготовление единицы товара $x$ уходит $5$ часов..." Единица $x$ стоит 5 часов труда, следовательно, количество единиц товара $x$ в $5$ раз меньше количества затраченных на неё часов труда: $L_x=5x$ ($L$-$labour$-труд). Аналогично для товара $y$: $L_y=2y$. Всего в экономике имеется $L_{общ}=160\cdot{20}=3200$ часов труда. Получаем:

$L_x+L_y=L_{общ}$

$5x+2y=3200$

В привычной форме:

$y=1600-2{,}5x$

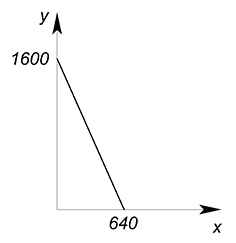Технология производства товара $x$ задаётся функцией $x=\sqrt{L_x}$, для производства единицы товара $y$ также требуется $2$ рабочего времени, и опять имеется 20 рабочих, готовых трудиться по $160$ часов в месяц. Найдите функцию КПВ и постройте её график.

$x=\sqrt{L_x}$

Выразим $L_x$:

$L_x=x^2$

$L_y=2y$.

Всего в экономике имеется $L_{общ}=160\cdot{20}=3200$ часов труда.

Получаем:

$L_x+L_y=L_{общ}$

$x^2+2y=3200$

$y=1600-0{,}5x^2$

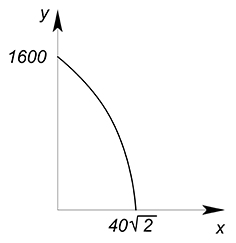В общем виде:

$L_x=...$

$L_y=...$

$L_x+L_y=L_{общ}$

$y=f(x)$

P.S. В случае, когда нам для представления КПВ в привычном виде ($y=f(x))$ необходимо извлечь корень из какого-то выражения, естественно, мы получаем $2$ ответа: с плюсом и с минусом. Нам необходимо взять тот, что с плюсом, ибо $y$ не может быть отрицательным Пример:

$x^2+y^2=100$

$y2=100-x^2$

$y=-\sqrt{100-x^2}$ данный корень нам не подходит

$y=\sqrt{100-x^2}$ данный корень нам подходит