2.4 Оптимизация на КПВ

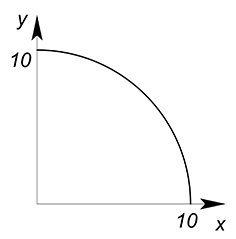
Имеем: КПВ некоторый страны задана функцией $x^2+y^2=100$, цены товаров $x$ и $y$ соответственно равны $10$ и $5$, найти при каком объёме производства данных товаров выручка от их продажи будет максимальной.

Построим КПВ:

$x^2+y^2=100$

$y^2=100-x^2$

$y=\sqrt{100-x^2}$

Теперь разберемся с функцией выручки (выручка обозначается буквами $"TR"$ (от англ "total revenue")):

$TR=PQ$, где $P$ - цена товара, $Q$ - его количество.

В данном случае у нас $2$ товара, поэтому функция $TR$ будет зависеть от двух переменных $Q_x$ и $Q_y$:

$TR=P_xQ_x+P_yQ_y=10Q_x+5Q_y$

Далее для простоты будем писать не $Q_x$, $Q_y$, а просто $x$, $y$

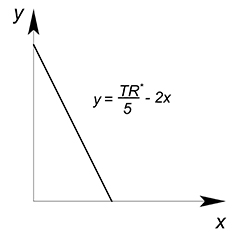
Данная функция выручки может быть построена в трехмерной плоскости. Что мы можем сделать с этой функцией, чтобы перевести её в двухмерное пространство? В первую очередь можно выразить $y$ через $2$ другие переменные ($TR$;$x$):

$y=\dfrac{TR}{5}-2x$.

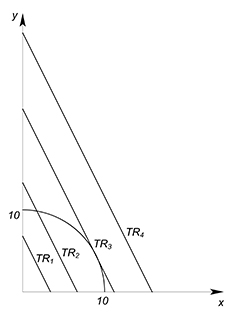
Так как значение $TR$ нам не задано, мы можем сами выбрать оптимальную для нас величину выручки. Будем фиксировать значение $TR$ на разных уровнях (будем преходить на более высокие графики - увеличивать значение выручки), пока не достигнем оптимального ($TR_1 \to TR_2 \to TR_3$). $TR_3$ будет оптимальной величиной, ибо точка, в которой функция выручки касается графика КПВ, будет на границе нашей области производственных возможностей, следовательно, точка касания будет приносить максимальную выручку, а график выручки будет занимать самое высокое положение из всех доступных (выручка будет наибольшей из всех возможных). Если бы мы выбрали меньшее значение выручки, то мы недополучили бы часть денег - мы смогли бы произвести ещё больше товаров $x$ и $y$ и продать их (в этом случае у нас была бы возможность улучшения ситуации). Если бы выбрали большее значение переменной $TR$ ($TR_4$), то не смогли бы произвести соответствующий ей объём товаров, ибо нет такой точки (с точки зрения производства), в которой мы бы получили такую выручку.

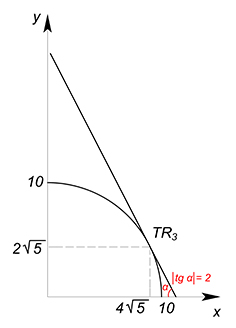
Как мы уже выяснили, оптимальная точка будет лежать на графике КПВ. Её положение на данной линии будет зависеть от соотношения цен товаров $x$ $y$, которые и задают наклон функции выручки.

Линейная функция $y=\dfrac{TR}{5}-2x$ будет иметь постоянный $tg$ угла наклона, равный по модулю $2$. Чтобы найти положение оптимальной точки на графике КПВ необходимо взять производную функции КВП (обычно это делается по переменной $x$) и приравнять её к производной функции выручки (взятой также по $x$ - $y'(x)$) . То есть угол наклона касательной в оптимальной точке должен совпадать с углом наклона функции выручки.

КПВ:
$y=\sqrt{100-x^2}$
$y'(x)=\dfrac{-x}{\sqrt{100-x^2}}$

$TR$:
$y=\dfrac{TR_3}{5}-2x$
$y'(x)=-2$

$\dfrac{-x}{\sqrt{100-x^2}}=-2$

Отсюда находим $x$ и соответствующее ему значение $y$:

$x=4\sqrt5$
$y=2\sqrt5$

Считаем выручку:

$TR=10\cdot{4\sqrt5}+5\cdot{2\sqrt5}=50\sqrt5$

У этой задачи есть более легкое и быстрое решение: подставляем функцию КПВ вместо переменной $x$ в функции выручки:
$TR=10x+5\sqrt{100-x^2}$
Получаем функцию, зависимую от одной переменной. Максимизируем данную функцию обычным способом, беря производную и приравнивая её к 0.

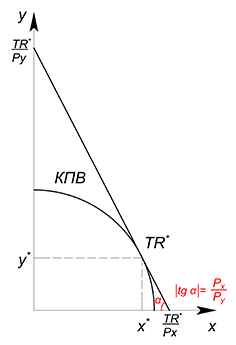
В общем виде:

КПВ:
$y=f(x)$

$TR$:
$TR=P_x\cdot{x}+P_y\cdot{y}$
$y=\dfrac{TR}{P_y}-\dfrac{P_xx}{P_y}$

Фиксируем $TR$=$TR^*$ на некотором оптимальном уровне:

$y=\dfrac{TR^*}{P_y}-\dfrac{P_x\cdot{x}}{P_y}$

Берем производные функций КПВ и выручки, приравниваем их:

$f'(x)=-\dfrac{P_x}{P_y}$

Находим оптимальные $x$, $y$, $TR$

Особого внимания заслуживает случай с линейной функцией КПВ (аналогично поступаем и с выпуклой).
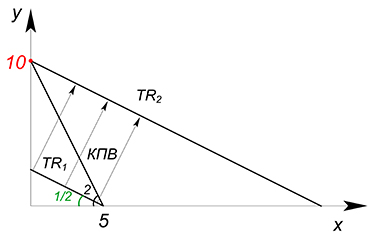
Имеем: КПВ задана функцией $y=10-2x$; $P_x=5$, $P_y=10$. Найти максимальную выручку.
В данном случае у нас нет возможности провести касательную к графику функции КПВ, но мы также можем воспользоваться методом фиксации значения $TR$ и поиска оптимальной точки.

$TR=5x+10y$
$y=\dfrac{TR^*}{10}-\dfrac{x}{2}$

Точно также будем двигать в право функцию выручки, пока она не займет наивысшее положение из всех возможных - пока значение выручки, приносимой комбинациями $x$ и $y$, не станет максимальным из всех доступных. Максимальную выручку в данном случае мы можем получить в точке $y=10$, $x=0$. Считаем $TR=10\cdot{10}=100$. При линейной функции КПВ метод тот же, но функция выручки уже не будет касательной.

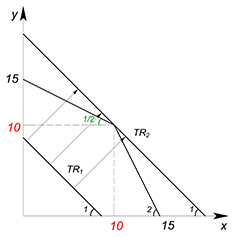
Также интересен случай с функцией КПВ, имеющей излом. Воспользуемся тем же методом, что и в двух предыдущих случаях, только опять же здесь функция выручки не будет касательной, проведенной к графику КПВ.

Имеем: график КПВ состоит из двух участков, заданных функциями $y=15-\dfrac{x}{2}$ при $x$ принадлежащем $[0;10]$, $y=30-2x$ при $x$ принадлежащем $[10;15]$. $P_x=P_y=5$.

$TR=5x+5y$
$y=\dfrac{TR}{5}-x$

Двигаем график выручки вправо, пока он не займет максимально доступное значение. В данном случае это значение оказалось в точке излома графика КПВ (такое бывает не всегда). Так случилось, потому что угол наклона графика выручки был меньше угла наклона одной из функций КПВ, но больше угла наклона второй.

$x=y=10$
$TR=5\cdot{10}+5\cdot{10}=100$

В общем виде:

КПВ:
$y=f(x)$

$TR$:
$TR=P_x\cdot{x}+P_y\cdot{y}$
$y=\dfrac{TR}{P_y}-\dfrac{P_xx}{P_y}$

Фиксируем $TR$=$TR^*$ на некотором оптимальном уровне:

$y=\dfrac{TR^*}{P_y}-\dfrac{P_x\cdot{x}}{P_y}$

Двигаем функцию выручки вправо, пока не достигнем наибольшего уровня $TR$ из всех возможных. Находим соответствующие точке пересечения значения $x$, $y$, $TR$.

Вообще весь данный метод поиска максимальной выручки основан на фиксации переменной $TR$ и её движении вправо до того момента, пока мы не достигнем максимально высокого уровня графика, которому соответствует максимально возможное значение выручки и оптимальные $x$ и $y$. Просто методы подсчета этих оптимальных значений товаров различны для различных функций КПВ.

Еще одним распространённым типом задач является поиск оптимальных объёмов производства товаров при заданной пропорции их потребления.

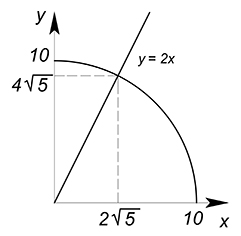
КПВ некоторой страны задана функцией $x^2+y^2=100$. Жители потребляют товары $x$ и $y$ только в пропорции $\dfrac{1}{2}$. Найти оптимальные объёмы производства данных благ.

Как обычно начнем с построения КПВ

Далее у нас имеется ограничение - потребление $x$ и $y$ в определенной пропорции. Если $\dfrac{x}{y}=\dfrac{1}{2}$, то $y=2x$. Все точки, для которых верна пропорция $\dfrac{x}{y}=\dfrac{1}{2}$, будут лежать на одной прямой, являющейся лучом решений.

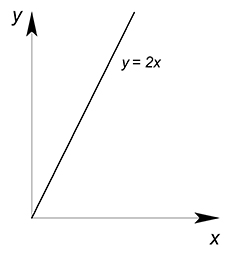
Как известно, эффективная точка будет лежать на границе производственных возможностей. Одновременно он будет принадлежать лучу решений. Найдем её:

$y=\sqrt{100-x^2}=2x$

Из уравнения находим $x$ и соответствующий ему $y$:

$x=2\sqrt{5}$

$y=4\sqrt{5}$

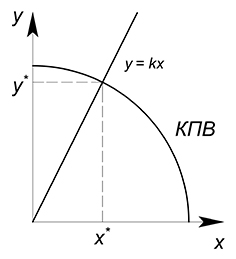
В общем виде:

КПВ:

$y=f(x)$

Пропорция производства товаров:

$y=kx$

Отсюда находим $x$ и $y$