В стране Скуфиляндия существует одно единственное озеро где водится здоровый карась. Группа из рыбаков решает поделить озеро для рыбалки. Для этого они чертят схему озера: окружность диаметром 40 см. Затем каждый по очереди чертит окружность диаметром 20 см - место, где он будет рыбачить на своей лодке. Окружности могут лишь касаться, но не накладываться друг на друга; заходить за край озера можно, если центр окружности внутри озера и не нарушено первое условие. Рыбак, который не может начертить окружность, не рыбачит.

Рыбаки знают, что полезность от размещения можно найти по формуле: $u(x_i,y_i)=20 - \sqrt{(20-x_i)^2+(20-y_i)^2}$, где $(x_i, y_i)$ - координаты центра окружности i-го игрока в евклидовом пространстве.

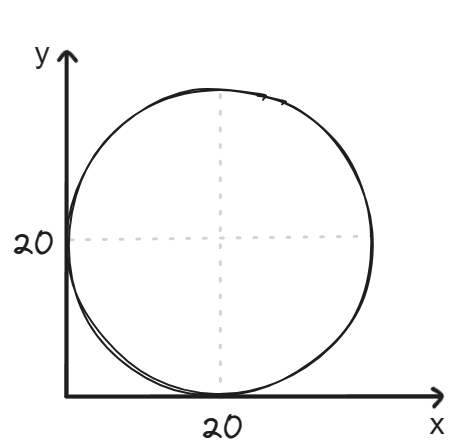
1) Рассчитать полезность для 2х рыбаков;

2) Найти максимальное количество рыбаков, которые смогут рыбачить. Если каждый из них будет рациональным (то есть стремиться максимизировать свою функцию полезности).

Взять $\pi = 3,14$