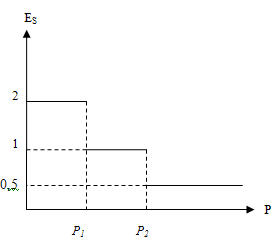
На рынке три группы производителей, каждая из которых характеризуется отличной от других функцией предложения: первый продавец готов продавать начиная с цены 0 рублей, второй – готов продавать не ниже $P_1$, а третий – не ниже $P_2$, причем каждая функция непрерывна и не имеет «изломов». Может ли график эластичности рыночного предложения по цене иметь следующий вид при условии выполнения закона предложения?

Комментарии

test user
07.09.2010 14:21    
Есть информация, что г-н Хацевич к этой задаче не имеет никакого отношения.
Данил Фёдоровых ↑
06.04.2008 16:26    
Да? Ну ладно. Найдете автора — сообщайте :-)
Дмитрий Сорокин
27.01.2009 19:49    
А можно ли сослаться на то, что функция $Q_S^2$ существует при цене больше 0, а по условию должна существовать при цене большей $P_1$?
Данил Фёдоровых ↑
27.01.2009 22:09    
А разве это не зависит от $a$ и $b$? Например, если $a=1, b=P_1$, то $Q_S^2>=0$, вроде бы, там, где надо.
Дмитрий Сорокин
27.01.2009 22:58    
1) Ну $P_1$ попадет на убывающую ветвь))))Нет, ну при Р, стремящемся к 0, он будет поставлять на рынок положительное Q, а это значит, что функция предложения опеределена в окрестностях 0, хотя по условию он продает при цене большей 0.
Данил Фёдоровых ↑
28.01.2009 04:27    
А, сорри, я сначала неправильно понял, о чем вы спрашиваете. Да, вероятно, такая ситуация не могла сложиться и по приведенной вами причине.
Алексей Суздальцев
28.01.2009 15:36    
Из решения следует, что функция предложения второй группы производителей равна $Q_s=aP-bP^2$ при ценах больших, чем $p_1$и нулю при всех $P

Дмитрий Сорокин
28.01.2009 22:47    
Но ведь тогда эта функция не является непрерывной! =)
Алексей Суздальцев
28.01.2009 23:21    
Существуют такие $a$ и $b$, что эта функция является непрерывной.
Михаил Сметанин
24.10.2013 10:14    
Правда ли, что на участке [0, p2] - функции могут существовать? То есть они могут быть непрерывны, но определены только на этих отрезах.

И все "портит" только третья функция, определенная на луче? То есть если в условии третий участок был [р2,р3] то ответ был бы "да"?

Сергей Кравченко ↑
25.10.2013 22:32    
Миш, если при такой формулировке ты считаешь правильным ответ «да», тебе всего лишь нужно привести пример таких a, b и с)