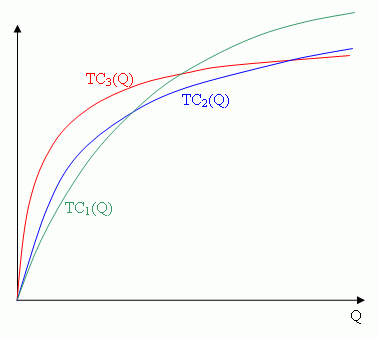
Три коалы Мэри, Вано и Жозефина заготавливают траву и продают её на экспорт. У каждого коалы своя функция издержек; все они втроём изображены на рисунке.
Когда коалы хотят произвести Q единиц продукции, они распределяют работу между собой так, чтобы минимизировать суммарные издержки. Так получается функция суммарных издержек всей их коалиции $TC(Q)$.
Изобразите на данном рисунке функцию $TC(Q)$ как можно более точно.

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ
Комментарии
Но не нужны забывать что еноты - хитрые ребята. Как мы видим, у каждого енота нет $ TFC $. Тогда суммарный $ TC $ от некоторого выпуска $ Q' $ нужно сравнить с $ TC_1(Q');TC_2(Q');TC_3(Q') $. Если суммарные издержки будут меньше - это то, что нужно. Если больше - нужно проверить такие объёмы производства, что 2 завода производят, а один "стоит без дела", т.е. всего ещё 3 варианта (производят 1;2 и 2;3 и 1;3) и с последними тремя вариантами, что один завод производит, а два остнутся без дела (которые я уже упомянул выше). Вроде, это полный перебор.
я думаю ты имелл ввиду $ MC_1(Q_1)=MC_2(Q_2)=MC_3(Q_3) $, причем $ Q_1+Q_2+Q_3=Q_* $
Может просто горизонтально TC суммировать?))
понятно что мы некоторое время красным енотом не будем пользоваться вообще ^^
у него дикие $ TC $ при малых $ Q $
Гриша, решение через множество касательных может считаться решением?
Поднажмите, ребята, мы тут уже тремя способами решили, один красивее другого:)
сначала берем зеленый участок..до пересечения с синим,
потом синий до пересечения с красным, ну и наконец красный
в общем получится $TC$ из трех участочков
это лишь догадка..но по-мойму похожая на правду)
потом начинает полностью синий работать и красный так же, тогда участки как раз такими будут
Значит, заметим, что от совмещения производств выгоды нет, т.к. все функции издержек отвечают убывающим MC, значит при каждом Q мы просто будем выбирать те затраты, которые меньше чем на каждом из 2х других заводов, поэтому можно обвести на каждом участке нижний из графиков TC.
я думал как же это написать про убывающие MC
я думаю это решение..а вообще очень сложно обсуждать эту задачу в письменной форме
В общем за такую идею я обеими руками за)
Если мы хотим пожертвовать некоторыми издержками для снижения MC в будущем, то комбинирование производств нецелесообразно так как если мы на одном заводе сколько-нибудь произвели, то для достижения нужного уровня MC на "свежем" заводе потребуется больше затрат, чем если бы мы на этом заводе начали производство.Вроде так.
Если же сейчас предельные издержки на первом ниже, чем на втором, то та же логика докажет, что выгодно перекинуть всё производство со второго на первый.
Я тебя правильно понял?
Я ведь пытаюсь тоже самое доказать, но захожу со стороны математики.
В общем, я о том, что возможен такой случай предельных издержек в случае, если у общих издержек >1 точки пересечения.
Если я пояснился, как обычно, очень коряво, то попытаюсь написать по - другому =)
Я просто не уверен, поэтому и спрашиваю. Хотел в общем виде более - менее довести задачу, понять как решать, если столкнусь с чем - то усложнённым.
А в чём общий вид? В данной задаче MC тоже пересекаются друг с другом
Те же рассуждения, только если две кривые MC по - очереди оказываются внизу, т.е. в некий момент образуют, например, участки синусоиды и косинусоиды на одинаковых интервалах, то это рассуждение про перенос производства будет немного более комплексным.
Или я опять..кхм. молодец?
Ну ладно, если суммарный объём зафиксирован, тогда как мы будем рассматривать множество точек (суммарные издержки, суммарный объём)? На данном графике, вроде, теперь понятно, мы по одной МС едем в одну сторону, а по другой - в другую. Но, по идее, это и есть общий случай, ведь две убывающие функции могут пересечься не более одного раза при условии что они не совпадают. Не знаю, надо ещё подумать над задачей. Вдруг у нас какой - то такой "хитрый вид" предельных издержек...
Но всё равно, Гриша, большое спасибо, что помог разобраться!
Ну и догмы у тебя:) контрпример
В общем, я понял, что я имел ввиду, и что я хотел сказать фразой "две убывающие функции могут пересечься не более одного раза при условии что они не совпадают" =))
Кстати, квазивыпуклая функция - это у которой для любого $x_0$ множество всех таких x, что $f(x)\le f(x_0)$, является выпуклым. Например, $f(x_1,x_2)=x_1^2+x_2^2$ (кривые безразличия вогнуты).
А "тождественные преобразования функции" - это вообще для меня что-то новое.
открывая второй завод с целью уменьшения $MC$ в будущем нам выгоднее полностью перенести производство с первого на второй, так как чем больше $Q_2$ тем меньше $MC_2$ и все от больших $MC_1$ отказываемся
У нас с Димой разные подходы =)
делаем так, до пересечения зеленого и синего работает ТОЛЬКО зеленый
если мы хотим произвести больше чем Q=пересечению зеленой и синей ТС, то производит ТОЛЬКО синий
если хотим произвести больше чем Q=пересечению синей и красной, то производит ТОЛЬКО красный
таким образом при каждом Q я просто выбираю самый нижний участок ТС и произвожу все на нем, ну и получаю ТС из трех участков, сначала зеленый, потом синий, а потом красный
Но, похоже, мой замечательный решатель задач где - то обсчитался.. (В данном случае я подразумеваю себя).
Я придумал функции $ y(x) $, которые имет вид как у тебя. Далее нарисовал по точкам с очень маленькими делениями по оси $ Ox $. Далее подбирал значения $ x_1;x_2;x_3 $ такие, что функция $ f(x_1;x_2;x_3) = y_1(x_1)+y_2(x_2)+y_3(x_3) $ была как можно более вогнутая, т.е. при $ f(x_1;x_2;x_3) = const $ некоторая функция $ g(x_1;x_2;x_3)=x_1 + x_2 + x_3 = X \longrightarrow max $ по $ {x_1;x_2;x_3} $.
update: как писать максимизацию по некоторым переменным? Т.е. как в tex-e оформить ->max и под max подпись по каким переменным я максимизирую функцию?
во-первых под словом дальше я имею ввиду увеличение Q
начнем с первого участка, заметим что MC минимально на зеленой ТС, значит начнем производство именно с зеленой, далее докажем что до пересечения с синей ТС будем производить только на зеленой.
ну это понятно, $ MC_1
ну так значит так
См. также вторую часть вот этого комментария к задаче "На внутреннем и внешнем рынках - 2".
P.S. Если объяснил непонятно - пишите, объясню подробнее.
С этим ты согласен?
Тангенс угла наклона секущей к графику $TC_i$ есть $AC_i$. Раз $AC_i$ убывают, то, когда мы увеличим выпуск на i-м заводе, они и убудут.
Про сравнение с единицей что-то сомнительное ты написал. Если не найдёшь ошибку в доказательстве, пиши его сюда.
Ну я имел ввиду ту часть, где вы пишите, что если у нас есть некоторый завод, дающий $ AC_{i}(Q_{i}) $, наименьший из всех средних издержек, и есть другой завод $ AC_{j}(Q_{j}) $ с ненулевым выпуском $ Q_{j} > 0 $, то если мы перекинем весь выпуск со второго завода на первый, то получим $ AC_{i}(Q_{i} + Q_{j}) < AC_{i}(Q_{i}) $. В случае, если тангенс укла секущей к графику $ TC_{i} $ убывает (как тут), то вроде всё вышесказанное верно, а если не убывает? Мне просто было интересно, подойдёт ли это решение для общего случая?
Т.е. прикол получается в том, что .. Не знаю как нормально сказать. Что $ \Delta TC = TC_{i}(Q_{i} + Q_{j}) - TC_{i}(Q_{i}) $ могло вырасти в большей степени, чем $ \Delta Q = Q_{j} $. Тогда и $ AC_{i} $ возрастут.
Спасибо)