3.6 Производственная функция

Фирма производит свою продукцию, следуя определенной технологии.

Производственная функция показывает налучшую технологическую зависимость между количеством используемых ресурсов и объемом выпуска.

$Q=f(L;K)$

Из производственной функции можно вывести функцию издержек.

Пример 1
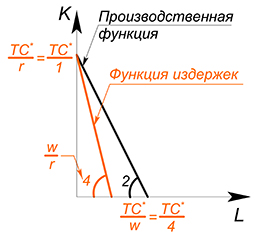
Дано: $Q= L \cdot K$, $w=4$, $r=1$, найти функцию общих издержек.

В данном случае можно или минимизировать издержки при выбранном уровне $Q$, или максимизировать объем выпуска при данном уровне издержек.

Воспользуемся методом 2:

$TC=wL+rK$

$TC=4L+K$

Как уже не раз случалось, мы опять встречаем функцию, зависящую от двух переменных. Зафиксируем $TC$, выразим $L$ через $K$:

$K=TC^*-4L$

Что касается производственной функции - зафиксируем $Q$, выразим $L$ через $K$:

$K=\dfrac{Q^*}{L}$

Имеем схожую ситуацию с задачей максимизации полезности, только в данном случае у нас цель - максимизировать объем выпускаемой продукции:

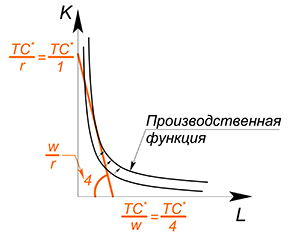
Возьмем производную обеих функций по $L$, найдем точку, в которой они равны, найдем точку касания графиков

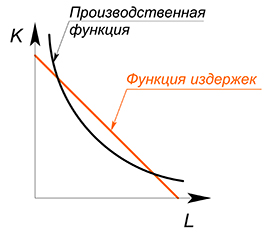
(Почему именно касания? Если бы мы выбрали более низкий уровень $Q^*$, то мы получили бы более низкую производственную функцию, произвели бы меньше продукции с теми же издержками:

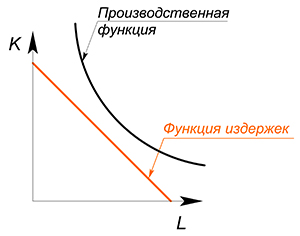
Если мы бы выбрали слишком высокий уровень $Q$, то данный объем производства был бы недостижим при данном уровне издержек:

$-4=-\dfrac{Q^*}{L^2}$

Выразим $L$ ($L>0$):

$L=\sqrt{\dfrac{Q^*}{4}}=\dfrac{\sqrt {Q^*}}{2}$

Подставим в производственную функцию, выразим $K$:

$K=2\sqrt{Q^*}$

Теперь подставим $L$ и $K$ в функцию издержек, $Q$ снова является переменной:

$TC=\dfrac{4\sqrt{Q}}{2}+2\sqrt{Q}=4\sqrt{Q}$

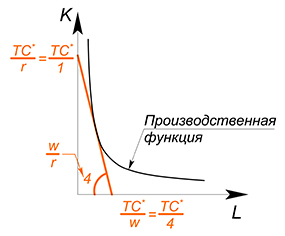Пример 2
Производственная функция является линейной: $Q=2L+K$, $w=4$, $r=1$, $TC(Q)-?$

Действовать будем в целом аналогично предыдущему варианту, но в этот раз попробуем использовать метод 1: будем минимизировать издержки при выбранном уровне $Q$:

$TC=4L+K$

$K=TC^*-4L$

$K=Q^*-2L$

Имеем 2 линейные функции, будем двигать функцию издержек вниз, пока она не достигнет оптимального положения:

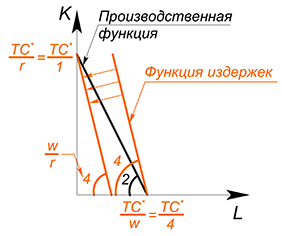
(Если мы выберем более высокий уровень издержек, то вступим нерационально - такой же объем выпуска при больших издержках. Зачем? Если выбрать более низкий уровень издержек, то невозможно будет произвести нужный объем продукции) .

Оптимальное положение будет достигнуто в точке, где количество капитала максимально, а труда равно нулю. Тогда:

$Q=K$

$TC=K$

$TC=Q$

Эффект масштаба показывает во сколько раз изменится $Q$ после увеличения всех используемых ресурсов в одинаковое число раз $t$ по сравнению с первоначальным $Q$, увеличенным в $t$ раз.

$Q_{новое}(tL;tK)$ vs $tQ(L;K)$

Если $Q_{новое}(tL;tK) > tQ(L;K)$, то эффект масштаба положительный, если $Q_{новое}(tL;tK)=tQ(L;K)$, то постоянный, если $Q_{новое}(tL;tK) < tQ(L;K)$, то эффект масштаба отрицательный.

Пример 3
$Q=4L+K^2$, какой эффект масштаба наблюдается в данной ситуации?

$(tK)^2+4tL$ vs $t(K^2+4L)$

$t^2K^2+4tL$ vs $tK^2+4tL$

$t^2$ vs $t$

$t>1$, следовательно эффект масштаба положительный

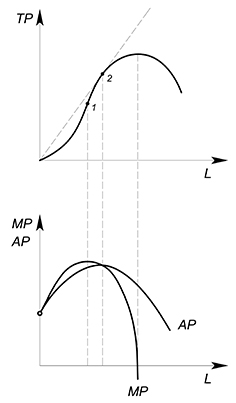
TP - total product (он же Q), общий продукт труда - показывает зависимость объема выпуска продукции от количества переменного ресурса при прочих равных условиях.

Функция $TP$:

i участок - функция растет ускоряющимся темпом, при найме каждого последующего работника объем выпуска увеличивается на все большую и большую величину;
ii участок - функция растет замедляющимся темпом, при найме каждого дополнительного работника объем выпуска увеличивается на все меньшую величину;
iii участок - $TP$ убывает. При производстве товара может наступить такой момент, когда дополнительная единица переменного ресурса (труда обычно) уже не способствует увеличению производимой продукции. Дополнительно нанятый работник может только мешать. Например, если у нас имеется всего один станок, и мы наняли 50 рабочих, то они будут только мешать друг другу, стопившись у этого единственного механизма.

$AP_(L)$ average product, средний продукт (труда) - показывает, сколько в среднем единиц продукции приходится на одну единицу переменного ресурса:

$AP_L=\dfrac{TP}{L}$ (бывает $AP_K=\dfrac{TP}{K}$)

$AP_L(L)=\dfrac{TP(L)}{L}$

Геометрический смысл среднего среднего продукта труда такой же как и у других средних величин - тангенс угла наклона луча, проведенного из начала координат (секущей) к точке на графике общего продукта труда.

$MP_(L)$ - marginal product, предельный продукт (труда) - показывает прирост общего продукта при увеличении переменного ресурса на единицу.

В дискретном случае $MP_L=\dfrac{TP_2-TP_1}{L_2-L_1}$.

Геометрический смысл предельного продукта в данном случае - тангенс угла наклона секущей, соединяющей точки $(L_1;TP_1)$ и $(L_2;TP_2)$.

Если ресурс бесконечно делим, то $MP_L=TP'(L)$

Геометрический смысл предельного продукта в этой ситуации - тангенс угла наклона касательной, проведенной к графику $TP$ в интересующей нас нас точке.

Пример 4
$Q(L)=30L-L^2$, найти $AP_L$, $MP_L$

$AP_L=\dfrac{Q(L)}{L}=30-L$

$MP_L=Q'(L)=30-2L$