Задача
Темы
Сложность
(1 оценка)
Автор
(0)
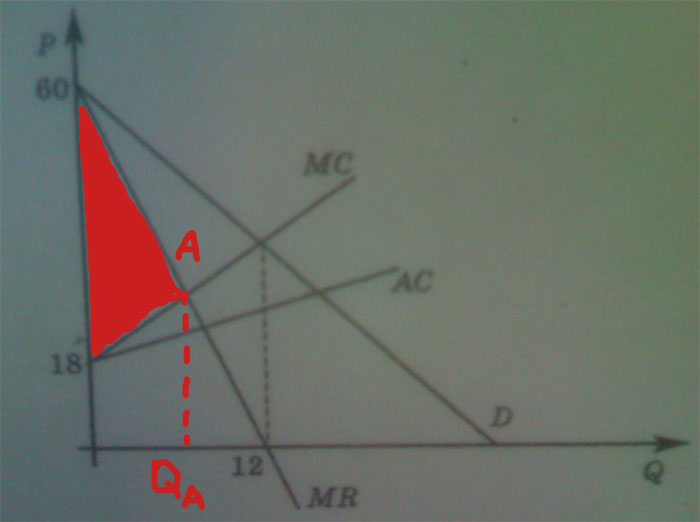
Фирма, являющаяся монополистом на рынке товара М, максимизирует прибыль. Информация о спросе (D), предельной выручке (MR), предельных (МС) и средних (АС) издержках представлена на рисунке (перечисленные функции линейны).
1. Определите максимальную прибыль монополиста.
2. Изобразите ее на графике


 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ
Комментарии
1. Для монополиста кривая спроса в 2 раза положе, чем предельная выручка, то есть примерно там, где у вас стоит точка D (хотя в реале это не точка, а кривая спроса). Короче говоря, там, где кривая спроса пересекает ось количества Q = 24. Отлично, теперь у нас есть две точки, а этого достаточно, чтобы вывести кривую спроса. Пишем Qd=a-b*P и подставляем две пары координат (0;60) и (24;0) - находим уравнение кривой спроса. Qd=24 - 0.4*P
2. Теперь выведем уравнение MC. Нам снова нужны две пары координат: одна есть (0;18). Найдем вторую. Видим на оси количества точку Q = 12 - подставляем ее в функцию спроса и находим P = 30. Аналогично первому пункту выводим уравнение кривой MC. Получается: MC = 18 + Q
3. Выведем уравнение MR - можно через 2 точки, а можно из экономических соображений - график MR в два раза круче спроса. В итоге получается: MR = 60 - 5Q.
4. Максимизируем прибыль: MR = MC, то есть 60 - 5Q = 18 + Q, получаем оптимальный объем Q = 7
5. Считаем прибыль. Pr = TR - TC. С выручкой все ясно при объеме Q=7 цена будет P = 42.5, то есть TR= 297.5. Найдем TC как интеграл от MC: TC = Q^2/2 + 18Q. Посчитаем TC(7) = 150.5. И получим прибыль 147.
На графике: Находим пересечение MR и MC - это и будет оптимальный объем выпуска - опускаем перпендикуляр на ось количества зрительно вычитаем площадь под графиком MC из площади под графиком MR. Закрашенный треугольник - и есть результат этого действия. Он то и равен максимальной прибыли. Вроде все. А, ну и рисунок.
Видно, что AC(0) = 18 и линейно возрастает. Тогда TFC = 0. Ну а раз так, то поделим коэффициент при Q в MC пополам ты получишь функцию АС.
Но тогда в пункте 2 нечего писать будет :)
$\lim_{Q{\to}0}{\frac{TC}{Q}}=\lim_{Q{\to}0}{\frac{FC}{Q}}+\lim_{Q{\to}0}AVC<+\infty$
Но если мы подставим $ Q = 0 $ в формулу $ АС = ТС/Q $, то получим непонятную штуку. Или вполне понятную: надо её раскрыть по правилу Лопиталя и будет то, что нужно?
В данном случае, если FC будет больше нуля, то АС будет очень большой величиной при маленьких выпусках, что противоречило бы представленному графику.
понять не могу.
значит MR=a-2bQ,b-это коэффициент наклона,они отличаются только тем что у одной фунции b,а у другой 2b
поэтому обр функция спроса в два раза круче.
Съезди - разберись, тебе близко :)
Могу пояснить через прямоугольник. Нашли оптимальный объем и находим, какие будут средние издержки и цена спроса при этом объеме. Далее, пишем формулу Pr = Q*(P-AC) и закрашиваем ту фигуру, которую она обозначает - это и будет тот самый прямоугольник.
Хотелось бы узнать, почему через треугольник неверно?
http://iloveeconomics.ru/zadachi/z475#comment-5873
ААА, вроде дошло, если FC > 0, то AC = VC/Q + FC/Q - дробно-линейная (или, по крайней мере, точно не линейная) зависимость. Так (учитывая, что FC = a, где а - число)?