Два школьника решают задачи и тесты, у каждого из них есть по одному часу времени.
Первый школьник решает задачи со скоростью 3 задачи в час, а тесты - со скоростью 1 тест в час.
Второй школьник решает задачи со скоростью 1 задача в час, а тесты - со скоростью 3 теста в час.
Но это - если они решают отдельно друг от друга. Если же они садятся решать вместе, то задачи они решают со скоростью 5 задач в час, а тесты - со скоростью 5 тестов в час.
Время они могут делить как угодно: например, сначала вместе полчаса порешать задачи, а затем первый свои оставшиеся полчаса самостоятельно решает задачи, а второй 15 минут самостоятельно решает задачи, а 15 минут самостоятельно решает тесты.
Первый школьник решает задачи со скоростью 3 задачи в час, а тесты - со скоростью 1 тест в час.
Второй школьник решает задачи со скоростью 1 задача в час, а тесты - со скоростью 3 теста в час.
Но это - если они решают отдельно друг от друга. Если же они садятся решать вместе, то задачи они решают со скоростью 5 задач в час, а тесты - со скоростью 5 тестов в час.
Время они могут делить как угодно: например, сначала вместе полчаса порешать задачи, а затем первый свои оставшиеся полчаса самостоятельно решает задачи, а второй 15 минут самостоятельно решает задачи, а 15 минут самостоятельно решает тесты.
Требуется построить их совместную кривую производственных возможностей (для каждого возможного количества решённых задач она показывает, какое максимальное количество тестов они смогут решить).
Задачи и тесты предполагаются бесконечно делимыми:)

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ
Комментарии
КПВ для определённого кол-ва времени или выраженно всё в t будет?
Т.к. товары абсолютно идентичны, то можно нарисовать кпв только на 45 градусов, а потом просто сделать такую - же на второй половинке. Т.е. если провести биссектриссу угла, то мы можем нарисовать кпв в одной половине и перерисовать на другую.
Тогда получится, что кпв проходит через точки (5;0) ; ($\frac{27}{7}$;$\frac{15}{7}$); (3;3)
UPDATE Это решение - наглое враньё.
Перейдёт же их совместная работу в раздельную тогда, когда кривые пересекутся. Т.е. y=5-$\frac{4x}{3}$=4-$\frac{x}{3}$, откуда x=1.
Тогда КПВ (5;0), ($\frac{11}{3}$;1) и (3;3). Я обсчитался в прошлый раз.
Ладно, в общем. Какие 4/3?
Даня, ну поясняй, не понятно же нифига! Что это за кривые, какими формулами задаются и т.д.
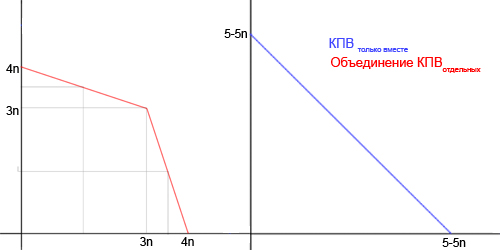
красная - КПВ
коричневая - суммарная кривая КПВ без фишки с увеличением производительности. По - хорошему, в точке (3;3) она должна загнуться, но я это не прорисовал.
зелёная - суммарная КПВ с совместным производством. Кусок общей КПВ(красной жирной линией) покрывает частичку зелёной. Рассматриваем точку, где Q1=4. Т.к. они сначала будут производить вместе, а потом только тот, у кого в производстве данного продукта меньше производительность, будет доделывать оставшееся время оставшуюся часть продукта. Находим, что при уже упомянутом Q=4 tсовместной работы=3/4. Значит, получаем точку (4;0,75). Далее доказываем, что в интервале до пересечения кривой с объединением с кривой без объединения труда, кривая с объединением труда имеет линейный вид. Тогда записываем уравнение прямой кпв с объединением. Q1=5-Q2/0,75. Также для кпв без объединения: Q1=4-Q2/3. Находим точку пересечения. Строим симметричное её отражение относительно прямой, явлюящейся биссектрисой угла, образованного осями с продуктами. Получаем данную кпв. Всё! :)
Оттуда, вроде, и 4/3 появляется (угол наклона кпв с объединением).
Далее придумываем экономическое решение (я пока в процессе) =)
Напишу вкратце смысл решения, если верно, дополню подробностями.
В общем так, строим сначала объединение КПВ для того случая, если они работают по отдельности. Эта кривая отражает максимально возможное совместное производство при раздельном труде.
Второй этап - на том же графике строим КПВ для случая совместной работы.
Ну и собственно обводим ту часть каждой из кривых, что лежит выше другой.
Математически это чем-то напомнило мне применение знака совокупности.)
Подошел немного по-другому к задаче, получилось другое КПВ, но метод решения весьма странный, поэтому, для начала итог решения:
Пусть $1-n$ - количество времени, которое школьники тратят
на совместную работу, $n$ выражено в долях часа, $z$ - количество задач, $t$ - количество тестов.
Тогда
$\frac{z}{5}+\frac{t}{5}=1-n$ - совместная кпв(1)
Соответственно каждый школьник на собственные занятия потратит $n$ времени
Т.е.
$\frac{z}{3}+t=n$ - индивидуальная кпв первого при работе отдельно(2)
$z+\frac{е}{3}=n$ - индивидуальная кпв второго при работе отдельно(3)
Теперь изобразим объединение КПВ для отдельной работы(2+3) и КПВ(1).
Теперь, так как эти КПВ учитывают разделение времени на работу совместно и раздельно. Мы можем их объединить.Получим следующее:
Из данной обобщенной КПВ извлечем две системы:
$\begin{cases} z=5-2n\\t=3n\end{cases}$
$\begin{cases} z=3n\\t=5-2n\end{cases}$
При условии $n\le1$ тогда выполняется:
$t=5-\frac{2}{3}z$
$z=5-\frac{2}{3}t$
Получаем в итоге следующий график:
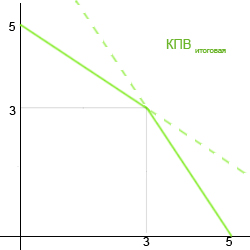
На графиках я не подписал оси, однако это не вносит никаких изменений, так как условие симметрично относительно $z$ и $t$.
Рассмотрим сначала случай $z\le3$. Докажем, что максимальное значение t будет на той кпв, при которой мы окажемся в левой точке излома (то есть при таком n, что z=3n, t=5-2n). Представьте, что мы нарисовали только что описанную кпв. Выгодно ли нам менять n? Если мы увеличим n, то верхний красный участок начнётся из точки с меньшей вертикальной координатой, и поэтому, глядя на форму кпв, мы понимаем, что при старом z соответствующее значение t будет меньше, то есть увеличивать n невыгодно. Выгодно ли уменьшать n? Если уменьшить n (скажем, на величину $\delta$), что старому значению z=3n будет соответствовать синий участок, а значение t в точке z=3n будет равно $5-2(n-\delta)-3n=5-2n+(2\delta-3n)$. Поскольку $\delta$ - это то, насколько мы уменьшили n, то $\delta\le n$, и поэтому $2\delta-3n<0$, то есть мы теперь имеем меньшее t, чем раньше. Итак, уменьшение n невыгодно.
Случай z>3 рассматривается симметрично (нужно поменять оси местами).
Только вот я чего - то затупил, а как нам достичь производства (4;1,5)?
Пусть, нам НАДО решить $ х $ задач. Решая эти $ x $ задач они работают только вместе и тратят на это $\frac{1}{t}$ часов. Рассмотрим точку, лежащую на прямой x=5-y. Она нам даст некий результат $ y $. Далее, будем "оптимизировать" этот результат. Очевидно, мы можем это сделать только если ребята начнут заниматься по одиночке какое - то время. Предположим далее, что ребята будут тратить на решение задач не $\frac{1}{t}$, а $\frac{2}{2t+1}$. Тогда, чтобы сохранить тот же объём решенных задач, одному из них придёться "догнаться задачами" в одиночку, в то время как второй "размочит" счёт по отношению к сделанным тестам. Далее, когда $ x $ задач будет решено, они продолжать вместе делать тесты.
Теперь рассмотрим, кому же из них будет выгоднее "догоняться задачами". Пусть первый из них быстрее решает задачи. Получится же, что если первый догоняется задачами, то он сделает это в 3 раза быстрее, и они в 3 раза быстрее начнут вместе решать тесты, ежели это будет делать второй паренёк. Очевидно, тесты совместно им решать оптимальнее всего, т.к. их "тестовая" производительность наибольшая. Сравнив "тестовые" потери придём к выводу, что первому чуваку лучше всего дорешать оставшуюся часть тестов (можно рассмотреть частный пример, т.к. АИ постоянны, то это не имеет значения. Т.е. если они решали 3,5 задачи и делали 1,5 теста (точка на совместной КПВ), то они тратили на совместное решение задач $\frac{3}{10}$часа. Теперь рассмотрим, что совместное время решения задач будет равно $\frac{6}{21}$. Если 2 парень доделывает задачи, то он потратит на них ещё $\frac{1,5}{21}$ часа, и общее число тестов будет равно $\frac{1,5*3+13,5*5}{21}$=$\frac{72}{21}$=3,4286. Продолжив так делать, т.е. устремив $ t $ к бесконечности, получим 3,5 сделанных теста. Если же сделать наоборот, когда первый парень будет доделывать задачи, то получим кол-во тестов равное $\frac{0,5*3+14,5*5}{21}$=$\frac{74}{21}$=3,5238. При $ t $ -> бесконечности $ y $ ->4.
Можно же доказать в общем виде, что первому дорешивать задачи выгоднее. Исходя из того, что он потратит на это в 3 раза меньше времени, то другой успеет сделать в 3 раза меньше тестов. Но зато они в 3 раза раньше начнут совместно решать тесты с максимальной производительностью. Поэтому так будет продолжаться до $ t \ge \frac{3}{5} $, а это и есть точка (3;3).
Представь, что ты построил суммарную кпв из нескольких индивидуальных кпв (стандартная задача), а потом тебе ткнули в точку на кпв и спросили, кто что в ней делает. Ты ведь легко ответишь на этот вопрос, идя по какой-нибудь из осей от нуля до выбранной точки. Мы сейчас сделали ровно то же самое, просто в качестве третьего "работника" мы используем их совместный труд и соответствующую кпв.
Для любой другой точки с з>3 рассуждения аналогичны, а для точек с з<3 меняется только то, что совместно они уже будут делать не задачи, а тесты (т.к. мы теперь на левой точке перелома красно-синей кпв).
Но всё это не тот способ, который я подразумеваю. Наверное, нехорошо заставлять решать уже решённую задачу другим способом, поэтому я разместил отдельную задачу.