Задача
Раздел
Темы
Сложность
(2 оценок)
Автор
08.01.2010, 13:27 (Григорий Хацевич)
26.05.2015, 17:25
26.05.2015, 17:25
Следующий схематичный рисунок описывает некоторую совершенно конкурентную фирму:
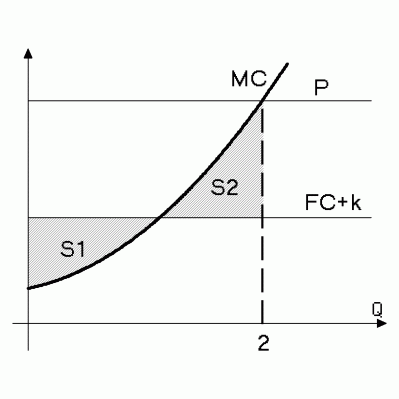
Найдите её прибыль, используя следующий набор в разной степени полезных фактов:
TC непрерывна
$FC=\frac{S1-S2}{2}$
$k=P-2FC-2$
$MC'(3)=10$
$\int\limits_1^2 AVC(Q)dQ=3$
$\lim\limits_{Q\to 0}AC(Q)=2$
Факультет экономических наук НИУ ВШЭ
Комментарии
Вообще тема долгосрочного периода довольно непростая, и заслуживает отдельного подробного обсуждения. Я напишу подробно на эту тему, когда сам с ней хорошенько разберусь:)
$\lim\limits_{Q\to 0}AC(Q)=2$
$\Updownarrow$
$\lim\limits_{Q\to 0}FC/Q + AVC(Q)/Q=2$
Если $FC\neq0$, то $\lim\limits_{Q\to 0}FC/Q + VC(Q)/Q=\infty$
$\Updownarrow$
$FC=0$
$S_1=S_2$
Тогда площадь фигуры ограниченной P;MC и осью координат, равная величине прибыли, равна площади $$S=2\cdot (P-(FC+k))=2\cdot(\underbrace{P-k}_\mathtt{=P-k-2FC=2})=2\cdot2=4$$
Думал про односторонние, двусторонние, разрыв... видимо "непрерывность" ?
Я использовал его в решении, правда мое решение более длинное, чем у Тимура.