Задача
Темы
Сложность
Голосов еще нет
Автор
27.02.2012, 21:00 (Григорий Хацевич)
27.02.2012, 21:27
27.02.2012, 21:27
(0)
У Дяди Фёдора удивительная корова: вместо молока она даёт бесконечно делимые коровьи рога.
Производственный процесс устроен следующим образом:
1. Дядя Фёдор говорит своей корове, какое количество рогов Q он хочет получить от неё сегодня;
2. корова отвечает, какой объём травы ей нужно употребить, чтобы она могла дать столько рогов;
3. осуществляется обмен травы на рога.
Дядя Фёдор знает, как зависит ответ коровы от запрашиваемого количества рогов; если он просит у коровы Q рогов, то ему придётся купить травы на TC(Q) рублей.
Дядя Фёдор — монополист на рынке коровьих рогов. На рисунке изображён спрос на рога, а также график функции $AC(Q)=TC(Q)/Q$.
В каждом из следующих случаев определите графически, сколько рогов будет просить у коровы и продавать на рынке Дядя Фёдор, чтобы максимизировать прибыль.
а)
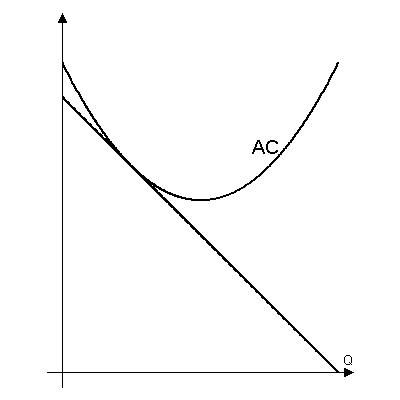
б)
Производственный процесс устроен следующим образом:
1. Дядя Фёдор говорит своей корове, какое количество рогов Q он хочет получить от неё сегодня;
2. корова отвечает, какой объём травы ей нужно употребить, чтобы она могла дать столько рогов;
3. осуществляется обмен травы на рога.
Дядя Фёдор знает, как зависит ответ коровы от запрашиваемого количества рогов; если он просит у коровы Q рогов, то ему придётся купить травы на TC(Q) рублей.
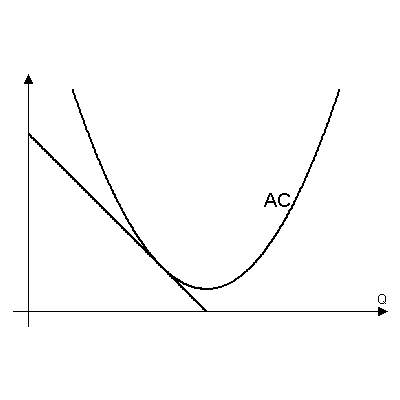
Дядя Фёдор — монополист на рынке коровьих рогов. На рисунке изображён спрос на рога, а также график функции $AC(Q)=TC(Q)/Q$.
В каждом из следующих случаев определите графически, сколько рогов будет просить у коровы и продавать на рынке Дядя Фёдор, чтобы максимизировать прибыль.
а)
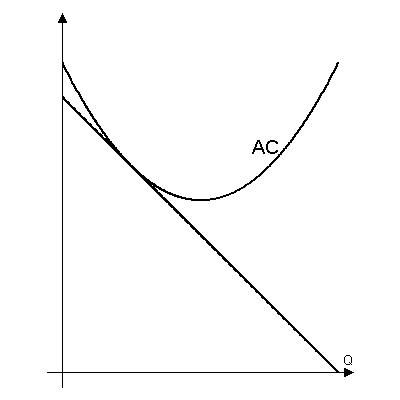
б)


 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ
Комментарии
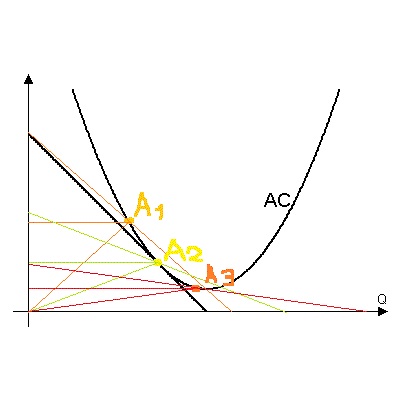
в б) при $E_{Q}^{AC}=-1$, построить такую точку можно следующим образом: проводить кривые вида $\frac{A}{Q}$, в точке касания $AC$ и такой кривой и будет единичная эластичность.
А можешь как-нибудь найти эту точку без компьютера?
Если $TC$ имеет убывающие участки ( а оно их имеет т.к $TR$ при $E^Q_P = -1$ больше, чем $TC$ в точке касания, а значит $TC$ при $Q (E=1)$ больше $TC$ в точке касания). Тогда это означает, что $MC$ пересекает ось $Q$ два раза (потому, что потом $TC$ опять возрастают). Тогда очевидно, что выгодно продавать не более чем количество соответствущее максимальной выручке, а покупать количество, то при котором $TC$ минимальны. Они минимальны, когда $MC$ пересекает ось $Q$ второй раз (т.к. вначале было доказано, что $TC$ уменьшились, а уменьшиться они могли только, когда $MC$ < 0. Значит нам выгодно будет производить до тех пор, пока $MC$ опять не станет положительными). Значит в точке оптимума $MC$ = 0. Следовательно наклон $|AC'| = |\frac{MC(Q_1) - AC (Q_1)}{Q_1}| = \frac{AC(Q_1)}{Q_1}$. И поэтому в точке, где $MC = 0$ должно, как Петя писал выше, выполняться касание кривой $\frac{A}{Q}$ и $AC$. Можно ли пользоваться тем, что $Q^d_{max}$ равен минимуму $AC$ и что угол наклона спроса $-1$? Или это случайность?
2) "Тогда очевидно, что выгодно продавать не более чем количество соответствущее максимальной выручке, а покупать количество, то при котором TC минимальны." - Не очевидно: TC ведь сначала возрастают, прежде чем начать убывать; и может, прибыль будет ещё больше в какой-то точке на участке возрастающих TC (представь, что изменение TC на всём убывающем участке очень маленькое, а перед этим они сильно возрастали).
3) То, что $Q^d_{max}$ равен минимуму AC - это случайность, но можешь пользоваться, если это тебе как-то пригодится.
То, что наклон спроса равен -1, мы не можем утверждать, потому что масштаб по осям не подписан. Хотя ты всегда можешь перейти к другим единицам измерения, чтобы наклон был равен -1; так что и здесь можешь предполагать, что наклон равен -1, если это чем-то поможет.
Кстати, идею решения этой задачи я придумал по аналогии с одной задачей по молекулярной физике: площадь под графиком на P-V диаграмме пропорциональна температуре, а линии, соответствующие одинаковой температуре,(изотермы) как раз гиперболы.
Нужно указать конкретную точку на этом рисунке, а не просто описать её свойства.
Но это тоже неудобное построение.
Но строить касательные все равно довольно трудно. Можно поступить так:
1) Построить в "подозреваемую" точку на кривой AC секущую из начала координат;
2) Опустить проекцию на одну из осей;
3) Построить вторую точку, симметричную началу координат относительно этой проекции;
4) Провести прямую через получившуюся точку и "подозреваемую" точку
5) Если получившаяся прямая очень похожа на касательную, то все круто, а если нет, то повторить со следующей "подозреваемой точкой"
Например, здесь видно, что точка А3 очень похожа на искомую