Фирма, максимизирующая прибыль, является монополистом на внутреннем рынке. Внутренний спрос на ее продукцию формируют две группы потребителей, функции спроса каждой из которых являются линейными. Ценовая дискриминация между группами внутренних потребителей запрещена. На внешнем рынке фирма может продать любое количество продукции по фиксированной мировой цене.
Функция предельных издержек фирмы строго возрастает.
Известно, что цена на внутреннем рынке составляет 46 денежных единиц. Эластичность спроса первой группы покупателей в точке максимума прибыли равна (-23/17), а второй группы – (-23). При этом эластичность внутреннего спроса находится в интервале от (-3) до (-1,5). Объем экспорта составляет 5 тысяч единиц продукции. Используя данные графика предельной выручки от продажи товара как на внутреннем, так и на внешнем рынках, определите значение мировой цены. 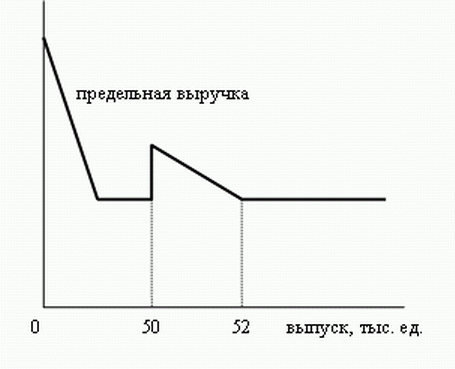

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ
Комментарии
О том, как найти задания олимпиады, написано здесь: http://iloveeconomics.ru/blogs/id324/165
Ну, в точке разрыва MR (Q=50) это определение будет относиться к пределу справа; а предел слева – это "сколько принесла продажа последней единицы ...". Во всех остальных точках пределы слева и пределы справа совпадают.
Общая выручка TR хоть и не дифференцируема в точке Q=50, но непрерывна во всех точках, поэтому в любой точке общая выручка есть площадь под нашим совокупным MR (в отличие от задачи "Непрерывность под прямым углом"). Например, считая таким образом площадь при $Q\in (50;52)$, мы учтём площадь под горизонтальным участком от y до 50, несмотря на то, что производя такое Q, мы совсем ничего не продаём на внешний рынок! Возможно, было бы более естественно в этом случае вместо площади под горизонтальным участком учесть сумму площадей двух трапеций. Но ведь эта сумма площадей как раз равна площади под горизонтальным участком (по построению точки Q=50), поэтому по большому счёту нам всё равно, каким из этих двух способов считать общую выручку. Но это при $Q\in (50;52)$. А вот при $Q\in (y;50)$ мы уже совершим ошибку, если вместо площади под горизонтальным участком будем считать площадь трапеций, т. к. получим выручку меньшую, чем на самом деле.
Пользуясь случаем, предлагаю обратить особое внимание на фразу:
Рассмотрим такой вопрос: "Пусть мы сначала продавали 49,99 единиц, а потом захотели увеличить объём продаж до 51. Насколько вырастет наша выручка?" Ответ – на $(51-49,99)\cdot w$, потому что весь прирост выпуска нам будет выгоднее продать на внешний рынок, а не как-то иначе (в этом можно убедиться, взглянув на рисунок из решения и дополнительно высчитав, что y=45, а x=48 – если я нигде не обсчитался). При этом было бы ошибкой, отвечая на этот вопрос, просто посчитать площадь под совокупным MR от 49,99 до 51, т. к. не выполняется предпосылка о том, что "все единицы до 51-й были проданы так (на тех рынках), чтобы максимизировать выручку от продажи 51 единицы": если мы уже продали 49,99 единиц на внешний рынок, то мы не можем на практике осуществить мысленный "манёвр", описанный в решении, т. к. мы не можем отобрать у покупателей с внешнего рынка эти 49,99 единиц, чтобы затем продать их на внутренний.
Зачем же нам нужен график совокупных MR? Он позволяет, совместив его с графиком MC, выбрать (совершенно стандартным образом – сравнивая площади) оптимальную точку, при условии, что мы ещё ничего не производили и не продавали.
Если да. То почему? Почему после верхней кривой спроса не идёт нижняя ? Ведь мы максимизируем MR?
Что-то я никак не врублюсь.
Максимизируем мы (выбирая, как распределить данное Q между рынками) скорее TR, а не MR.
1. Двигаясь по оси OQ, видим, что сначала MR убывает, а, так как на рынке совершенной конкуренции линия MR горизонтальна, то продажи есть только на внутреннем рынке. Проведем прямую AG через отрезок AB (все - на рисунке). Угол OGA - альфа. Как известно, линия предельной выручки в два раза круче линии спроса (для монополии). Значит, нужно построить угол 2 альфа.
Для этого отложим вправо от точки G по оси OQ отрезок, равный OG: GH = OG. Соединим точки A и Н, AH - спрос одной группы потребителей (той, у которой эластичность по модулю меньше - я этот вывод тоже опущу). Получается, зеленая линия - это спрос одной группы на внутреннем рынке (то что эта линия проходит через С, возможно, случайность, но строил я довольно точно (через фотошоп))
2. А вот дальше я не уверен в своих выводах еще больше, но все-таки напишу.
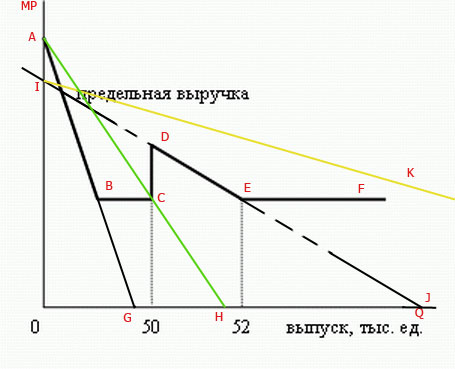
Мы видим, что следующий наклонный участок MR - это DE. Значит, проведем линию IJ через DE до пересечения с осями - это линия предельного MR, но, так сказать, экономически она существует только при Q>=50. Ну и строим спрос также как и прежде. Получается IK - кривая совокупного спроса. Но, я не могу правильно поставить на нее ограничение. И еще с этими маневрами немного запутался, но это отдельная тема. Вообщем, кто может, скопируйте мой рисунок и поверх него нарисуйте правильную кривую совокупного спроса на внутреннем рынке.
Построения спроса идейно верные, разве что рисунок тут схематичный (расстояние от 0 до 50 почти такое же, как от 50 до 52).
А зачем вообще рисовать кривую спроса?
Зачем рисовать спрос? Просто когда не знаешь с чего начать, нужно начать с начала. (на самом деле я просто по фотошопу соскучился :) )
И все-таки, может ты скажешь, какой вид на самом деле имеет кривая совокупного внутреннего спроса?
Можешь попробовать нарисовать MR точно (взяв цифры из решения), и восстановить тогда кривую спроса.
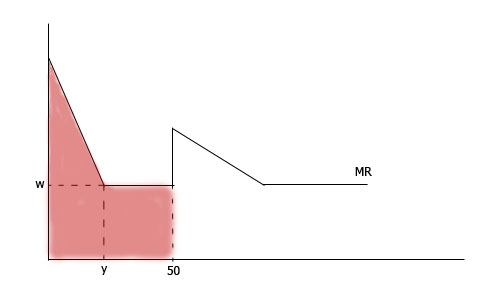
Нам нужно выразить TR. Графически это площадь под графиком MR. Тогда без маневра это будет вот так:
А с маневром:
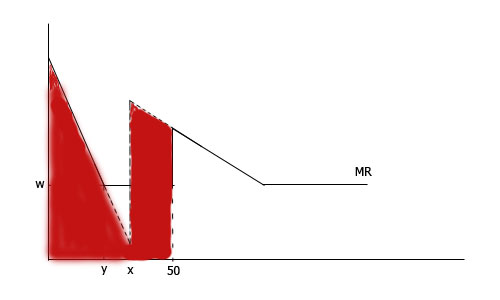
Насчет Y все понятно, но, по-моему, то что написано в решении не подходит для площадей вышеобозначенных фигур.
Кстати, есть одни вопрос, не по задаче. Допустим, что есть фирма монополист и известен ее спрос Q=a-bP, а также MR = c. И нам нужно найти объем, максимизирующий выручку. Почему нельзя делать так: MR = TR` = (aP - bP^2)` = a - 2bP = c, значит P = (a-c)/2b и Q = a - (a-c)/2
А нужно делать именно так: MR = c = (P*Q)` = ((aQ - Q^2)/b)` = (a - 2Q)/b и уже отсюда искать Q.
Почему, по-моему, правильный первый пункт? Потому что MR это тоже цена, цена, которую получает продавец от реализации конкретной единицы продукции. Если мы идем по первому пути, то у нас цена равна цене, а по второму: цена равна количеству.
По второму вопросу: MR - это изменение выручки при росте количества на единицу, а не при росте цены на единицу - это разные вещи. MC - это изменение издержек при росте количества на единицу.
По поводу отдельного вопроса: то есть получается второй вариант правильный?