Пусть у нас имеется фрагмент некоторой функции спроса:
Рассмотрим формулу точечной эластичности:
$E_x^y=y'(x)\cdot(\dfrac{x}{y})$
В данной записи геометрический смысл первого сомножителя - тангенс угла наклона касательной, проведенной к функции в некоторой интересующей нас точке, второго - тангенс угла наклона луча, проведенного из начала координат к точке, в которой мы хотим вычислить точечную эластичность. Построим:
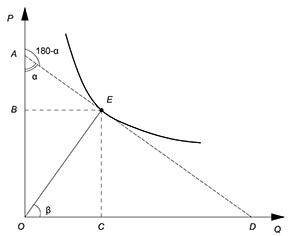
$E_x^y=y'(x)\cdot(\dfrac{x}{y})=-{tg\alpha}\cdot{tg\beta}$
$tg\alpha=\dfrac{BE}{AB}$
$tg\beta=\dfrac{CE}{CO}$
$E_x^y=-\dfrac{{BE}\cdot{CE}}{{AB}\cdot{CO}}$
$BE=CO$
$CE=BO$
$E_x^y=-\dfrac{BO}{AB}$
Также:
$E_x^y=-\dfrac{CD}{CO}$
Аналогично выводится геометрический смысл точечной эластичности предложения, а также любой другой функции (только необходимо следить за тем, какая переменная является зависимой, а какая независимой).
Возьмем функцию предложения:
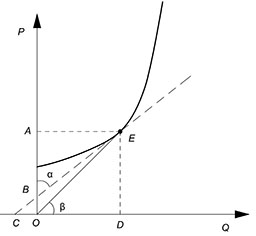
$E_x^y=y'(x)\cdot(\dfrac{x}{y})={tg\alpha}\cdot{tg\beta}$
$tg\alpha=\dfrac{AE}{AB}$
$tg\beta=\dfrac{DE}{DO}$
$E_x^y=\dfrac{{AE}\cdot{DE}}{{AB}\cdot{DO}}$
$AE=DO$
$DE=AO$
$E_x^y=\dfrac{AO}{AB}$
Также:
$E_x^y=\dfrac{CD}{DO}$
Геометрическим смыслом точечной эластичности удобно пользоваться, когда предложена линейная функция.
Пример 1
Дана функция предложения $Q=-10+P$, найти точечную эластичность при $Q=5$
Решим задачу, заодно найдем геометрический смысл точечной эластичности предложения.
$Q=5$, $P=15$
Изобразим нашу функцию, сделаем обозначения:
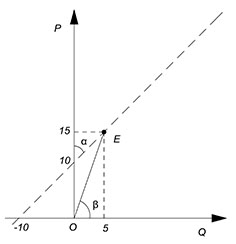
$E_x^y=\dfrac{AO}{AB}=\dfrac{15}{5}=3$
Геометрический смысл дуговой эластичности:
Рассмотрим случай с функцией спроса:
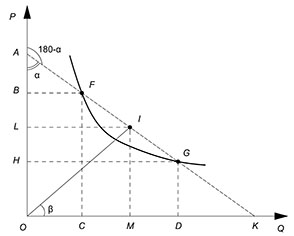
Вычислим дуговую эластичность в точке I.
Помним, что
$E^y_x={\dfrac{y_F-y_G}{x_F-x_G}}\cdot{\dfrac{(x_F+x_G)/2}{(y_F+y_G)/2}}$
Первый сомножитель - тангенс угла наклона хорды, проведенной через F и G к положительному направлению оси P. Геометрический смысл второго сомножителя - тангенс угла наклона луча, проведенного из начала координат к точке I (I - середина отрезка FG).
$E_x^y=-{tg\alpha}\cdot{tg\beta}$
$tg\alpha=\dfrac{IL}{AL}$
$tg\beta=\dfrac{IM}{MO}$
$E_x^y=-\dfrac{{IL}\cdot{AL}}{{IM}\cdot{MO}}$
$IL=MO$
$IM=OL$
$E_x^y=-\dfrac{LO}{AL}=-\dfrac{KM}{MO}$
Пример 2
Пусть имеется некоторая функция спроса. В точке F цена равна 20, а преобретаемое количество товара - 15. В точке G цена равняется 10, покупатели готовы купить по такой цене 30 единиц продукции. Найти дуговую эластичность при переходе из одной точки в другую, используя ее геометрический смысл.
Построим график, проведем хорду через точки F и G, обозначим точку I - середину данного отрезка, проведем луч, выходящий из начала координат к этой точке, сделаем обозначения на осях:
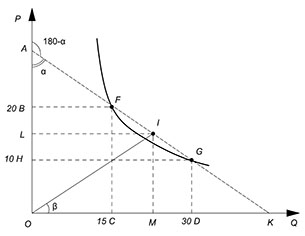
Как мы знаем:
$E_x^y=-\dfrac{LO}{AL}=-\dfrac{KM}{MO}$
Нам нужны координаты точек L и A. Чтобы узнать координату точки A, выведем функцию хорды:
$ \begin{cases}
30=10a+b
\\
15=20a+b
\\
\end{cases}
$
Получим $Q=45-1,5P$
Откуда координата точки A - $(45;0)$
Координаты точки L - как середины отрезка BH - $\dfrac{10+20}{2}=15$ $(15;0)$.
$E_x^y=-\dfrac{LO}{AL}=-\dfrac{15}{15}=-1$



 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ