1.3 Производная

Некоторые функции могут не иметь производной во всех или в некоторых точках (если, например изменения функции являются резкими, а не гладкими, функция терпит разрыв).

Здесь мы будем говорить о функциях, имеющих производную на всей области определения, гладких, без разрывов и изломов.

Возьмем некоторую непрерывную функцию $f(x)$, определенную на промежутке $(-\infty;\infty)$. 

Как мы видим, данная функция возрастает на промежутке $(-\infty;a)$;$(b;\infty)$, убывает на отрезке $(a;b)$, имеет 2 точки экстремума (в точке $a$ - максимум, в точке $b$ - минимум). 

Очевидно, что на промежутке $(-\infty;a)$ функция $f(x)$ является более пологой, чем на промежутке $(b;\infty)$. На первом промежутке скорость её возрастания является меньшей, чем на втором.

Обратимся к графику функции. 

Зафиксируем произвольные точки $x_0$ и $x_1$ на возрастающих участках нашего графика. Сейчас мы находимся в точках с координатами $(x_0;y(x_0))$ и $(x_1;y(x_1))$. Совершим переход в новые точки, лежащие на графике функции $f(x)$. Пусть прирост аргумента функции для обоих случаев будет равен некоторому числу $\Delta x$ , одинаковому для обоих случаев. Координаты новых рассматриваемых нами точек будут равны соответственно $(x_{0}+\Delta x; y(x_{0}+\Delta x))$ и $(x_{1}+\Delta x; y(x_{1}+\Delta x)$. В обоих случаях прирост нашего аргумента был одинаковым, но приросты функции
($\Delta y_0 = y(x_0+\Delta x)-y(x_0)$ и $\Delta y_1 = y(x_1+\Delta x)-y(x_1)$) оказались различны $(\Delta y_0 \neq \Delta y_1)$. Это произошло, потому что скорость возрастания функции на рассматриваемых участках $(-\infty;a)$ и $(b;\infty)$ различна. Прирост функции на втором участке оказался больше, чем на первом, потому что функция на втором участке возрастает круче, скорость её возрастания на втором участке больше. 

Измеряем скорость возрастания функции на первом участке: $v_0=\dfrac{\Delta y_0}{\Delta x}$ и на втором: $v_1=\dfrac{\Delta y_1}{\Delta x}$. Очевидно, что $v_0 < v_1$. 

(Обратим внимание на отрезок, соединяющий точки $A_0$ и $B_0$, $A_1$ и $B_1$. Данный отрезок называется секущей. Он является гипотенузой в прямоугольном треугольнике $A_0B_0C_0$. Рассмотрим данный треугольник: $tg \alpha=\dfrac{B_0C_0}{A_0C_0}=\dfrac{\Delta y}{\Delta x}$. Запомним эту информацию, она нам пригодится при определении геометрического смысла производной.)

В рассмотренном выше случае при измерении скорости изменения (в нашем случае возрастания) функции мы взяли довольно большие отрезки приращения аргумента, поэтому наши представления о том, что происходит с функцией $f(x)$ на выбранных промежутках являются довольно туманными (мы знаем только, что функция на обоих промежутках  возрастает и что скорость её возрастания больше на втором промежутке). 

А что будет, если взять бесконечно малый отрезок  $\Delta x$?  Пусть $\Delta x$ стремится к $0$ (принимает бесконечно малые значения, близкие к $0$, тем не менее никогда его не достигая). Тогда мы сможем посчитать прирост функции $\Delta y$ на очень малых промежутках в окрестности выбранной нами точки, фактически узнать скорость роста функции в данной точке. Это и будет производной функции в данной точке. 

Определение 1
Производной функции в точке $x_0$ называется предел отношения приращения $\Delta y$ функции в точке $x_0$  к приращению $\Delta x$ аргумента, когда последнее стремится к $0$. 

$\lim\limits_{\Delta x\to 0} \dfrac {\Delta y}{\Delta x}=\lim\limits_{\Delta x\to 0}\dfrac {y(x_0+\Delta x)-y(x_0)}{\Delta x}=f’(x_0)$

В данной формуле $lim$ - предел - показывает, к какому числу стремится (то есть бесконечно приближается, но не достигает) выражение, находящееся под знаком предела, при приросте аргумента, стремящемся к $0$. 

Геометрический смысл производной

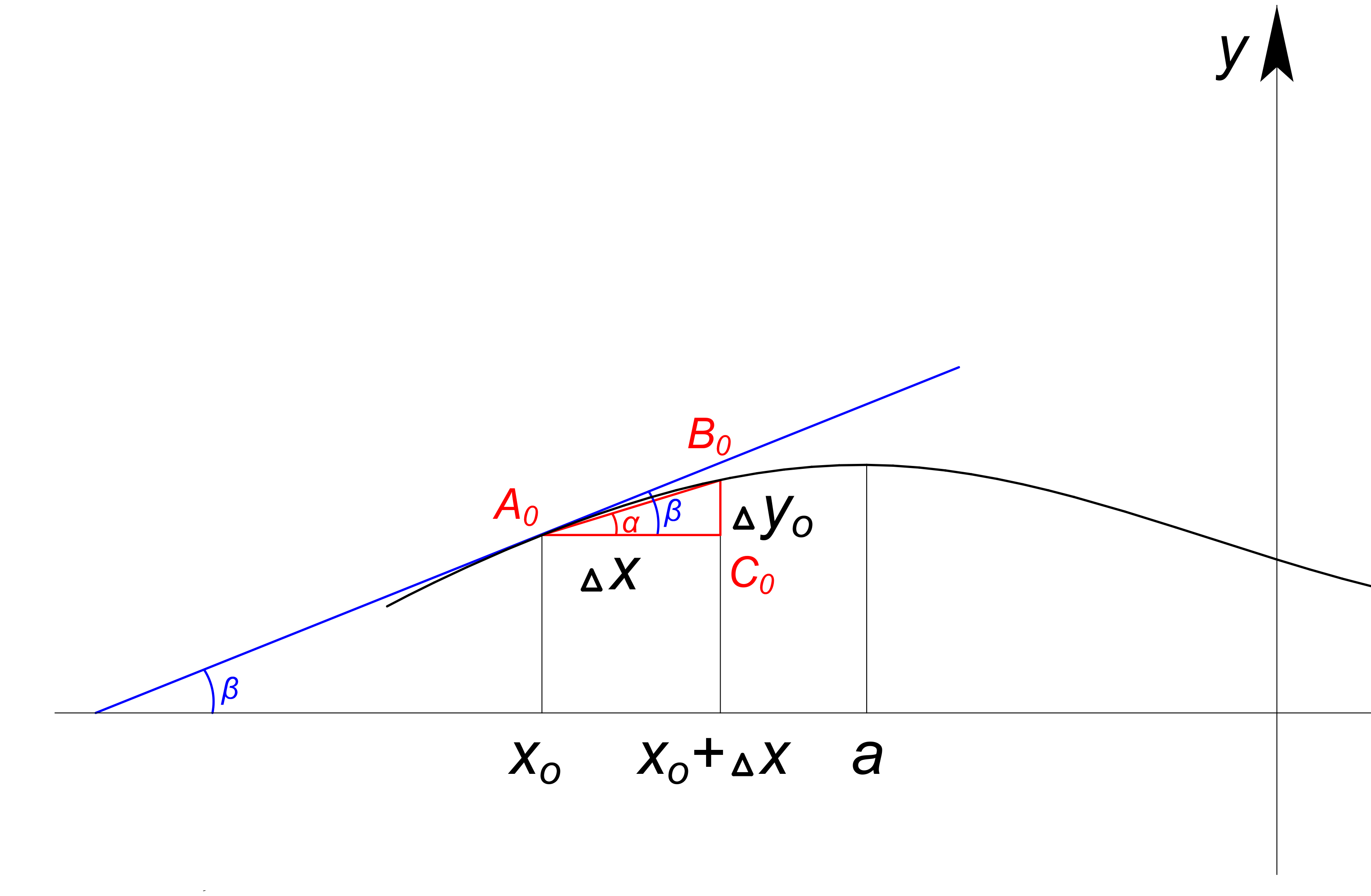
Вновь обратимся к графику нашей функции. $A_0B_0$ является при выбранном нами $\Delta x$, как мы помним, секущей. Будем постепенно уменьшать отрезок $\Delta x$. Вместе с этим будет уменьшаться и приращение нашей функции $\Delta y$, точка $C_0$ будет бесконечно близко приближаться к точке $A_0$  по горизонтали, точка $B_0$ будет также приближаться к точке $A_0$, но уже вдоль функции $f(x)$. Таким образом, секущая будет стремиться знать место касательной, проведенной к графику функции. Получается, что $tg \alpha = \dfrac{\Delta y}{\Delta x}$ становится $\lim\limits_{x\to 0} \dfrac {\Delta y}{\Delta x}=f’(x_0)= tg \beta $.

$tg\beta$ - тангенс угла наклона касательной, проведенной к точке $x_0$;

Уравнение касательной в точке $x_0$ имеет вид: $y=f(x_0)+f'(x_0)(x-x_0)$, где $f(x_0)$ является значением функции в данной точке $x_0$, $f'(x_0)$- значением производной функции $f(x)$ в точке $x_0$ , $x$ - переменная.

Производная как функция
До этого момента мы рассматривали производную в конкретной точке функции $f(x)$, но ведь для нахождения производной (дифференцирования) можно взять любую точку функции $f(x)$. Заменим в наших формулах $x_0$ на переменную $x$, получим:

$\lim\limits_{\Delta x\to 0} \dfrac {\Delta y}{\Delta x}=f’(x)$;

$\lim\limits_{\Delta x\to0} \dfrac {\Delta y}{\Delta x}=\lim\limits_{x\to 0} \dfrac {y(x+\Delta x)-y(x)}{\Delta x}=f’(x)$;

Теперь у нас имеется другая функция ($y=f’(x)$), характеризующая скорость изменения нашей исходной функции $f(x)$.

Если функция $f(x)$ возрастает на каком-либо промежутке, её прирост больше $0$, то её производная на данном промежутке положительна.

Если функция $f(x)$ принимает наибольшее или наименьшее значение в какой-либо точке (при этом она является непрерывной в этой точке), обладает в этой точке горизонтальной касательной, то её производная в данной точке обращается в $0$.

Если функция $f(x)$ убывает на каком-либо промежутке, её прирост меньше $0$, то её производная на данном промежутке отрицательна.

Пользуясь данным свойством производных, можно искать точки экстремума функции. Для этого необходимо взять производную $f’(x)$  функции $f(x)$, приравнять её к $0$, найти промежутки, на которых производная отрицательна и на которых она положительна. Точка, где производная равна $0$, а её знак меняется с $-$  на  $+$, будет точкой минимума функции  $f(x)$ (сначала она убывала, потом достигла наименьшего значения, потом начала возрастать). Точка, где производная равна $0$, а её знак меняется с $+$  на  $-$, будет точкой максимума функции  $f(x)$ (сначала она возрастала, потом достигла наибольшего значения, потом начала убывать).  

Алгоритм нахождения максимума/минимума функции:

1. Находим область определения функции;
2. Находим производную функции на области определения;
3. Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (все перечисленные точки называются точками возможного экстремума, проходя через эти точки производная может изменять свой знак, а может и сохранять (если в числителе или знаменателе, например, имеются множители в четной степени, производная свой знак не меняет);
4. Выбираем точки, в которых функция непрерывна, и проходя через которые, производная меняет знак - они и являются точками экстремума.

Также проверить, является ли данная точка максимумом или минимумом функции можно, используя вторую производную ($f’’(x)$), функции  $f(x)$, которая является в свою очередь производной функции $f’(x)$.

Если $f’’(x)>0$, то данная точка является точкой минимума;
Если $f’’(x)<0$, то данная точка является точкой максимума;
Если $f"(x)=0$, исходная функция имеет в этом месте точку перегиба;

Обратимся к графикам:

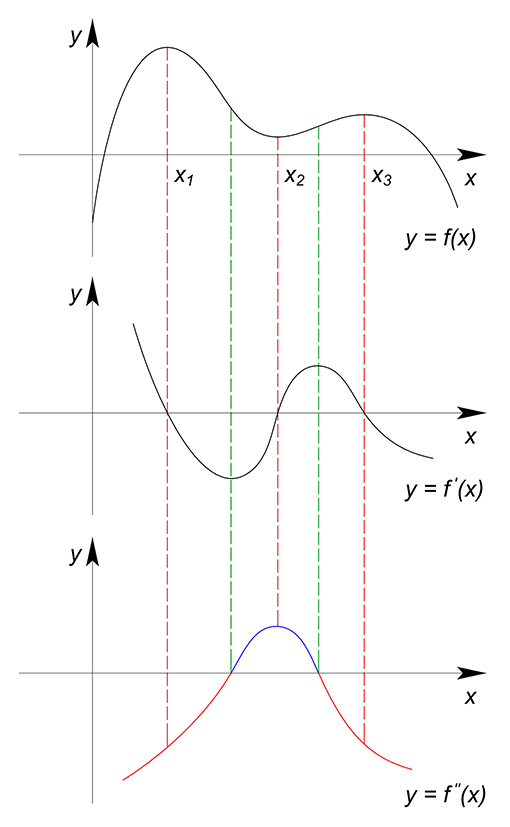
На данной картинке изображены (сверху вниз):

1. график функции $f(x)$;
2. график функции $f'(x)$;
3. график функции $f''(x)$;

В точках, где функция $f(x)$ достигает своего наибольшего/наименьшего значения, производная функции $f'(x)$ равна $0$. В точках перегиба функции $f(x)$ её производная достигает максимума/минимума. Вторая производная $f''(x)$ больше нуля на промежутке возрастания функции $f'(x)$, меньше нуля на промежутках её убывания. Обратим внимание на точки $x_1$, $x_2$, $x_3$, являющиеся точками экстремума функции $f(x)$. Точкам минимума функции $f(x)$ соответствуют участки, где $f''(x)$ меньше нуля, точки максимума - где больше.

 Таблица производных некоторых функций:

 

Функция	Производная
$k$ (постоянная)	$0$
$kx+b$	$k$
$x^a$ ($a \in R$,)	$ax^{a-1}$

P.S. $\sqrt x = x^{\frac{1}{2}}$
$\dfrac{1}{x}=x^{-1}$ - верно не только для степени $-1$

Правила дифференцирования

$(cv)’=cv’$, где $c$ является константой;

$(v+u)’=v’+u’$;

$(v-u)’=v’-u’$;

$(vu)’=v’u+vu’$;

$\left(\dfrac{v}{u}\right)’=\dfrac{v’u-u’v}{u^2}$;

Пример 1

Найти производную функции $f(x)=ax^2+bx+c$

$f’(x)=2ax+b$;

Дифференцирование сложной функции

(Сложная функция – функция от функции; если у нас есть функции $f(x)$, $y(f)$, то функция $y(f(x))$ будет сложной)

Чтобы взять производную от сложной функции, необходимо прежде взять производную от внешней функции, потом домножить её на производную от внутренней функции. 

Пример 2

Найти производную функции $f(x)=\sqrt{5x+1}$

$f(x)=(5x+1)^{\frac{1}{2}}$;

$f’(x)=\times{\dfrac{1}{2}}{(5x+1)^{\frac{1}{2}-1}}{5}=\dfrac{5}{2\sqrt{5x+1}}$;

Пример 3 - оптимизация функции

 Найти наибольшее и наименьшее значение функции $f(x)=x^2-4x+4$ на промежутке $[0;5]$

По формуле вершины параболы точку вершины параболы можно найти следующим образом:

$x^*=\dfrac{-b}{2a}=\dfrac{4}{2}=2$

$a>0$, следовательно, данная функция является параболой с ветвями вверх, точка экстремума будет точкой минимума.

Теперь воспользуемся производной:

$f’(x)=2x-4=0$;

$2x=4$;

$x=2$;

На промежутке $(-\infty;2)$ производная $f’(x)$ меньше $0$,  следовательно, $f(x)$ убывает;
на промежутке $(2;\infty)$ производная $f’(x)$ больше $0$,  следовательно, $f(x)$ возрастает. В точке $2$ $f’(x)=0$,  следовательно, данная точка есть точка экстремума - минимума.

$y(2)=0$;

Или: $f’’(x)=2>0$, следовательно данная точка является точкой минимума.

Точка условного максимума будет на концах данного отрезка:

$f(0)=4$;

$f(5)=9$;

Наибольшее значение функции на данном отрезке равно $9$, наименьшее - $0$.