6.3 Функция спроса на совершенно конкурентном рынке труда

Так как фирма работает на совершенно конкурентном рынке труда, то она воспринимает ставку заработной платы, сложившуюся на рынке, как заданную, $w=const$. Функция предложения труда для одной фирмы представляет собой прямую линию, параллельную оси абсцисс, проходящую на уровне равновесной рыночной ставки заработной платы, $w^*=MC_L$.

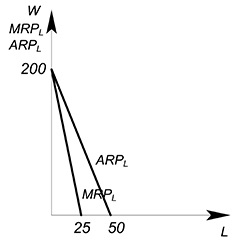
Фирма выбирает оптимальный для себя объем труда, исходя из стремления максимизировать прибыль. Кривой спроса фирмы на труд является нисходящая ветвь $MRP_L$ (не работаем на восходящем участке, ибо там максимум убытков) ниже наибольшего значения $ARP_L$ (в $SR$ фирма работает, если $TR\ge VC$, поедим обе части уравнения на $L$, получим $ARP_L\ge w$)

Пример
Некоторая фирма является монополистом на рынке товара. Функция спроса на ее товар имеет вид $Q=100-P$. Технология изготовления данного товара описывается функцией $Q=2L$. Вывести функцию спроса фирмы на труд.

$P(Q)=100-Q$

$\pi(Q)=100Q-Q^2-TC(Q)$

$TC(Q)=VC(Q)+FC$

Так $w=const$, ибо рынок труда совершенно конкурентный, то $VC=w\cdot L$

Таким образом, получаем:

$\pi(L)=200L-4L^2-wL-FC$

Фирма максимизирует прибыль, при каждом возможном уровне ставки заработной платы она будет нанимать оптимальное число рабочих, соответствующих условию максимизации прибыли:

$\pi'(L)=200-8L-w=0$

$\pi''(L)=-8<0$, следовательно, максимум.

Делаем еще одну проверку (уходит ли фирма или остается):

$TR(L)=200L-4L^2$

$ARP_L=200-4L$, всегда выше функции $w=200-8L$

Получаем функцию спроса фирмы на труд:

$L=25-0{,}125w$

$Max \pi$ в зависимости от рынка товара и ресурса:

Общие условия: $MR(L)\cdot MP_L = w'(L) + w (L)$ (берем производную сложной функции: $VC(L)=w(L)\cdot L$, $VC'(L)=w'(L) + w(L)$ -по правилу дифференцирования суммы. Аналогично поступаем с $TR$.

1. Если товарный рынок совершенно конкурентный, рынок труда нет, то $P\cdot MP_L = w'(L) + w(L)$
2. Если ресурсный рынок совершенно конкурентный, то $MR \ cdot MP_L=w$
3. Если оба рынка совершенно конкурентные, то $P\cdot MP_L =w$

Всегда не забываем делать проверку, остается ли фирма на рынке! ($MRP_L \le ARP_L$)