Спрос на рынке крокодилов описывается функцией $P=24-5Q$.
Государству не нравится то, монополист не продает часть произведенных крокодилов, и оно решило ввести обязательную утилизацию нераспроданного товара. Монополист теперь обязан утилизировать нераспроданных крокодилов, причем издержки этого процесса составляют $C_{util}=(Q_{produced}-Q_{sold})^2$.
1. Какая будет получена прибыль до введения обязательной утилизации?
2. Предположим, требование об обязательной утилизации вступило в силу. Найдите функцию издержек монополиста в общем случае ($TC(Q_{sold})$) и постройте график этой функции. Верно ли, что $TC(Q_{sold})$ возрастает?
3. Какую сумму фирма готова заплатить за отмену требования об обязательной утилизации?
4. Какому известному утверждению противоречит поведение монополиста в данной задаче?
P.S. Гриша, спасибо за замечательный пример товара!)

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ
Комментарии
2)
а можно так?
$TC=\left\{\begin{matrix} 0, Qsold=0& \\ \frac {max[Qsold,1]}{4}+(max[Qsold,1]-Qsold)^2, Qsold\leq 1 & \\ \frac {max[Qsold,2]}{4}+(max[Qsold,2]-Qsold)^2,1< Qsold\leq 2& \\ \frac {max[Qsold,3]}{4}+(max[Qsold,3]-Qsold)^2,2
Дани-ил!
Update. Насчет того "как убрать amp" попробуй написать так :
$$TC(Q_{sold}) =\begin{cases}0,\text{если $Q_{sold}=0$} \\ \frac{max[ Q_{sold};1]}{4}+(max[ Q_{sold};1]-Q_{sold})^2 \\\frac{max[ Q_{sold};2]}{4}+(max[ Q_{sold};2]-Q_{sold})^2\\\frac{max[ Q_{sold};3]}{4}+(max[ Q_{sold};3]-Q_{sold})^2 \end{cases}$$
Араик, неверно, там именно $28.05$, какое у тебя $Q_{sold}$ получается?
2. Гор, верно, но там можно проще записать, вообще без функции $max[]$. И под "общим случаем" я имел в виду записать функцию в виде
$$TC(Q_{sold})=\begin{cases}0,\text{ если $Q_{sold}=0$} \\f(Q_{sold},a),\text{если $a-1
На счет 2-го: Это функция издержек, которую вроде Гор написал, просто я сделал так, чтобы $amp;$ не появлялось))
На счет 3-го: Я и не писал, что продам $2.375$)) Я считал, что продам $2$)) Видимо это неверно)
Рекомендую сначала нарисовать график издержек для первого случая и выписать функцию издержек
В оптимуме $Q_{produced}$ и правда $3$, но вот $Q_{sold}$ неверное!
Рассказывай, как искал)'
И на всякий случай напиши функцию издержек (для пункта 1)
Мы произведем Q=3, TC=3/4
Теперь думаем, сколько нужно продать, чтобы получить, как можно больше, при фиксированном TC. То есть максимизируем выручку, TR max при Q=2,4. Тогда прибыль ровно 28,05
А теперь подумай о этой точке, где она находится.
Может такое быть и при субсидии, например, что тоже не совсем искусственный пример.
т.е. $max[3,5]=5$
А по поводу функции издержек может так?
$$TC(Q_{sold}) =\begin{cases} \frac{[Q_{sold}]+1}{4}+([Q_{sold}]+1-Q_{sold})^2, $Q_{sold}\notin\mathbb{Z}$;} \\ $\frac{Q_{sold}}{4}$,$Q\in\mathbb{Z}$ \end{cases}$$ →
Где $[Q_{sold}]$ - целая часть от числа $Q_{sold}$
Ведь если бы диапазон целых Q был бы например больше 10, то такую систему как у Гора не записать было бы :)
Но твоя версия мне больше нравится
попробуй записать для промежутка $a-1
1) $$TC(Q_{sold}) =\begin{cases}\frac{1}{4},\text{если $Q_{sold} \in (0;1]$} \\ \frac{2}{4} ,\text{если $Q_{sold} \in (1;2]$} \\\frac{3}{4} ,\text{если $Q_{sold} \in (2;3]$}\\\frac{4}{4} ,\text{если $Q_{sold} \in (3;4]$} \end{cases}$$ Записываем функцию прибыли для каждого промежутка (если $\pi_{i}=Q_{sold}(24-5Q_{sold})-TC_{i})$, где $TC_{i}$ - издержки для каждого промежутка, с учетом ограничений по $Q$) Получаем максимальную прибыль $28.05$
2) Новые $TC(Q{sold}):$ $$TC(Q_{sold}) =\begin{cases}\frac{1}{4}+(1-Q_{sold})^2,\text{если $Q_{sold} \in (0;1]$} \\ \frac{2}{4}+(2-Q_{sold})^2 ,\text{если $Q_{sold} \in (1;2]$} \\\frac{3}{4}+(3-Q_{sold})^2 ,\text{если $Q_{sold} \in (2;3]$}\\\frac{4}{4}+(4-Q_{sold})^2 ,\text{если $Q_{sold} \in (3;4]$} \end{cases}$$
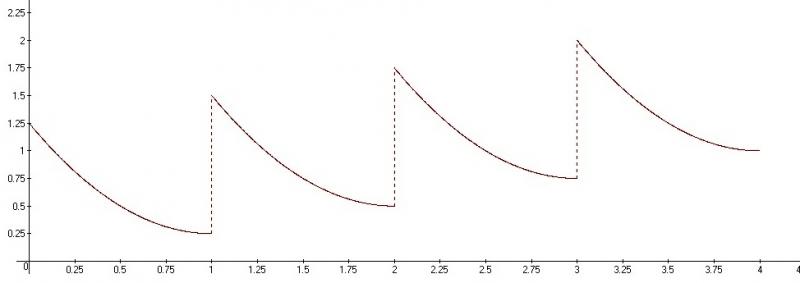
Дальше записываем функцию прибыли как здесь для каждого участка, "выигрывает" 3-ий участок, там $\pi=27.75, Q^{*}_{sold}=2.5$
3) Соответственно ответ на вопрос $28.05-27.75=0.3$
4) Я уже писал выше))
P.S. Для интересующихся: Какие точки на графике надо выколоть и надо ли вообще? (Вопрос от автора, вроде(:))
PS Красаучик Араик, столько оформлял небось :D
Кстати все это оформлялось постепенно, в течении двух дней )) Мне самому было интересно, как выглядят издержки, а предельные издержки выглядят еще лучше)