В олимпиадах
Баллы
Свойства
Сложность
13.01.2017, 05:49
(0)
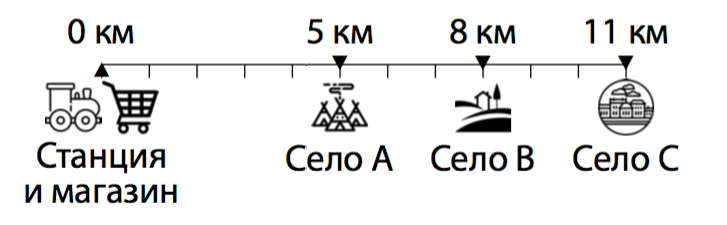
От станции до последнего села часто ходит маршрутка, проезд в которой стоит 1 рубль за километр. Маршрутка может останавливаться в любом месте для посадки и высадки пассажиров.
Каждый житель сёл любит свежий хлеб (и не ест вчерашний) и съедает в день 1 буханку хлеба. Когда выпускник РЭШ Федор оказался в этих местах, он узнал, что каждый житель ездит сам за хлебом на маршрутке до станции, где тот продается по 15 рублей за буханку. Федор решил помочь жителям сёл с доставкой хлеба.
Хитрый выпускник РЭШ нашел небольшой фургончик и решил доставлять хлеб в точку $S$, расположенную на проселочной дороге. Оценив спрос, каждое утро он будет закупать хлеб в магазине на станции, везти его до точки $S$, там продавать всем желающим, а вечером везти пустой фургон обратно на станцию. Расходы на бензин составляют 0,5 рубля за километр пути.
Считайте, что жители сёл принимают решение о покупке хлеба исключительно на основании минимизации расходов (цена хлеба плюс расходы на проезд на маршрутке), а при равенстве расходов предпочитают покупать хлеб у Фёдора, а не в магазине.
В какой точке дороги Федору нужно поставить фургон и по какой цене продавать хлеб, если он хочет получить максимальную прибыль (разницу между выручкой от продажи и затратами на закупку хлеба и на бензин)?
Иллюстрации к задаче 3 созданы Freepik.
Все задачи этой олимпиады
| Задача | Баллы |
|---|---|
| 1. Спрос и цены | 7 |
| 2. Авиаперелеты из Москвы | 5 |
| 3. Торговля свежим хлебом | 12 |
| 4. Дефицит врачей | 7 |
| 5. Расчет издержек | 10 |
| 6. Онлайн-аукционы рекламы | 20 |
| 7. Ярмарка картошки |

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ