2.1 Кривая производственных возможностей

Как известно, главной проблемой экономики является удовлетворение (а точнее его невозможность) безграничных человеческих потребностей в условиях ограниченности располагаемых ресурсов. Ограниченное количество имеющихся у нас ресурсов позволяет произвести конечное количество благ и услуг.

Определение 1
Кривая производственных возможностей, о которой пойдет речь в данной теме, показывает все возможные комбинации производства различных благ при условии полного и эффективного использования имеющихся ограниченных ресурсов.

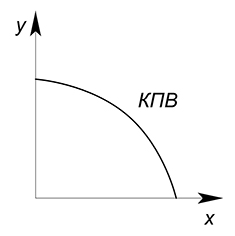Предпосылки построения КПВ:

1. В экономике производятся только два вида товаров/услуг;
2. В экономике должна применятся самая эффективная технология из всех существующих на данный момент.

Обратимся к графику некоторой КПВ:

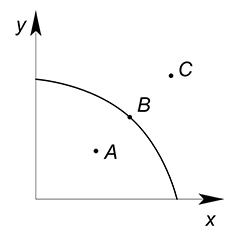
Область, ограниченная графиком КПВ, показывает все доступные нам точки при данном запасе ресурсов и данной технологии.

Рассмотрим $3$ точки:

Точка $A$ лежит под графиком КПВ. Данная точка является неэффективной по Парето (был такой итальянский учёный), потому что можно увеличить объём производства одного блага, не уменьшая количество другого.

Точка $B$ является эффективной по Парето, ибо нельзя увеличить объём производства одного блага, не уменьшая объём производства другого блага.

Точка $C$ является недостижимой при имеющемся количестве ресурсов и данной технологии.

В неэффективную точку можно попасть, если ресурсы используются неэффективно

Функция КПВ

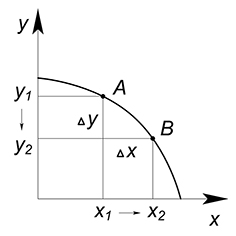
КПВ - невозрастающая функция.
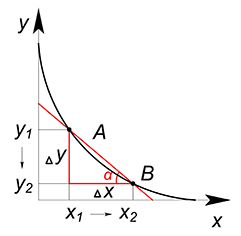
В большинстве случаев КПВ является убывающей функцией. Возьмем произвольную точку $A$, лежащую на графике функции КПВ. В данной точке уже задействованы в производстве товаров $x$ и $y$ все имеющиеся ресурсы. Чтобы увеличить производство товара $x$ ($x_1 \to x_2$), нам придётся уменьшить количество производимого товара $y$ ($y_1 \to y_2$) (уменьшая объём производства товара $y$, мы освобождаем некоторое количество ресурсов, которые теперь пойдут на производство дополнительных единиц товара $x$). Таким образом, мы имеет положительный прирост аргумента $(x_2-x_1 > 0)$ и отрицательный прирост значения функции $(y_2-y_1<0)$. Большему значению аргумента соответствует меньшее значение функции, следовательно, данная функция является убывающей.

Альтернативная стоимость и КПВ

Определение 2
Альтернативная стоимость показывает от какого количества единиц другого блага (например, блага $y$) нужно отказаться для производства одной дополнительной единицы первого блага (например, блага $x$)

Геометрический смысл альтернативной стоимости

Наиболее часто встречающимися графиками КПВ являются линейная и вогнутая функции.

Разберем геометрический смысл $AC$ на примере вогнутой функции:

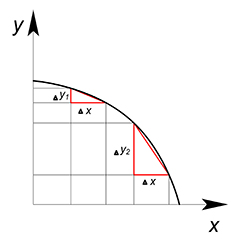
Если мы работаем с дискретными величинами, прирост $x$ и прирост $y$ являются целыми числами, альтернативная стоимость дополнительной единицы $x$ равна $\dfrac{\Delta y}{\Delta x}=tg\alpha$, то есть тангенсу угла наклона секущей. (Деля $\Delta y$ на $\Delta x$ мы ищем сколько единиц товара $y$ приходится на дополнительную единицу товара $x$).

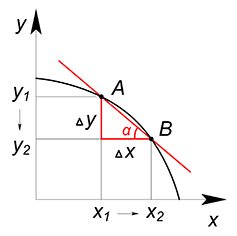
Но во многих экономических задачах товары считаются бесконечно делимыми. В таком случае нам нужно посчитать то количество товара $y$ от которого нам пришлось отказаться, чтобы произвести дополнительное бесконечно малое количество товара $x$. В данной ситуации альтернативная стоимость товара $x$ в некоторой точке $A$ (АС приращения $x_A$ на бесконечно малую величину) - это угол наклона касательной в этой точке, то есть производная функции КПВ.

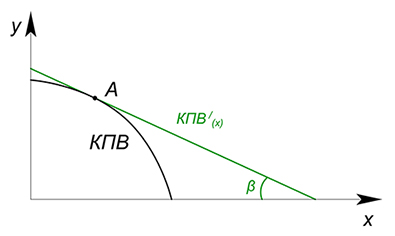
Подробнее о производных и секущих вы можете узнать здесь.

Закон, актуальный для вогнутых функций:
При увеличении объёмов производства товара его альтернативная стоимость растет ($\Delta y_2>\Delta y_1$). Товар может обладать возрастающей альтернативной стоимостью, ибо при увеличении количества одного товара для его производства используются всё менее и менее приспособленные ресурсы. Вогнутость КПВ обусловлена невзаимозаменяемостью ресурсов.

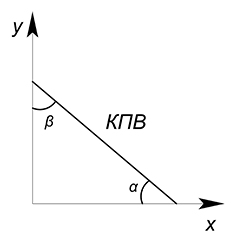
Линейная функция обладает постоянной альтернативной стоимостью на всём своём протяжении. Её альтернативная стоимость вычисляется также как и у вогнутой функции (только работаем мы теперь не с касательной и секущей, а с графиком самой функции). Товар может обладать постоянной альтернативной стоимостью, если ресурсы, необходимые для его производства являются более или менее взаимозаменяемыми.

$AC_x=tg\alpha$
$AC_y=tg\beta$

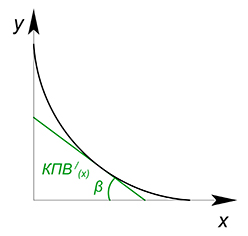
Также нельзя забывать про существование выпуклых функций КПВ. Подобные КПВ обладают убывающей альтернативной стоимостью из-за возрастающей отдачи от масштаба: если мы задействуем в производстве товара много ресурсов, то получается производить его с меньшими издержками. $AC$ данных функций измеряется также, как и любых других, и равна тангенсу угла наклона касательной, проведенной в точку касания при бесконечно делимом $x$ ($AC_x=tg\beta$) или тангенсу угла наклона секущей ($AC_x=tg\alpha$) при работе с дискретными величинами.

Ещё существуют КПВ с разной выпуклостью на разных участках.