В результате вооружённого переворота в стране Тригоноляндии к власти пришёл король Филипп I. Сосредоточив в своих руках все инструменты фискальной и монетарной политики, Филипп решил как можно быстрее определиться с целевыми показателями инфляции и безработицы, чтобы начать действовать.
«Из всех доступных комбинаций инфляции и безработицы я выберу ту, что будет максимизировать полезность общества во благо всеобщего процветания!» – произнёс Филипп во время коронации.
Помятуя о существовании кривой Филлипса, показывающей взаимосвязь между инфляцией и безработицей в краткосрочном периоде, монарх поручил компании Philips Electronics в рамках проекта «Изменим жизнь к лучшему!» описать множество комбинаций инфляция – безработица, из которого он мог бы выбрать оптимальную. Почти завершив исследование, главный аналитик компании Philips Electronics исчез при загадочных обстоятельствах. В его кабинете был найден листок бумаги с двумя формулами:
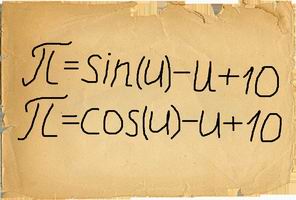
Подходили сроки окончания проекта, и нужно было сообщить королю множество доступных комбинаций. В компании Philips Electronics догадались, что формулы на листке – кривые Филлипса (π – темп инфляции в процентах, u – уровень безработицы в процентах), но не знали, какую из двух формул выбрать. Опасаясь совершить роковую ошибку и помня о том, что «истина всегда лежит между крайностями», директор компании Philips Electronics сообщил королю следующее: «Вы можете выбрать любую точку на плоскости инфляция – безработица, лежащую между этими двумя кривыми». Король не заставил себя долго ждать: «Максимизирует общественную полезность точка A», – вымолвил он, нарисовав две кривых и указав монаршим перстом на одну из точек между ними.
С тех пор экономика Тригоноляндии находилась в точке A. Но в один прекрасный день в канцелярию Его Величества пришло письмо от Филиппинского экономического общества, в котором говорилось, что кривые Филлипса устарели, а множество доступных комбинаций инфляции и безработицы теперь описывается с помощью индекса Филлипса
$I_{Ph} (\pi ,u) = (\sin (u) - u + 10 - \pi )*(\pi - \cos (u) + u - 10)$,
а именно: можно выбирать любое сочетание π и u, лишь бы $I_{Ph} $ был неотрицательным. Также в письме говорилось о том, что, учитывая новое множество доступных комбинаций, общественная полезность Тригоноляндии теперь максимизируется не в точке A, а в точке B (к письму прилагался рисунок с указанием этой точки).
Король Филипп I проанализировал новое множество доступных комбинаций и сделал вывод, что если это множество описано верно, то рекомендация по переходу из точки A в точку B ошибочна.
Докажите правильность этого вывода.
Факультет экономических наук НИУ ВШЭ
Комментарии
1 Определим где вообще в первом случае мог быть оптимум, заметим что имея две кривых $\pi=\sin(u)-u+10$ и $\pi=\cos(u)-u+10$ для выбора оптимума мы всегда будем брать точку на той части одной кривой, которая лежит соответственно под частью второй кривой, тогда все возможные точки оптимума будут лежать на кривой обведенной зеленым цветом.
2 Из полученного идекса Филлипса выразым $\pi$, то есть решим относительно него квадратное уравнение с параметром. Получим $\pi_1=\frac{-\sin(u)-\cos(u)+2u-20+\sqrt{(\sin(u)-\cos(u))^2-4I_p_h}}{2}$ или $\pi_2=\frac{-\sin(u)-\cos(u)+2u-20-\sqrt{(\sin(u)-\cos(u))^2-4I_p_h}}{2}$
Pассмотрим оба варианта
2.1.
Очевидно чем меньше значение $\pi_1$ при каждом $u$ тем выгоднее нам, тогда свое мин значение $\pi_1$ принимает в точке где $I=0$, далее кривая отражает уже менее выгодные значения , то есть графически лежит правее и ниже . Заметим что при $I=0$ , $\pi_1=\frac{-\sin(x)-\cos(x)+2x-20+|\sin(x)-\cos(x)|}{2}$
Если подумать, то можно заметить, что это - ни что иное как зеленый график, симметрично отраженный отностительно оси $u$(это видно не только из графиков но и математически нетрудно обоснуемо), таким образом они имеют одну общуюю точку,принадлежащую оси $u$.Если же $I$ становится больше нуля, то на множестве полoжительных $u;\pi$ общих точек у них нет, тогда любая точка на зеленой кривой отражает более выгодное сочетание безработицы и инфляции чем $\pi_1$, где $I>0$.
2.2
График $\pi_1$ при увеличении $I$ наоборот сдвигается влево-вверх,однако ось $u$ он в любом случае пересечет правее чем это сделает $\pi_1$,следовательно,учитывая,что $\pi_2$ возрастающая ф-ция - общих точек у зеленой кривой и гр-кa $\pi_1$ на множестве полoжительных $u;\pi$ нет, следовательно любая точка на зеленой кривой предпочтительнее любой точки на $\pi_1$
$\pi_2(I_p_h=0)$ - голубой
Соображения о том, что чем меньше инфляция и безработица, тем лучше - разумные, но это не есть универсальная истина. Например, когда государство проводит стимулирующую политику и хочет снизить реальную процентную ставку, то низкая инфляция мешает: если инфляция 5%, то можно снизить реальную процентную ставка до -5%, а если инфляция 0%, то реальную ставку не удастся установить ниже нуля (всё это оттого, что номинальная ставка не может быть отрицательной - подумайте, почему).
Похожий аргумент: когда спрос на продукцию фирмы упал, и теперь ей оптимально установить меньшую реальную зарплату сотрудникам, то проще сделать это при положительной инфляции: тогда всего лишь придётся поднять зарплату меньше, чем в $1+\pi$ раз. Как ни удивительно, но люди реагируют на это гораздо спокойнее, чем на небольшое уменьшение номинальной зарплаты при нулевой инфляции. Такая иррациональная черта: обращать внимание на номинальные, а не на реальные показатели. Интересную статью на эту и похожие темы (на английском, правда) можно почитать здесь.
В любом случае, на решении данной задачи всё это никак не сказывается. В связи с этим совет Тимуру и всем: пробуйте сначала решить задачу в общем виде, и лишь при необходимости используйте дополнительные факты из условия. В данном случае, стоило задать такой вопрос: "а что, если инфляцию и безработицу заменить на две абстрактных переменных". Это позволяет концентрироваться на главном.
Из полученного идекса Филлипса выразым $\pi$, то есть решим относительно него квадратное уравнение с параметром. Получим,если вернуть минус на место
$\pi_1=\frac{\sin(u)+\cos(u)-2u+20+\sqrt{(\sin(u)-\cos(u))^2-4I_p_h}}{2}$ или $\pi_2=\frac{\sin(u)+\cos(u)-2u+20-\sqrt{(\sin(u)-\cos(u))^2-4I_p_h}}{2}$
Заметим, что при $I=0$ два данных графика образуют то же самое , что и изначальные два, при увеличении $I$, $\pi_1$ и $\pi_2$ "заполняют" собой множество, которое предложили королю для рассмотрения.
Таким образом при условии неотрицательности $I$, множетсво решений параметрического равенства совпадает с множеством представленным королю.Поэтому в первом и втором случае точки оптимума должны совпадать.