Рыночное предложение труда выглядит так:
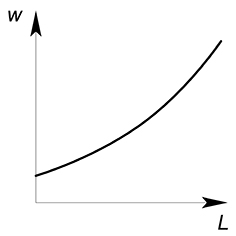
При увеличении величины ставки заработной платы количество работников, готовых трудиться, увеличивается.
Фирмы же предъявляют спрос на труд ($L_D$). Основной целью рационально действующй фирмы является максимизация прибыли. Прибыль фирмы зависит от объема произведенной продукции ($\pi(Q)$), который в свою очередь зависит от количества используемого для его изготовления фактора производства, в данном случае труда ($Q(L)$). Таким образом, функция прибыли фирмы может быть выражена через $L$.
$\pi(L)=TR(L)-TC(L)$
Такую функцию прибыли можно максимизировать по $L$.
$\pi'(L)=TR'(L)-TC'(L)=MRP_L-MC_L=0$
После взятия производной, ее приравнивания к нулю и дальнейшей проверки мы найдем, какое количество труда фирме выгодно будет нанять для максимизации своей прибыли
$MRP_L$ - это предельный доход труда в денежном выражении. Показывает доход, полученный фирмой при найме дополнительного работника.
$MC_L$ - предельные издержки труда, затраты фирмы на найм дополнительного работника.
На рынке труда могут встречаться совершенно различные рыночные структуры.
Сравним совершенно конкурентный рынок труда с монополизированным, где работает профсоюз (действия профсоюза эквивалентны действиям монополиста).
$L_D=1000-w$, $MC_L=-200+w$ (В ск $L_S$), найти оптимальное количество нанимаемого труда на совершенно конкурентном рынке данного фактора производства и на монополизированном.
Совершенная конкуренция:
Равновесие на совершенно конкурентном рынке труда достигается также как и на совершенно конкурентном товарном рынке - в точке пересечения кривой спроса с кривой предложения.
$1000-w=-200+w$
$w_{ск}=600$
$L_{ск}=400$
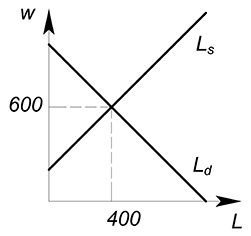 Профсоюз:
Профсоюз:
Спрос на труд предъявляют фирмы, максимизирующие свою прибыль, профсоюз, выступающий со стороны продавцов, также максимизирует свою прибыль.
$L_D=1000-w$
$w=1000-L_D$
$TR(L)=w(L)\cdot L=1000L-L^2$
$MRP_L=TR'(L)=1000-2L$
$MRP_L=MC_L$
$1000-2L=L+200$
$L=\dfrac{800}{3}$
Выполним проверку:
$\pi'(L)=MRP_L-MC_L=800-3L$
$pi''(L)=-3$
$-3 < 0$, следовательно в точке экстремума находится максимум функции.
Таким образом:
$L_{мон}=\dfrac{800}{3}$
Подставляем полученное значение в функцию спроса на труд:
$w_{мон}=\dfrac{2200}{3}$
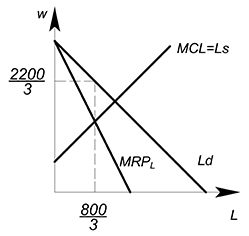
Естественно, у профсоюза как у монополиста нет функции предложения. На графике надпись "$MC_L=L_S$" обозначает, какую кривую надо брать за $MC_L$
$w_{ск} < w_{мон}$
$L_{ск} > L_{мон}$
Задачи
| Задача |
|---|
| Труд |
| Силиконовая деревня |
| Мигранты |



 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ