1.6 Вычисление площадей с помощью интеграла

В задачах по экономике иногда для успешного их решения необходимо найти площадь под графиком функции — площадь криволинейной трапеции.

Определение 1
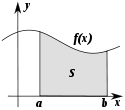
Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке $[a;b]$ функции $f$, осью $Ox$ и прямыми $x=a$ и $x=b$.

Теорема
Пусть $f$ является непрерывной и неотрицательной на отрезке $[a;b]$ функцией, а $S$ — площадью соответствующей криволинейной трапеции. Если $F$ есть первообразная для $f$ на интервале, содержащем отрезок $[a;b]$, то $S=F(b)-F(a)$.

Определение 2
Это $F(b)-F(a)$ является приращением первообразной $F$ функции $f$ и называется интегралом от $a$ до $b$ функции $f$.

Если $F'=f$, то
$\int\limits_a^b{f(x)}dx=F(b)-F(a)$

Это неравенство называется формулой Ньютона-Лейбница.

Таким образом, формулу для вычисления площади криволинейной трапеции можно записать следующим образом:

$S=\int\limits_a^b{f(x)}dx=F(b)-F(a)$