Одним чудесным весенним вечером Юный Экономист совершил необычайное окрытие! Он доказал, что правило $MR = MC$ порой не только не обеспечивает нам максимальный уровень прибыли, но и даже не минимизирует убытки. И это при том, что кривая $MR$ строго убывает, а $MC$ имеет привычный $v$-образный вид!
В доказательстве он привел график и вычисления:
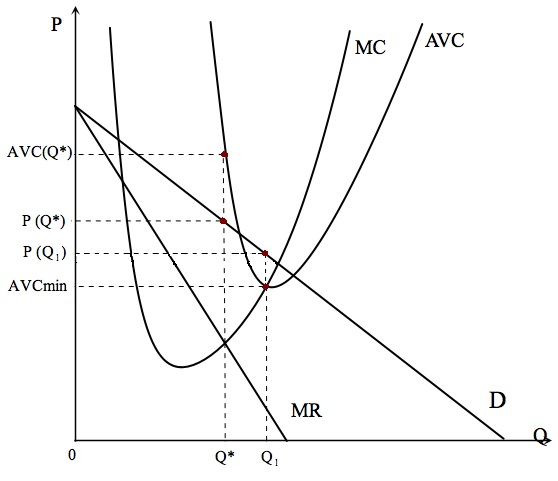
В доказательстве он привел график и вычисления:
$$\pi(Q) = TR - TC = p(Q)*Q - AVC(Q)*Q - FC = (p(Q) - AVC(Q))*Q - FC$$
$$Q = Q^* \Rightarrow \pi(Q^*) = (p(Q^*) - AVC(Q^*))*Q^* - FC < -FC $$
$$Q = Q_1 \Rightarrow \pi(Q_1) = (p(Q_1) - AVC_(min))*Q_1 - FC > -FC $$
$$\pi(Q^*) < -FC < \pi(Q_1)$$
Следуя правилу $MR = MC$, мы не только не максимизируем прибыль, но и рискуем вообще уйти с рынка! $\Rightarrow$ $MR = MC$ не работает!
Прав ли Юный Экономист?
Факультет экономических наук НИУ ВШЭ
Комментарии
Тогда VC - возрастающая функция. но $VC(Q*) > VC(Q1)
Получается, что такой график AVC не существует
Площадь синего прямоугольника больше площади зеленого $\Rightarrow VC(Q*) > VC(Q_1)$
UPD: Однако такое рассуждение будет правильным, только если принять, что $MC$ изображена верно)
В любом случае, добавление условия про $TC$ изменит лишь формулировку окончательного ответа.
думала о площади между графиками. как раз TR-TC. вроде все-таки нормально
Теперь пользуемся определением определенного интеграла: $ \pi(Q_3)-\pi (Q_2) =\int_{Q_2}^{Q_3}(\MR(Q)-\MC(Q))dQ < 0 $( $FC$ уйдут ) - противоречит условию $\pi(Q_2)=\pi(Q_3)=-\FC$. Отсюда вывод, что т.к. интеграл не наврет, значит, $\MC(Q)$ не соответсвует $\AVC(Q)$.