Однажды Юный экономист получил от Старого экономиста в школе задание: нарисовать в координатах APL(L), MPL(L) совершенно конкурентную как на рынке конечной продукции, так и на рынке труда (единственного используемого фактора) фирму. "Да ну, это же проще пареной репы", - подумал Юный экономист и быстренько намалевал представленный здесь график. Каково же было его негодование, когда на следующий день он увидел в своей тетрадке жирную двойку. "Совсем спятил старый дурак!" - процедил сквозь зубы Юный экономист и побрёл домой.
Справедливо ли была поставлена оценка?
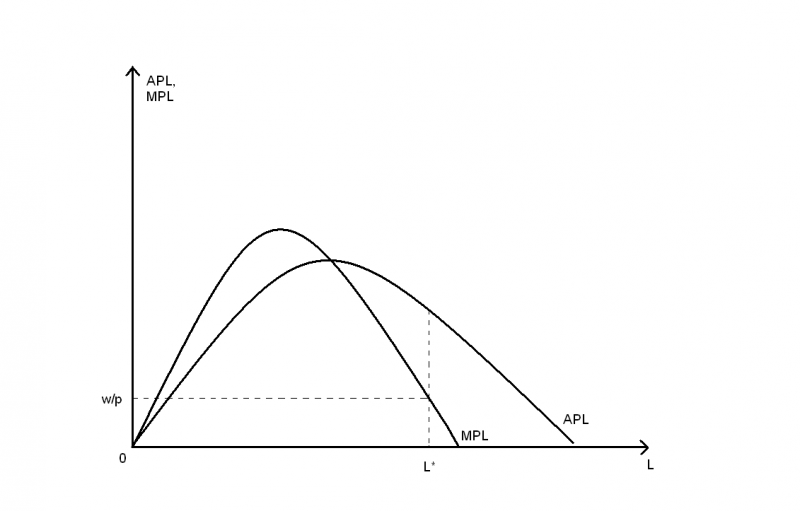
Справедливо ли была поставлена оценка?
Файлы:
Факультет экономических наук НИУ ВШЭ
Комментарии
С другой стороны, зная график средней величины, можно найти максимум этой самой величины.Для этого нужно провести касательную к графику AP из начала координат, в этой точке эластичность AP по L равна единице, а значит эластичность TP по L рава нулю, что говорит нам о том, что в этой точке MP должно равняться нулю.Но на графике эти две точки не совпадают!
1) Можно поставить под сомнение тот факт, что кривые $AP_L$ и $MP_L$ выходят из начала координат, а не из какой-то более высокой точки на вертикальной оси.
2) Можно также придраться к тому, что Юный экономист прорисовал график $AP_L$ дальше точки, в которой $MP_L=0$, что бессмысленно, ибо фирма никогда не будет нанимать такое количество труда (но это совсем уже занудство...).
И всё равно, даже вместе, эти варианты как-то не тянут на двойку... :)
Продлим график MP до того L, где TP равен нулю.Тк функция среднего значения не имеет изломов/перегибов, то производня общей функции непрерывна.
Примем L=5 в точке, где MP=0 и L=7, где TP=0.Тогда площадь между графиком MP и осью абцисс на промежутке от 5 до 7 должна примерно равняться 10 (изменению функции).Судя по графику, это невозможно
В любом случае, ошибка гораздо более существенна.