Рассмотрим некоторые множества A и B, и некоторое правило, которое каждому элементу из A ставит в соответствие ровно один элемент из B. Это правило называется функцией (другое название функции – отображение).

Например, A – множество книг, B – множество натуральных чисел, а функция f ставит в соответствие каждой книге количество страниц в ней. Пусть мы имеем некоторую книгу x. Фраза y=f(x) означает, что y – это количество страниц в книге x. Посмотрев на определение функции f, мы понимаем, что y обязательно будет натуральным числом, т.к. y должен принадлежать B.

Множество A имеет название – область определения функции. Множество B не имеет устоявшегося названия; я слышал название "область прибытия": мы "отправляемся" из множества A и "прибываем" в множество B (по аналогии множество A можно называть "областью отправления", но "область определения" – более распространённое название).

Когда определяют функцию, пишут так:
$f: A\to B, f(x)=\dots$, где вместо многоточия описано правило – как по данному нам элементу множества A найти элемент множества B, который ставит ему в соответствие данная функция. Множество A необходимо в определении функции: мы должны знать, что можно "подставлять" в функцию, а что нет. Одного правила тут недостаточно: например, запись f(x)=2x может означать в 2 раза большее число, если x – это число, или в два раза более длинный вектор, смотрящий туда же, куда и x, если x – это вектор. Что касается области прибытия, то по комбинации области определения и правила можно, в общем-то, самому догадаться о том, какова область прибытия, но, тем не менее, область прибытия часто указывают в явном виде для пущей ясности. Кроме того, часто правило вообще до поры до времени не указывается, а задаются только области определения и прибытия и рассматривается целый класс функций, переводящий элементы из первой области во вторую (см., например, раздел про непрерывность чуть ниже).

В школе в основном работают с числовыми функциями числового аргумента, и области определения и прибытия часто опускают, подразумевая, что всем понятно, какие они.

Отметим, что область (фактически принимаемых) значений функции f (множество всех y, таких что y=f(x) хотя бы для одного x из области определения функции f) не обязана совпадать с областью прибытия. Например, $f: \mathbf{R}\to\mathbf{R}, f(x)=x^2$: области определения и прибытия совпадают со множеством действительных чисел $\mathbf{R}$; область значений – это множество неотрицательных чисел (обозначается $\mathbf{R}_+$). $\mathbf{R}_+\subset \mathbf{R}$, но $\mathbf{R}_+\neq \mathbf{R}$

До кучи добавлю, что множество положительных чисел обозначается $\mathbf{R}_{++}$. $\mathbf{R}_{++}=\mathbf{R}_+\setminus\{0\}$

В определении функции сказано, что каждому элементу из области определения должен соответствовать ровно один элемент из области прибытия. Рассмотрим следующий рисунок:

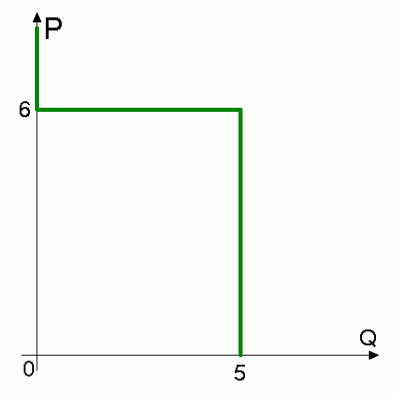
Зелёную линию нельзя считать графиком функции из $ \mathbf{R}_+ $ в $ \mathbf{R}_+ $. В то же время в экономике сплошь и рядом возникают подобные ситуации. Например, при каждой возможной цене некоторого товара потребитель решает, сколько он хочет купить этого товара. При этом вполне возможно, что при какой-то цене ему будет безразлично, купить одну или две единицы этого товара, или любое количество от 0 до 5, как на нашем рисунке. Фактически функция спроса нашего потребителя – это отображение из области неотрицательных чисел (эти числа – цены) в множество всех подмножеств множества неотрицательных чисел (эти числа – количества товара). То есть каждой цене функция спроса ставит в соответствие целое множество количеств, каждое из которых при данной цене потребитель оценивает не хуже других; вот наша функция и отображает в множество всех таких множеств. Это изображено на нашем рисунке: каждой цене соответствует ровно одно подмножество множества $\mathbf{R_+}$. При всех ценах, не равных 6, это подмножество состоит из одной точки, а при $P=6$ это отрезок $[0;5]$. Таким образом, на рисунке изображён график функции, но её областью прибытия является не $\mathbf{R_+}$, а множество всех подмножеств $\mathbf{R_+}$.

Числовые функции одной переменной

Рассмотрим функции, определённые на некотором подмножестве числовой прямой (т. е. множества действительных чисел). Например, это может быть некоторый промежуток.

(5;10] – множество всех чисел, больших 5, но меньших либо равных 10. Круглая скобка означает, что конец не включается в промежуток, а квадратная – что включается. Напомню специальные названия промежутков:

(5,10) – интервал от 5 до 10

[5,10] – отрезок от 5 до 10

Непрерывные функции

Представьте, что мы варим суп. Нас интересует вкус того, что у нас получится. Вкус – комплексная штука; одним из его компонентов является солёность (в данном случае я имею в виду именно вкусовые ощущения, а не процентное содержание соли). Мы не хотим, чтобы суп был недосоленный или пересоленный; есть некоторый оптимальный с нашей точки зрения уровень солёности. Мы не можем задавать его непосредственно (мы даже не знаем, в чём он измеряется), но мы можем влиять на него, выбирая объём соли, которую мы добавляем при варке. Солёность есть функция от объёма соли.

Пусть в рецепте написано "20 г соли". Мы бы рады положить ровно 20 г, но мы неизбежно наберём соль с некоторой погрешностью, даже если будем использовать весы. Например, мы положим 20,5 г соли. Почему суп будет таким же вкусным, как и ровно при 20 г? Потому что солёность супа зависит от объёма соли непрерывно: если немного изменить величину аргумента, значение функции изменится тоже на немного. Но что такое "немного"? В данном случае полграмма – достаточно малое изменение (для того чтобы мы не заметили разницы). Однако вполне могло быть так, что мы не замечаем отклонения только в 0,1 г, а отклонение в полграмма уже делает суп невкусным. Непрерывность функции всё равно позволит нам поесть вкусно, если мы возьмём более точные весы; мы подошли к тому, чтобы ввести точное определение непрерывности.

Рассмотрим некоторую функцию $f: A\to \mathbf{R}$, где $A\subset \mathbf{R}$. Рассмотрим некоторую точку $x\in A$.

Нам понадобится понятие окрестности. Окрестностью точки x радиуса $\varepsilon$ называется множество точек, отстоящих от точки x строго меньше, чем на $\varepsilon$. Когда мы находимся на числовой прямой, то это просто интервал $(x-\varepsilon;x+\varepsilon)$; если бы мы были на плоскости, то эта окрестность была бы внутренностью круга радиуса $\varepsilon$ с центром в точке x.

Так вот, функция f непрерывна в точке x, если, какую бы окрестность числа f(x) мы ни взяли, всегда найдётся такая окрестность точки x, что если x не выйдет за пределы этой второй окрестности, то и значение функции не выйдёт за пределы первой.

Пример. Пусть y – солёность, x – соль; y=f(x). Пусть f(20)=100 (каких-то единиц солёности).

– Хочу, чтобы солёность отличалась от 100 не больше чем на 10.
– Тогда соли с точностью до 0,5 граммов.
– А теперь хочу, чтобы солёность отличалась от 100 не больше чем на 0,1.
– Тогда придётся проследить, чтобы объём соли отличался от 20 не больше чем на 0,0001 грамма.
...

Непрерывность функции позволяет такому диалогу продолжаться бесконечно. Представим, что было бы, если бы непрерывности не было. Например, если объём соли хоть чуть-чуть больше 20, то солёность сразу прыгает до 150. Тогда, какую бы окрестность точки 20 мы ни взяли, мы всегда рискуем получить пересол.

Рассмотрим более реалистичный пример отсутствия непрерывности. Представьте, что вы планируете открыть кинотеатр, и хотите построить функцию общих издержек в зависимости от продолжительности показа фильмов. Если продолжительность показа равна нулю, то вы можете не строить кинотеатр, и тогда издержки равны нулю. Если же вы хотите показывать фильмы хоть сколько-нибудь минут, то необходимо построить кинотеатр. Общие издержки будут как минимум равны постоянным издержкам на строительство кинотеатра при любом положительном уровне выпуска, в то время как при нуле они равны нулю. Взгляните на определение непрерывности и убедитесь, что издержки не непрерывны в нуле (иными словами, они разрывны в нуле).

Другой пример разрывности: зависимость полезности сноубордиста (или другого экстремала) от степени экстремальности (например, от скорости, с которой он съезжает с горы): до поры до времени чем экстремальнее, тем лучше, и небольшое увеличение экстремальности приведёт к небольшому изменению полезности, но как только достигнут уровень экстремальности, при котором сноубордист уже не может справиться с управлением и сворачивает шею, то полезность делает скачок вниз (функция полезности терпит разрыв в этой точке).

Когда мы хотим схематично изобразить график числовой функции одного числового аргумента, то, если эта функция непрерывна, мы можем сделать это, не отрывая карандаша от бумаги.

Если функции $f$ и $g$ непрерывны в некоторой точке $x_0$, то непрерывными в этой точке будут также сумма и произведение этих функций. Если вдобавок $g(x_0)\ne0$, то непрерывным в этой точке будет и частное функций $f$ и $g$, т.е. функция $h$, такая что для любого $x$ из области её определения выполняется: $h(x)=f(x)/g(x)$. Если функция $g$ непрерывна в точке $x_0$, а функция $f$ непрерывна в точке $g(x_0)$, то в этой точке будет непрерывной композиция функций $f$ и $g$, т.е. функция $h$, такая что для любого $x$ из области её определения выполняется: $h(x)=f(g(x))$ (другое название композиции — сложная функция). Эти свойства довольно интуитивны, если вспомнить определение непрерывности. Довольно просто можно доказать их строго.

Функция f называется непрерывной на множестве A, если она непрерывна в каждой точке множества A.

Монотонные функции

Монотонные функции – возрастающие или убывающие.

Пусть функция f определена на множестве $X\subset R$. Рассмотрим $A\subset X$.

Функция f называется строго возрастающей на A, если для любых $x_1,x_2\in A$ таких, что $x_2>x_1$, выполняется: $f(x_2)>f(x_1)$.

Функция f называется нестрого возрастающей (неубывающей) на A, если для любых $x_1,x_2\in A$ таких, что $x_2>x_1$, выполняется: $f(x_2)\ge(x_1)$.

Упражнение: сформулируйте по аналогии определения строго и нестрого убывающих функций.

Чтобы лучше усвоить какое-то свойство, полезно подобрать примеры объектов, которые:
а) удовлетворяют ему;
б) не удовлетворяют ему;
в) почти удовлетворяют (ну или удовлетворяют на первый взгляд), но всё-таки не удовлетворяют (если посмотреть внимательно);
г) почти не удовлетворяют, но всё-таки удовлетворяют.

Я оставляю это дело вам. Не забудьте поделиться интересными примерами с коллегами.

Предел функции

Рассмотрим функцию
$f(x)=\begin {cases}x^2, если x<2 \\x^2+1, если x\ge 2\end {cases}$

Нарисуйте её график. Представьте, что мы движемся по оси x слева направо, приближаясь к точке x=2, но всё время оставаясь левее её. При этом нас интересует то, как ведут себя при этом значения функции, т. е. f(x). По графику видно, что если x будет приближаться к 2 слева всё больше и больше, то f(x) будет всё ближе и ближе к 4. Какую бы маленькую окрестность числа 4 мы ни взяли, мы всегда сможем найти такую окрестность точки 2, что если x не выйдет за пределы этой второй окрестности, при этом оставаясь строго левее 2, то и f(x) не выйдет за пределы первой (убедитесь в этом с помощью построенного вами графика). Это определение того, что предел функции f при x, стремящемся к 2 слева, равен 4. Обратите внимание, что само значение функции в точке 2 не влияет на предел слева; он описывает, что происходит с функцией, если мы неограниченно приближаемся к точке 2, но всё же никогда её не достигаем. При x<2 наша функция ведёт себя одним образом, а ровно в точке x=2 с ней что-то происходит, и после этого она ведёт себя уже другим образом. Предел слева описывает первую часть жизни нашей функции, и его не заботит вторая:)

Аналогично, предел справа равен 5. В данном случае он совпадает со значением функции в точке x=2. Но можно легко представить и такую ситуацию:
$f(x)=\begin {cases}x^2, если x<2 \\10, если x=2\\x^2+1, если x> 2\end {cases}$

Мы изменили значение функции в точке x=2, но предел слева в этой точке по-прежнему равен 4, а предел справа по-прежнему равен 5.

Говорят, что функция имеет предел в точке x, если в этой точке существуют и равны друг другу оба односторонних предела (т. е. пределы слева и справа).

$f(x)=\begin {cases}x^2, если x<2 \\10, если x=2\\x^2, если x> 2\end {cases}$

В данном случае предел функции f при x, стремящемся к 2, равен 4. Это обозначается так: $\lim\limits_{x\to 2}f(x)=4$. При этом $f(2)=10\neq \lim\limits _{x\to 2}f(x)$

Функция f непрерывна в некоторой точке a, если она имеет в этой точке предел, равный её значению в этой точке: $f(a)=\lim\limits _{x\to a}f(x)$. Убедитесь в том, что это соответствует определению непрерывности, которое было дано выше.

Мы рассматривали то, как ведёт себя функция при неограниченном приближении к некоторой конечной точке. Но кроме того, часто интересно изучить, как ведёт себя функция, если неограниченно увеличивать x (записывается $x\to +\infty$). Например, $\lim\limits _{x\to +\infty}\frac1x=0$: какую бы окрестность числа 0 мы ни взяли, всегда найдётся такая "окрестность плюс бесконечности" (так мы назовём множество чисел, больших некоторого заданного числа), что если x не выйдет за пределы этой второй окрестности (то есть мы будем брать достаточно большие иксы – большие того самого заданного числа), то и значение функции не выйдет за пределы первой.

Функция $f(x)=sin(x)$ не имеет предела при $x\to +\infty$: что бы мы ни подставили вместо числа 0 в только что написанное определение, мы не получим верного утверждения (убедитесь в этом).

Дифференцируемые функции

Самая простая функция (ну, кроме константы) – линейная, т. е. $f(x)=kx+b$, где k и b – некоторые заданные числа, параметры. Её и нарисовать просто, и посчитать значение в любой точке. С нелинейными это делать гораздо сложнее, но жизнь упрощается, если можно строить касательные к графику данной функции. Касательная к графику функции в некоторой точке – это такая прямая, что если рассматривать график функции во всё меньшей окрестности данной точки (как бы смотреть на него под всё более сильным микроскопом), то график функции будет всё ближе к этой прямой; будет трудно различить их. Например, функция $f(x)=x^2$ в точке $x=0$ имеет касательную $g(x)=0$. Касательная не всегда существует: например, её нет в точке $x=0$ для функции $f(x)=|x|$: какой микроскоп ни возьми, график вблизи нуля будет выглядеть одинаковым клювом, вовсе не похожим на прямую.

Однако в большинстве случаев, с которыми мы имеем дело, касательная существует. Даже у $f(x)=|x|$ она существует во всех точках, кроме $x=0$. Она существует у степенных и экспоненциальных функций, синусов, логарифмов и ещё много у чего.

Так каким образом упрощается жизнь? Если нужно построить график функции в окрестности некоторой точки, мы вместо этого строим касательную. Если окрестность достаточно маленькая, то разница между касательной и настоящим графиком будет незаметная.

Для того чтобы построить касательную в некоторой точке, нужно посчитать значение функции в этой точке, а также угловой коэффициент касательной (k в формуле kx+b). Последний равен значению производной функции f в этой точке. Это вот такой предел:
$\lim\limits _{\Delta\to 0}\frac{f(x+\Delta)-f(x)}{\Delta}$

Мы фиксируем точку x и рассматриваем близкую к ней точку $x+\Delta$ (если $\Delta>0$, то эта точка находится справа от x; если $\Delta<0$, то слева). На графике отмечаем точки с координатами $(x;f(x))$ и $(x+\Delta;f(x+\Delta))$ и соединяем их прямой. Отношение $\frac{f(x+\Delta)-f(x)}{\Delta}$ – это угловой коэффициент этой прямой. Приближая $\Delta$ к нулю, мы рассматриваем всё более близкую (к точке $(x; f(x))$) точку графика функции; каждый раз мы проводим прямую через эти две точки и замеряем её угловой коэффициент. Если последовательность этих угловых коэффициентов имеет предел, равный какому-нибудь числу, то это и значит, что существует касательная в точке x: все достаточно близкие к x точки "почти" лежат на одной и той же прямой – проходящей через точку x с наклоном, равным этому числу.

Если функция имеет производную в точке x, то она называется дифференцируемой в этой точке.

Дифференцируемость – более сильное условие, чем непрерывность. То есть если функция дифференцируема в некоторой точке, то она непрерывна в ней. Несложно доказать это строго, но я приведу лишь простое интуитивное соображение. Дифференцируемость функции в некоторой точке означает, что вблизи этой точки график функции почти неотличим от прямой. Ну а прямая непрерывна:)

Да, чуть не забыл: производная функции f в точке x обозначается $f'(x)$.
$f'(x)= \lim\limits _{\Delta\to 0}\frac{f(x+\Delta)-f(x)}{\Delta}$

Как вычислять производные

К счастью, нет необходимости считать такие пределы вручную. Производные всех элементарных функций уже посчитаны и занесены в таблицу в учебнике алгебры за 10-й класс; все остальные функции, с которыми мы имеем дело, обычно строятся как какая-то комбинация элементарных функций, и их производные вычисляются с использованием правил дифференцирования:

$(u+v)'=u'+v'$
$(uv)'=u'v+uv'$
$(\frac uv)'=\frac{u'v-uv'}{v^2}$
Если $h(x)=f(g(x))$, то $h'(x)=f'(g(x))\cdot g'(x)$

Об именах и обозначениях функций

Когда мы пользуемся какой-то функцией, мы обращаемся к ней по имени. Некоторые функции имеют устоявшиеся имена: sin, cos, ln и т. д., и мы не называем другие функции этими именами. Большинство функций, с которыми мы сталкиваемся в повседневной жизни, составлены из этих элементарных функций с помощью четырёх арифметических операций (+,-,*,/) и композиции (типа $sin(cos(\cdot))$). Такие функции не имеют устоявшихся имён (угадайте, почему), и мы присваиваем им переменные имена, то есть имена, которые в одном тексте могут означать одну функцию, а в другом – совсем другую. В большинстве случаев они состоят из одной латинской буквы. Если мы ведём повествование всего об одной функции, то почти всегда мы назовём её буквой f.

Кстати, зачем мы вообще придумываем имена для функций, которые выражаются через другие функции? Подсказка: затем же, зачем мы произносим термины, вместо того чтобы произносить то, что является их определениями.

Как мы помним, функция задаёт правило, с помощью которого мы по данному элементу из области определения узнаём, какой именно элемент из области прибытия функция ставит ему в соответствие. Запись очень проста: если x – элемент области определения, а f – функция, то соответствующий ему элемент области прибытия обозначается f(x). То есть пишется название функции и следом за ним в скобках – аргумент. По-другому: f(x) – значение функции f в точке x.

С помощью этого обозначения удобно задавать правило:
$f(x)=1+x^2$
Глядя на эту строчку, сразу понятно, что нужно сделать с аргументом функции f, чтобы получить значение функции f. Заметим, что когда мы таким образом задаём правило, никакого значения не имеет, как именно мы назовём аргумент: с тем же успехом мы могли написать $f(щ)=1+щ^2$ – это правило задаёт ровно ту же функцию. Важно лишь, что мы используем одно и то же обозначение для аргумента по обе стороны знака равенства. Отсюда следует два вывода.
1) Когда вы определяете правило, нужно слева от знака равенства указывать не только название функции, но и обозначения для аргумента. Иначе, если справа от знака равенства присутствуют несколько букв, часть из которых – аргументы функции, а остальные – просто неизвестные параметры, то читатель не узнает, что есть что. $f(x)=x^y$ и $f(y)=x^y$ – совершенно разные функции: степенная и показательная.
2) Когда вы хотите упомянуть функцию целиком, а не её значение в какой-то точке, то так и говорите: "функция f". Фраза "функция f(x)" избыточна, если не бессмысленна. Если вы не говорите, а пишите, и писать слово "функция" вам неохота, но вы, тем не менее, хотите подчеркнуть, что f – это функция, а не переменная, то можно написать $f(\cdot)$ – так вы добьётесь своей цели и при этом не спутаете функцию с её значением в какой-то точке.

Если $f(x)=x^2$, то $f'(x)=2x$. f' – это функция, которая по заданному x вычисляет наклон функции f в точке x. f' – название этой функции, а f'(x) – её значение в точке x. Заметим, что запись f(x)' означает непонятно что – с точки зрения вышеописанной системы обозначений.

Не следует путать числа (переменные) и функции. Вспомните картинку из школьного учебника: ось x, ось y и кривая, рядом с которой подписано $y=f(x)$. Эта запись означает, что для любой точки (x,y) на этой кривой выполняется следующее соотношение между её координатами: $y=f(x)$. Иными словами, эта кривая – график функции f. На том же рисунке может быть изображена другая кривая, с подписью $y=f'(x)$ – график производной функции f. При этом y – всего лишь переменная, и, скажем, запись $y'$ не имеет смысла, даже если строчкой выше было написано $y=f(x)$.

Иногда переменную и функцию обозначают одной и той же буквой. Пусть у вас есть куча переменных, и каждая из них вычисляется по своей собственной функции. В этом случае, чтобы не запутаться, хочется назвать каждую функцию так, чтобы было понятно, к какой переменной она относится; назвать функции так же, как и переменные – самый короткий по записи способ реализовать это.
Например, буквой Q можно обозначить одновременно и производственную функцию, и объём произведённой продукции. Тогда формула $Q=Q(L)$, содержащая два в общем-то разных Q, будет означать следующее: чтобы найти объём произведённой продукции (переменную Q), нужно взять количество единиц труда, которое мы используем (переменную L), и подставить в функцию Q. Это не страшно, если вы сами не запутаетесь.

Заметим, что для некоторых функций существуют специфические обозначения, не подпадающие под общую форму "название и аргумент в скобках". Функции, названия которых состоят не из одной, а из нескольких букв, часто пишут без скобок: $sin x$ вместо $sin(x)$, $ln x$ вместо $ln(x)$. А некоторые особо модные функции, так вообще обозначаются иначе, чем своим именем: квадратный корень из x = $\sqrt{x}$; перемножение числа 5 n раз = $5^n$; произведение всех натуральных чисел от 1 до n = $n!$. Надо полагать, всё это придумывалось для краткости записи.

Обратная функция

Рассмотрим функцию $f: X\to Y$. Оседлав функцию f, мы из элемента множества X попадём в соответствующий ему элемент множества Y. Чтобы попасть обратно, нам нужна обратная функция.
Функция g является обратной к функции f, если она определена на множестве значений функции f (кто забыл, что это такое, см. выше), и при этом для любого $x\in X$ выполняется: $g(f(x))=x$. Упражнение: доказать, что если g обратна к f, то f обратна к g. (Указание: нарисуйте два кружка – область определения и область значений f – и стрелочками изображайте путешествия между ними). Таким образом, понятие обратной функции симметрично, и говорят, что f и g – взаимно обратные функции.

Функция, имеющая обратную, задаёт взаимно однозначное соответствие между двумя множествами – областью определения и областью значений: мало того, что каждому элементу первого множества ставится в соответствие ровно один элемент второго, так в добавок каждому – свой, уникальный. А значит, по элементу области значений можно точно установить, из какого элемента области определения мы в него пришли.
Не всем функциям повезло. Функция $f(x)=x^2$ не имеет обратной: если значение функции равно 4, то мы не сможем узнать, пришли мы в эту четвёрку из 2 или из -2. Впрочем, если сузить область определения, например, до множества неотрицательных чисел, то функция $f(x)=x^2$ будет иметь обратную.

Как найти обратную функцию? Нужно составить уравнение y=f(x) и решить его относительно x, то есть выразить x через y. Если среди корней уравнения только один будет принадлежать области определения x, то полученное выражение будет обратной функцией.

Рассмотрим $f:R_+\to R_+, f(x)=x^2$. Составим уравнение $y=x^2$. Если $y>0$, то у него два корня: $x=\sqrt{y}$ и $x=-\sqrt{y}$. Из них только первый принадлежит области определения f, поэтому f имеет обратную функцию $g(y)=\sqrt{y}$.

Для функции, обратной к f, общепринято пугающее обозначение $f^{-1}$: если $f(x)=x^3$, то $f^{-1}(x)=\sqrt[3]{x}$. Не путайте это обозначение с обратной величиной: $(f(x))^{-1}=\frac{1}{f(x)}$.

Упражнение: как будут выглядеть графики взаимно-обратных функции, если изобразить их на одном рисунке, откладывая аргумент по одной и той же оси?

Производная обратной функции

Нарисуйте график какой-нибудь дифференцируемой функции и проведите касательную к нему в какой-нибудь точке. Угловой коэффициент этой касательной равен значению производной в точке касания, а ещё он равен отношению абсолютных изменений $\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$ при переходе между любыми двумя точками $(x_1, y_1)$ и $(x_2,y_2)$, лежащими на этой касательной. График обратной функции можно увидеть, если развернуть листочек, посмотрев на него с обратной стороны и поменяв местами вертикальную и горизонтальную оси. Проделайте это (можно мысленно), и вы увидите, что угловой коэффициент касательной к графику обратной функции, равный производной обратной функции в соответствующей точке, будет равен отношению $\frac{\Delta x}{\Delta y}$. Таким образом, $$f'(x)=\frac{1}{{f^{-1}}'(f(x))}$$
Кому лень вертеть листочек, может получить этот результат другим способом. Вспомним, что для любого x выполняется $f^{-1}(f(x))=x$. Рассмотрим функцию $h(x)=f^{-1}(f(x))-x $. Она равна нулю при любом значении x, то есть полностью совпадает с функцией $v(x)=0$. Эти две функции просто одно и то же, а значит, совпадают и их производные. Производная константы – ноль. Приравниваем его к производной h: ${f^{-1}}'(f(x))\cdot f'(x)-1=0$, откуда мы и получаем нужное соотношение.