2.6 Бюджетное ограничение и полезность

Определение 1
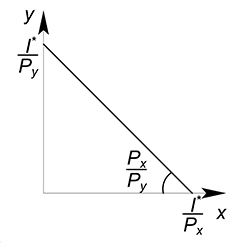
Бюджетное ограничение показывает все наборы товаров, доступные потребителю при данном уровне дохода.

Рассмотрим случай, когда товаров всего 2:

$I=P_x\cdot{x}+P_y\cdot{y}$
В данной формуле I обозначает доход; $P_x$, $P_y$ - цены товаров; $x$, $y$ - их количества.

Определение 2
Пусть потребитель (как обычно) потребляет два товара - x и y. тогда назовем U(x, y) такое число, что чем потребителю лучше от потребления x и y, тем оно больше. если в каких-то двух наборах U совпадает, то для потребителя эти наборы эквивалентны.

Функция полезности показывает зависимость между количеством потребленного товара и полученной от потребления полезностью.

Определение 3
Кривая безразличия показывает все товарные наборы, приносящие потребителю одинаковый уровень полезности.

Пример 1
Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=xy$. Найти оптимальное количество потребления двух благ.

В задачах на данную тему нам необходимо выбрать оптимальную комбинацию потребления товаров, которая будет приносить максимально возможный уровень полезности при заданном уровне дохода. Метод, используемый в задачах данного типа, похож на метод максимизации выручки

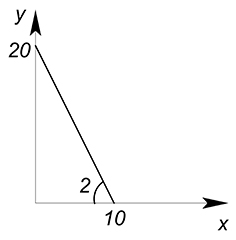
Построим график функции бюджетного ограничения.

$100=10x+5y$

$y=20-2x$

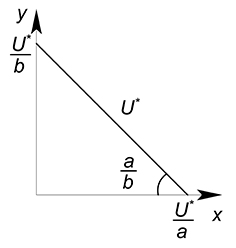
Функция полезности задана уравнением $U=xy$. Зафиксируем переменную $U$ на некотором уровне $U^*$, получим функцию, зависящую от одной переменной $x$:

$y=\dfrac{U^*}{x}$

Изобразив на одном графике бюджетное ограничение и функцию полезности, начнем двигать функцию полезности вверх, пока она не достигнет максимально высокого уровня, то есть, пока прямая бюджетного ограничения не станет касательной к графику функции полезности.

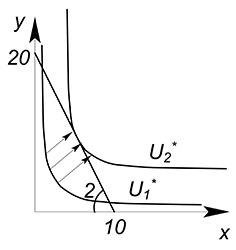
Теперь приравняем производную функции бюджетного ограничения ($y'(x)=-2$) к производной кривой безразличия ($y'(x)=-\dfrac{U^*}{x^2}$).

$-2=-\dfrac{U^*}{x^2}$

$x^2={U^*}{2}$

$x=\sqrt{\dfrac{U^*}{2}}$ (выбираем, естественно, положительный корень)

$y=\sqrt{2U^*}$

Мы получили оптимальные объёмы товаров $x$ и $y$ при данной функции полезности и соотношении цен товаров. Теперь найдем их числовое значение, помня про размер нашего дохода (найдем точку на прямой бюджетного ограничения, дающую максимальный уровень полезности):

$I=10\sqrt{\dfrac{U^*}{2}}+5\sqrt{2U^*}=100$

Решим данное уравнение, получим максимально возможное значение полезности при данном уровне дохода:

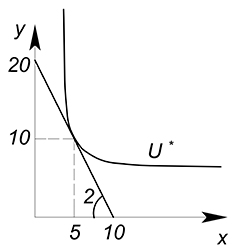
$U^*=50$

Найдем соответствующую ему оптимальную комбинацию $x$ и $y$:

$x=5$

$y=10$

Здесь это можно также решить гораздо проще, если выразить $y$ из бюджетного ограничения и подставить в функцию полезности. Сразу же получится квадратичная парабола.

$U=x(f(x))$, где $f(x)$ - функция бюджетного ограничения.

Пример 2

Если у нас абсолютно взаимозаменяемые (для потребителя не имеет значения иметь единицу $x$ или единицу $y$, если на рынке один из товаров стоит дороже, то потребитель не будет его покупать) товары заменяются друг на друга в постоянной пропорции, вне зависимости от количества благ.

$U=ax+by$

Пропорция всегда постоянна - функция полезности линейна при зафиксированном уровне $U^*$.

Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=x+y$. Найти оптимальное количество потребления двух благ.

Аналогично с задачей 1 построим график функции бюджетного ограничения.

$100=10x+5y$

$y=20-2x$

Дальше будем поступать аналогично случаю, когда КПВ у нас линейная (это ведь тоже бюджетное ограничение), и мы ищем максимально доступную выручку (сейчас максимальный уровень полезности).

Зафиксируем $U^*$, выразим $y$ через $x$:

$y=U^*-x$

Начнем двигать вверх данную прямую, пока она не достигнет максимально высокого положения из вcех возможных.

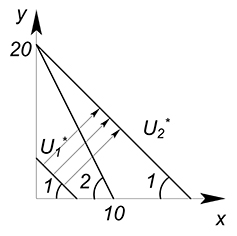
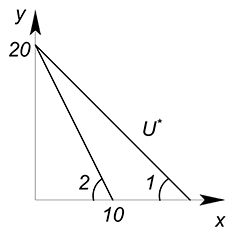
Получим оптимальную точку $x=0$, $y=20$, $U=20$.

Пример 3

Если товары являются взамодополняющими, функция полезности будет иметь вид:

$U=min(ax;by)$

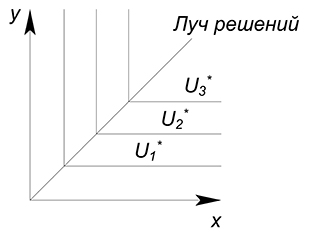
Если товары потребуются только в комплекте, то дополнительная единица одного из благ не принесет увеличения уровня полезности. Увеличение объёма только одного блага бессмысленно, ибо получить больший уровень полезности можно только при пропорциональном увеличении количества обоих благ.

В данном случае решение будет лежать на луче решений, который будет проходить через вершины углов кривых безразличия.

Цена товара $x$ равна 10 д.ед., цена товара $y$ составляет 5 д.ед. Доход равен 100 д.ед. Функция полезности задана уравнением $U=min(x;y)$. Найти оптимальное количество потребления двух благ.

$100=10x+5y$

$y=20-2x$

Функция полезности. Пропорция $x:y$ равна $1:1$, луч решений будет иметь вид

$y=x$

Нарисуем все на одном графике. Будем двигаться вверх вдоль луча решений до точки его пересечения с графиком бюджетного ограничения:

Найдем оптимальные объёмы товаров:

$y=x=\dfrac{20}{3}$

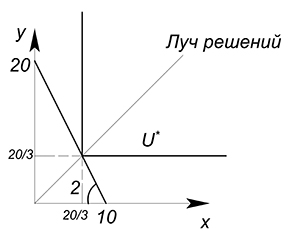
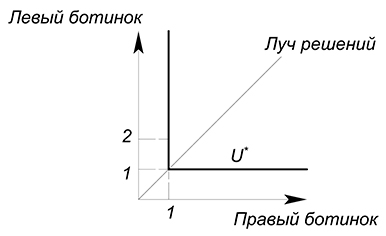
Выше мы рассмотрели случай с пропорцией потребления $1:1$. Такая пропорция подходит, например, для такого товара как ботинки. Если у нас будет 2 левых и 1 правый ботинок, то такая комбинация принесет такой же уровень полезности, как комплект из 1 правого и 1 левого ботинка (если нам доступна комбинация $2+1$, то мы не перейдем на более высокую кривую безразличия, а просто продвинемся вдоль одной из осей старой):

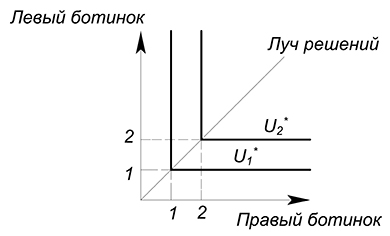
А комплект с пропорциональным увеличением обоих благ уже будет обладать большей полезностью:

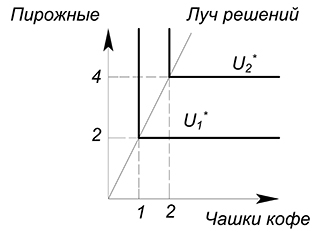
Но вообще пропорции потребления могут быть любыми. Решение тогда все равно будет лежать на луче, проходящем через вершины углов кривых безразличия. Например, можно всегда потреблять комплект 1 чашка кофе + 2 пирожных. Тогда при увеличении количества чашек кофе, нужно пропорционально увеличивать количество пирожных. Если мы купим 1 чашку кофе и 3 пирожных, мы получим тот же уровень полезности, что и когда мы приобретали 1 кофе и 2 пирожных:

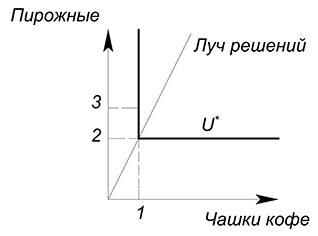
Луч решений будет задаваться функцией $y=2x$, если по оси $x$ отложены чашки кофе, а по оси $y$ - пирожные.