Предположим, что кривые безразличия представляют собой прямые линии с наклоном, равным —b. Как будет выглядеть оптимальный выбор потребителя при заданных произвольных ценах p1, p2 и денежном доходе m?
Решение:Оптимальный выбор составит x1 = m/p1 и x2 = 0, если p1/p2 < b, x1 = 0 и x2 = m/p2, если p1/p2 > b, и любое количество товаров, лежащее на бюджетной линии, если p1/p2 = b .
Я не понимаю, почему сравнивают отношение p1/p2 и b ? Если кливые безразличия в виде прямых линий с наклоном, то это совершенные субституты, правильно?
В книге в отношении совершенных субститутов есть такое объяснение:
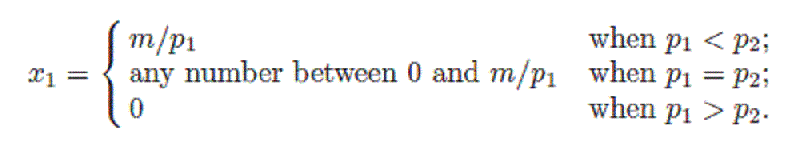
Если p2 > p1, то наклон бюджетной линии менее крутой, чем наклон кривых безразличия. В этом случае оптимальный набор находится в точке, где потребитель тратит все свои деньги на товар 1. Если p1 > p2, потребитель покупает только товар 2. И, наконец, если p1 = p2, существует целый ряд точек оптимального выбора — в этом случае оптимальным будет любое количество товаров 1 и 2, которое удовлетворяет заданному бюджетному ограничению.
Формула для бюджетной линии 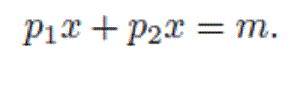

 Факультет экономических наук НИУ ВШЭ
Факультет экономических наук НИУ ВШЭ
Комментарии
Мне конечно понятно, что существуют разные пропорции для товаров субститутов. Но я не понимаю, при чём тут отношение цен и пропорция субститутов? Из чего следует связь между отношением цен и пропорцией субститутов.