б) Занумеруем детей от 1 до 4. Тогда все расселения условно обозначим 12, 13 и 14 — по тому, с кем живёт первый ребёнок. Для каждого примера создадим таблицу, иллюстрирующую его.

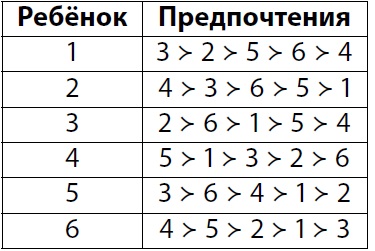
Начнём с единственного стабильного расселения. В примере ниже можно быстро показать, что единственное стабильное расселение это 12. Каждый из соседей в расселении 12 живёт с лучшим для себя, поэтому не хочет меняться. При этом в расселениях 13 и 14 захочет поменяться, например, пара (1, 2).

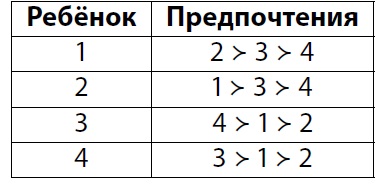
Приведём пример с двумя стабильными расселениями. В этом случае стабильные распределения — это 12 и 14. Заметим, что в расселении 12 есть два ребёнка (1 и 3), которые живут с лучшим для себя соседом, поэтому не будут меняться. Тогда поменяться могут только 2 и 4, но они худшие варианты друг для друга, поэтому меняться не будут. Аналогично, в расселении 14 есть два ребёнка (2 и 4), которые живут с лучшим для себя соседом, поэтому не будут меняться. Тогда поменяться могут 1 и 3, но они худшие варианты друг для друга, поэтому меняться не будут. Расселение 13 не будет стабильным, поскольку захотят поменяться, например, 1 и 2.

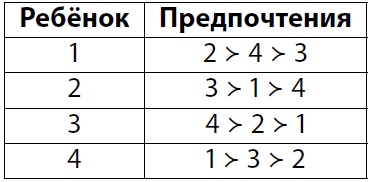
Теперь докажем, что не может быть трёх стабильных распределений. Заметим, что если два человека живут с худшими для себя соседями, то они хотели бы поменяться с кем угодно. Также заметим, что если два человека — лучшие соседи друг для друга, то любое распределение, где они не живут вместе, не может быть стабильным.
Всего есть 3 расселения и 4 человека. Значит, есть хотя бы одно расселение, где сразу 2 человека живут с худшим для себя соседом. Любители комбинаторики могут вспомнить принцип Дирихле.
Если они живут не друг с другом, то они могут поменяться, значит, расселение не стабильно. Если же они живут друг с другом, то один из них может поменяться с кем-то в другой паре, если эта пара не является лучшими соседями друг для друга. Если хотя бы для одного из оставшейся пары сосед не лучший, то он согласится поменяться с кем-то из худших друг для друга соседей, поэтому такое расселение не будет стабильным.
Остался последний случай, при котором эта пара — лучшие друг для друга соседи. Тогда они всегда живут друг с другом в стабильном расселении, значит, остальные расселения не стабильны. Таким образом, 3 стабильных расселения невозможны

в) Рассмотрим предпочтения, описанные в условии.

Шаг 1. Рассмотрим решение индивида i. Если для индивида j он является лучшим соседом, то индивид i не выберет в стабильном расселении никого хуже с его точки зрения, чем j, потому что всегда можно решить жить с j. Учитывая это, вычеркнем невозможные пары. На картинке ниже красным зачёркнуты невозможные пары. Затем те же пары зачёркнуты оранжевым (каждая пара встречается дважды).

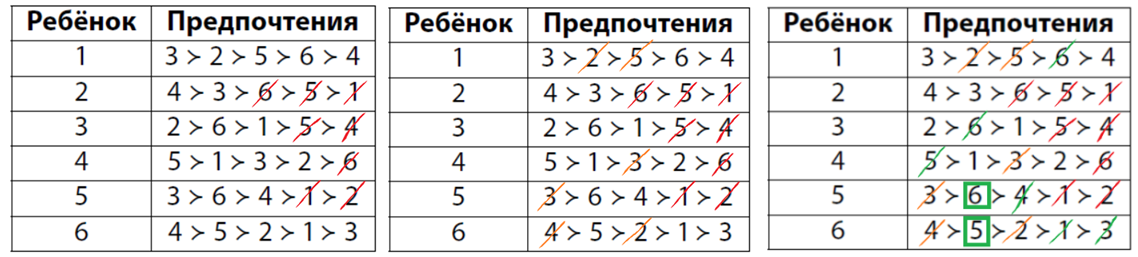
Шаг 2. Заметим, что из оставшихся возможных опций 5 и 6 — лучшие друг для друга (обведено зелёным на картинке). Значит, они будут жить вместе. Тогда зачеркнём зелёным невозможные пары из числа оставшихся.

Шаг 3. Остаётся заметить, что возможны два стабильных расселения оставшихся —13 24 и 14 23. В первом случае 1 и 2 живут с лучшими для себя соседями, а 3 и 4 не готовы меняться. Во втором случае 3 и 4 живут с лучшими для себя соседями, а 1 и 2 не готовы меняться.

Ответ. Всего 2 стабильных расселения —13 24 56 и 14 23 56.

б) Когда выгодно совместно работать? Чтобы понять это, запишем следующее неравенство: время, затраченное при совместной работе, не превышает минимального времени при индивидуальной работе.

$\dfrac{1}{x \cdot (1/2+1/4)}+ \dfrac{1}{x (1/2+1/6)}+1 \leq 2 \Leftrightarrow x \geq \dfrac{17}{6}$

в) Совместная работа становится выгодной при больших значениях $x$, посколько большие значения $x$ соответствуют большему увеличению продуктивности от совместной работы.

г) В качестве верного засчитывался любой обоснованный пример с двумя профессиями, где выгоды от взаимодействия разнятся. Например, в более рутинной профессии (бухгалтер), кооперация вряд ли приносит дополнительные выгоды, поэтому удалённая работа будет скорее полезной. В более творческих профессиях совместное производство идей может быть более эффективным (например, работа учёного-исследователя), поэтому для них переход на удалённую работу скорее снижает производительность.

Мы хотим выбрать $x_2^{2023}$ и $x_3^{2023}$ так, чтобы минимизировать расходы, подсчитываемые по формуле выше.
Заметим, что функция возрастает по $x_2^{2023}$ , поэтому $x_2^{2023} = 0$ .
Относительно же $\sqrt{x_3^{2023}}$ мы получили параболу с ветвями вверх, минимум которой в вершине, т.е.
\[
\sqrt{x_3^{2023}} = 2 \implies x_3^{2023}=4
\]
Тогда $x_1^{2023}=4-2 \cdot 0-2=2$.

Теперь решим задачу для 2024 года. Из функции полезности получим $x_2^{2024}=2-0.5 x_1^{2024}-0.5\sqrt{x_3^{2024}}$. Это выражение подставим в функцию расходов:
\[
Costs^{2024}=10x_1^{2024} + 10 x_2^{2024} + 5x_3^{2024}/2 = 10x_1^{2024} + 10 (2-0.5 x_1^{2024}-0.5\sqrt{x_3^{2024}}) + 5x_3^{2024}/2 =
\]
\[
=20+5x_1^{2024}+2.5 x_3^{2024}-5\sqrt{x_3^{2024}}
\]

Мы хотим выбрать $x_1^{2024}$ и $x_3^{2024}$ так, чтобы минимизировать расходы, подсчитываемые по формуле выше.
Заметим, что функция возрастает по $x_1^{2024}$ , поэтому $x_1^{2024} = 0$ .
Относительно же $\sqrt{x_3^{2024}}$ мы получили параболу с ветвями вверх, минимум которой в вершине, т.е.
\[
\sqrt{x_3^{2024}} = 1 \implies x_3^{2024}=1
\]
Тогда $x_2^{2024}=2-0.5 \cdot 0-0.5=3/2$.

б) Подставим решение из предыдущего пункта. Тогда $Costs^{2023}=30$, а $Costs^{2024}=17.5$. Индекс стоимость жизни $COLI = 17.5/30 \approx 0.58$

в) Рассчитаем оба индекса. Индекс Пааше
\[
I_P = \dfrac{10 \times 0 + 10 \times 3/2 + 2.5 \times 1}{10 \times 0 + 25 \times 3/2 + 2.5 \times 1} = 17.5/40 \approx 0.43
\]

Индекс Ласпейреса
\[
I_L = \dfrac{10 \times 2 + 10 \times 0 + 2.5 \times 1}{10 \times 2 + 25 \times 0 + 2.5 \times 1} = 1
\]

г) Заметим слудеющее соотношение: $I_L \geq COLI \geq I_P$.
Видно, что по индексу Ласпейреса уровень цен не изменился, в то время как по индекс Пааше и COLI упал (наблюдается дефляция).
Это объясняется тем, что при подсчете индекса Ласпейреса фиксируется корзина прошлого года, что не учитывает структурные сдвиги в потреблении индивида.
Индекс Пааше предлагает подстраивать эту корзину под новую из-за чего может происходить переоценка в нижнюю сторону, когда индекс COLI учитывает структурные изменения,
так как напрямую строится исходя из выбора индивида

д) Засчитывались различные корректные объяснения, в частности,

• изменение качества товара,
• малая роль товара в потребления,
• зависимость цены товары от технологического развития,
• роль товара как инвестиции.

В качестве возможного изменения можно учитывать цену за мощность процессоров, величину видеопамяти и т.п. — это позволяет учесть изменение стоимости и доступность технических характеристик во времени. Предложенная идея называется гедонистическое ценообразованием.

б) Эти школьники наиболее похожи на тех, что жил близко к месту инцидента по социально-экономическим и прочим характеристикам, поэтому они служат более вероятным альтернативным сценарием (counterfactual), то есть дают реалистичную картину того, что могло бы случиться со школьниками, живущими в непосредственной близости от инцидентов, если бы этих инцидентов не случилось.

в) В таком случае люди получают информацию об инциденте «из уст в уста», а не через СМИ, что делает роль расстояния до места инцидента ключевой. Более того, медийное внимание может привлечь федеральные власти, которые примут меры по улучшению ситуации, что также может сказаться на результатах.

г) Это осложняет интерпретацию результатов, поскольку добавляется эффект миграции. Если данных по уехавшим школьникам нет, то тогда оценка получается «смещённой»

• Сохранение стимулов у тех работников, которых поощряют. Нельзя стать лучшим навсегда, надо держать планку.
• Не дестимулируются остальные работники — ты проиграл сегодня, но можешь выиграть в следующий раз
• Сохранение уникальности награды как источника мотивации: со временем будет множество Народных артистов, а вот работник месяца всегда один

б) Некоторые примеры

• Финансовые компании. Если сотрудники получают звания за их достижения, то они могут вкладываться в более рисковые активы, чтобы получить более высокий выигрыш и, как следствие, награду.
• Военнослужащие. Исторически, пилоты, например, получают медали за количество сбитых самолетов. Желание получить награду как можно раньше заставляет пилотов заботиться совершать более рискованные атаки.
• Работники тяжелой промышленности. Будучи мотивированными перерабатывать во имя получения признания, работники могут жертвовать своим здоровьем, что увеличивает риски заболеваний и получения травм на работе из-за усталости.

в) Индивидуальные почетные звания поощряют личные достижения и дистимулируют вкладываться в командные задачи. Кроме того, по той же причине, люди в целом меньше вовлекаются в командное взаимодействие,
которое включает в том числе передачу опыта и создание идей, вследствие чего эффективность компании падает. Также из-за тяжести в отделении личного вклада из командного успеха поощрения могут распределяться нечестно (или восприниматься как таковые), что провоцирует конфликты в коллективе

б) Зная значение параметра $a>0$, Саша решает следующую задачу, выбирая $x_1 \in [0; 1]$:
\[
\max\limits_{x_1 \in [0; 1]} (1-x_1) \cdot 240 \cdot (1 + a \cdot x_1)
\]
Это парабола с ветвями вниз, её максимум достигается в вершине, поэтому оптимальное значение
\[
x_1^*=0.5 - 0.5/a
\]
Заметим, что с учётом ограничения на $x_1$ и свойств параболы, для $a\in(0; 1)$ выберем $x_1^*=0$. Поскольку $a>0$, $x_1 \in [0;1/2)$.

в) a — это «награда» за риск. Чем она больше, тем больший риск, начиная с некоторого уровня награды, возьмёт на себя менеджер.

г) Саша решает следующую задачу для $x_1, x_2, x_3\in [0;1]$.
\[
\max\limits_{x_1, x_2, x_3\in [0;1]} 240 \cdot (1+a \cdot x_1) (1-x_1)
+ 240 \cdot (1+x_1+2 \cdot x_2) (1 - x_2)
+ 320 \cdot (1+ x_1 + x_2 + 4 \cdot x_3) (1 - x_3)
\]
Можно решать эту задачу двумя методами. Первый — «школьный» — заметить, что это парабола с ветвями вниз относительно, например $x_3$. Подставить значение вершины, затем вновь заметить, что это парабола с ветвями вниз относительно $x_2$, повторить трюк с вершиной и в конце получить параболу с ветвями вниз относительно $x_1$. Второй способ, к которому могли прибегнуть школьники из математических классов, заключается в том, чтобы приравнять частные производные к нулю и проверить условие второго порядка через гессиан. Такое решение требует достаточного знания математического анализа. Заметим, что от школьников оно не требовалось, хотя и не запрещалось.

Обсудим частую ошибку. Для решения задачи недостаточно сказать, что это парабола с ветвями вниз относительно каждой переменной и решить систему условий первого порядка. Рассмотрим простой контрпример $f(x, y) = -x^2 - y^2 + 4xy$. Следуя такой логике, можно решить, что $(x, y) = (0, 0)$ — это точка глобального максимума функции, что не будет правдой.

При любом корректном решении получим ответ: $x_1=2/3,x_2=1/3,x_3=1/4$.

д) $x_1>x_2>x_3$. Выгодно рисковать в начале, потому что это влияет на будущие выигрыши. Отдача от принятого риска более велика для риска, взятого в первые периоды.

е) Засчитывался любой пример, согласно которому риски в начале выгодны (например, брачный рынок или инвестиции в молодости). Пример должен быть обоснован.