1. Условный потолок
а) (10 баллов) Найдите цены $P^*_A$ и $P^*_B$, которые назначит фирма в отсутствие вмешательства государства.
б) (20 баллов) Президент страны A, ратуя за доступность лекарств, ввел следующее правило: фирма М не может назначать цену в стране A выше, чем в стране B. Теперь фирма М назначает цены так, чтобы прибыль была максимальная с учетом этого правила. Удастся ли президенту с помощью этой меры добиться снижения цены в своей стране?
\(\pi=(30-P_A)\cdot P_A+(10-P_B)\cdot P_B\)
Эта функция – сумма двух не зависящих друг от друга парабол с ветвями вниз, значит, её значение будет максимально, когда максимума достигает каждая из парабол. Это происходит при \(P_A^*=15 \text{ и } P^*_B=5\).
б) В пункте (а) цена в стране A оказалась выше, поэтому максимизировать прибыль так, как раньше, фирма не сможет. Она будет назначать одинаковые цены на двух рынках, то есть фактически столкнётся с общей функцией спроса:
\(Q=\begin{cases} 30-P, & \text{если } 10\leq P\leq 30 \\ 40-2P, & \text{если } 0\leq P\leq10\end{cases}\)
Функция прибыли имеет вид:
\(\pi=\begin{cases} (30-P)P, & \text{если } 10\leq P\leq 30 \\ (40-2P)P, & \text{если } 0\leq P\leq10\end{cases}\)
На первом участке фирма работает только на рынке страны A. Как и в предыдущем пункте, оптимальная цена в стране A при этом равна 15, а прибыль равна 225. На втором участке ($P\leq10$) фирма обслуживает рынки в обеих странах. Парабола $(40 − 2P)P$ имеет ветви вниз и максимум в точке $P=10$, прибыль при этом равна 200, то есть меньше, чем в предыдущем случае. Можно также заметить, что при такой цене фирма ничего не продаёт на рынке страны B, а на рынке страны A не получает максимальной прибыли.
Следовательно, цена в обеих странах будет 15. Таким образом, цена в стране A не изменится, президент своей цели не добьётся.
2. Налог Греты
а) (10 баллов) Определите значение ставки потоварного налога $t$, при котором цена для потребителей вырастет так, как хочет Грета.
б) (10 баллов) Определите значение параметра $\alpha$, при котором верны расчеты экономистов.
в) (10 баллов) Определите значение ставки потоварного налога $t^*$, при котором общественное благосостояние будет максимально.
Для справки. Величина общественного благосостояния при объеме $Q$ здесь равна сумме излишка потребителей (равного $CS=0{,}5Q^2$ д. е.), излишка производителей после уплаты потоварного налога (равного $PS=1{,}5Q^2$ д. е.) и величины налоговых сборов за вычетом вреда от выбросов.
Ответ: t=12.
б) Рассчитаем величину общественного благосостояния до и после введения налога. Налоговые поступления равны $T=tQ$. Графическая иллюстрация представлена ниже:
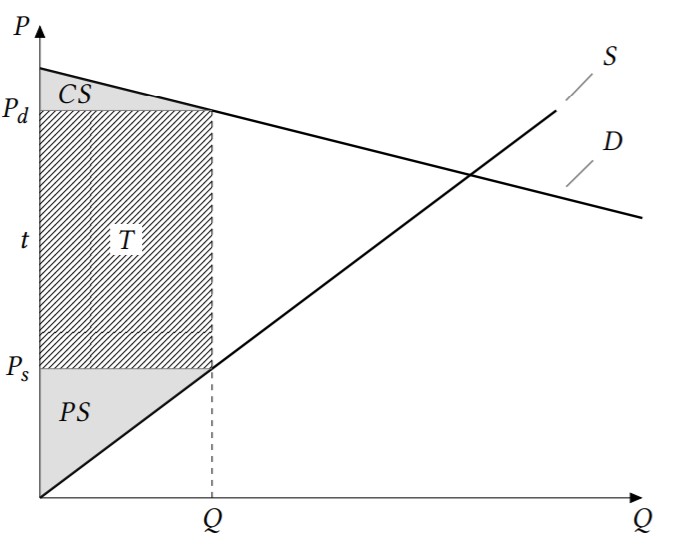
До введения налога объём равен $Q_0=20-15=5$, и величина общественного благосостояния равна:
\(0{,}5Q_0^2+1{,}5Q_0^2+0+\alpha Q_0^2=50-25\alpha\)
После введения налога объём равен $Q-1=20-18=2$, общественное благосостояние составляет:
$0{,}5Q_1^2+1{,}5Q_1^2+tQ_1-\alpha Q_1^2=8+24−4\alpha=32−4\alpha$
Поскольку благосостояние падает на 20%, имеем уравнение $32−4\alpha=0{,}8\cdot(50−25\alpha),$ откуда $\alpha=0{,}5.$
Ответ: $\alpha=\dfrac{1}{2}$
в) Чтобы получить равновесный объем Q, нужно ввести налог по ставке:
$t(Q)=P_d(Q)-P_s(Q)=20-Q−3Q = 20 − 4Q$
Сборы при этом составят $Q\cdot(20−4Q)$. Значит, величина общественного благосостояния при объёме Q составляет:
\(W(Q)=0{,}5Q^2+1{,}5Q^2+Q\cdot(20-4Q)-\alpha Q^2=20Q-2{,}5Q^2\)
Промаксимизируем эту величину по Q, а затем найдем ставку налога t(Q), реализующую этот объём. W(Q) задаёт квадратичную параболу с ветвями вниз, максимум достигается в вершине параболы $Q^*=\dfrac{20}{5}=4$. Этот объём реализует ставка налога $t(4)=4.$
Ответ: $t^*= 4$.
3. Динамика ВВП
а) (8 баллов) Найдите уровень ВВП в долгосрочном равновесии $Y^*$, то есть такой, который, единожды установившись в данной экономике, закрепится и не будет меняться без внешних шоков.
б) (8 баллов) Предположим, что в 2019 году (при $t=2019$) экономика находилась в долгосрочном равновесии. В начале 2020 года правительство реализует стимулирующую фискальную политику и меняет ежегодную величину госзакупок на 10%. Найдите новый уровень ВВП в долгосрочном равновесии $Y^{**}$.
в) (14 баллов) Прежде чем принять значение $Y^{**}$, ВВП будет динамически меняться. Найдите «краткосрочное» значение ВВП, которое будет наблюдаться в 2020 году.
$\begin{array}{c} Y=C+I+G \\ Y=(0{,}6Y+10)+30+60 \\ Y^*=250\end{array}$
б) Поскольку политика стимулирующая, госзакупки должны увеличиться на 10 %, то есть на 6. Составим уравнение с новым уровнем госзакупок:
$\begin{array}{c} Y=(0{,}6Y+10)+30+66 \\ Y^{**}=265\end{array}$
Этот же ответ можно получить, воспользовавшись формулой мультипликатора госрасходов (в которой тоже предполагается постоянный уровень инвестиций):
$\begin{array}{c} \Delta Y=\Delta G\cdot\dfrac{1}{1-mpc}=6\cdot\dfrac{1}{1-0{,}6}=15 \\ Y^{**}=Y^*+\Delta Y=250+15=265\end{array}$
в) Применим формулу ВВП по расходам в 2020 году без предположения о том, что ВВП стабилен:
$\begin{array}{c} Y_{20}=C_{20}+I_{20}+G_{20} \\ Y_{20}=(0{,}6Y_{20}+10)+\bigl(30+0{,}15(Y_{20}-Y_{19})\bigr)+66 \\ Y_{20}=424-0{,}6Y_{19}\end{array}$
Поскольку в 2019 году ВВП равнялся $Y^*=250$, в 2020 году он станет равен: $Y_{20}=424-0{,}6\cdot250=274$.
4. Овощная Страна
а) (3 балла) Предположим, что все овощи потребляются только в тех регионах, где они произведены, распределение салата между жителями внутри региона равномерное. Какое максимальное количество порций салата (комплектов) может ежедневно получать каждый житель региона A?
б) (5 баллов) Ответьте на вопрос предыдущего пункта для жителей региона B.
в) (10 баллов) В Овощной Стране введено центральное планирование. Теперь производство осуществляется так, чтобы суммарное потребление салата в стране было максимальным. При этом комплекты будут распределяться поровну между всеми жителями обоих регионов. Сколько порций салата будет произведено в день?
г) (6 баллов) Будем говорить, что некто проигрывает, если потребление им салата уменьшается. При каких значениях параметра $k \in (0;6]$ жители региона А проиграют от центрального планирования?
д) (6 баллов) Ответьте на вопрос предыдущего пункта для жителей региона B.
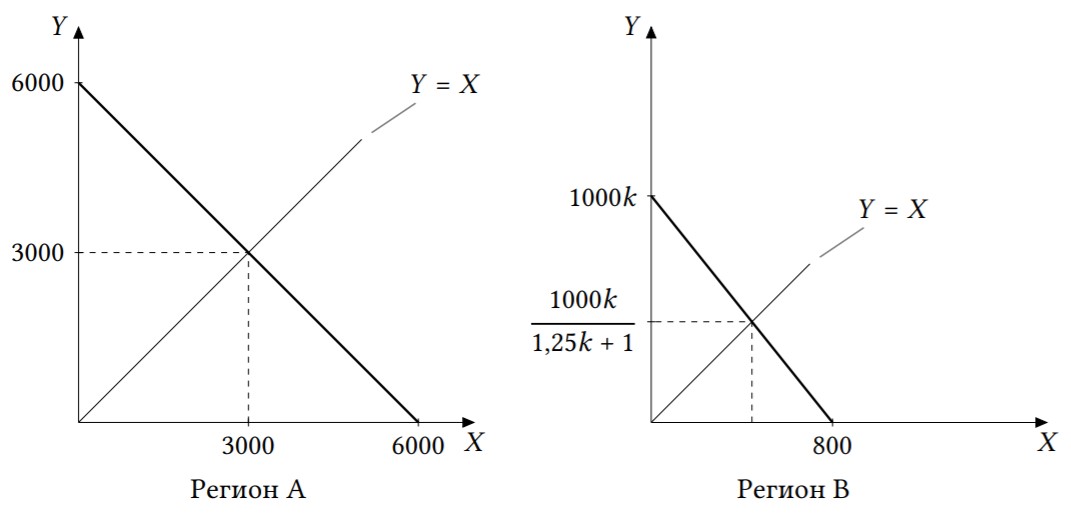
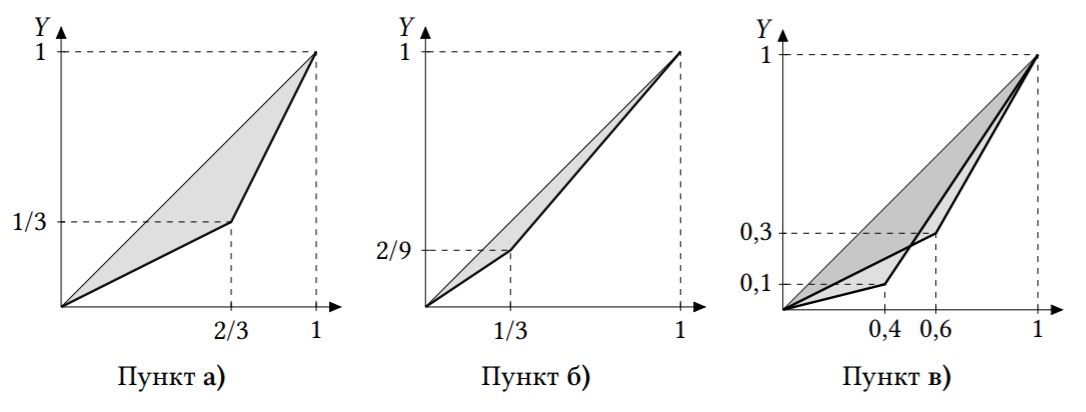
а) Каждый житель может произвести 0,5 кг помидоров и 0,5 кг огурцов соответственно, он и получит 0,5 порции салата. Всего в регионе будет произведено 3000 кг каждого вида овощей, то есть 6000 кг салата. Уравнение КПВ региона имеет вид: $X_A+Y_A=6000$.
б)Пусть $L_X$ – количество работников, занятых производством помидоров, а, $L_Y$ – производством огурцов. Тогда:
\(\begin{array}{ccc} X_B=0{,}8L_X; & Y_B=k\cdot L_Y; & X_B+Y_B=1000\end{array}\)
Уравнение КПВ региона B: $\dfrac{X_B}{0{,}8}+\dfrac{Y}{k}=1000$
Приравнивая $X=Y$, получаем: $Y_B=X_B=\dfrac{1000k}{1{,}25k+1}$
Значит, каждому жителю региона достанется по $k/(1{,}25k+1)$кг помидоров и огурцов, то есть по $k/(1{,}25k+1)$ порции салата (комплектов).
в) Построим суммарную КПВ. Альтернативная стоимость 1 кг помидоров в регионе А равна 1 кг огурцов. Альтернативная стоимость 1 кг помидоров в регионе B равна 1,25k кг огурцов. Вид общей КПВ будет зависеть от соотношения альтернативных стоимостей, то есть от того, $k\leq0{,}8$ или $k>0{,}8$.
Случай 1. $k\leq0{,}8$ (случай k=0,8 можно включить как в случай 1, так в случай 2). Cуммарная КПВ будет иметь вид:
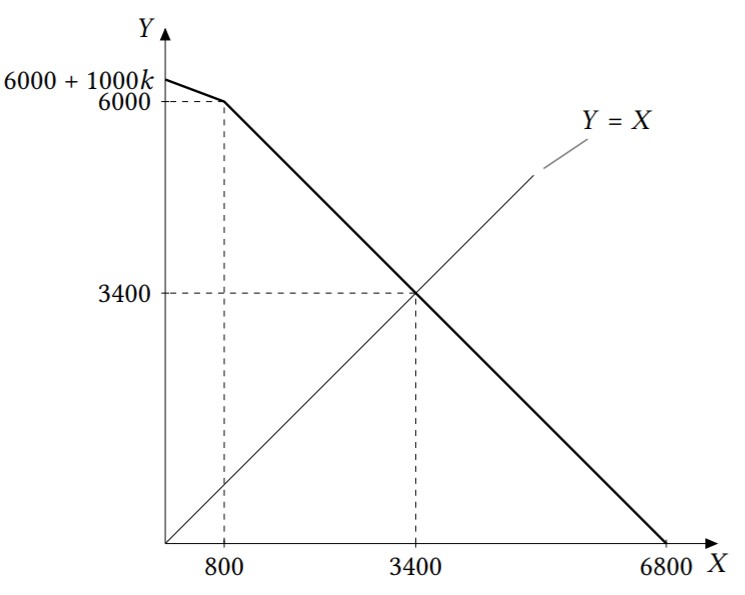
Поскольку 6000/800 > 1, луч $Y=X$ пересечёт её на нижнем участке, имеющем уравнение $Y = 6800 −X$. Значит, $6800-X=X$, откуда $X=3400$. Это и будет суммарноe количество произведённых порций салата.
Cлучай 2. $k>0{,}8$. Cуммарная КПВ будет иметь вид:
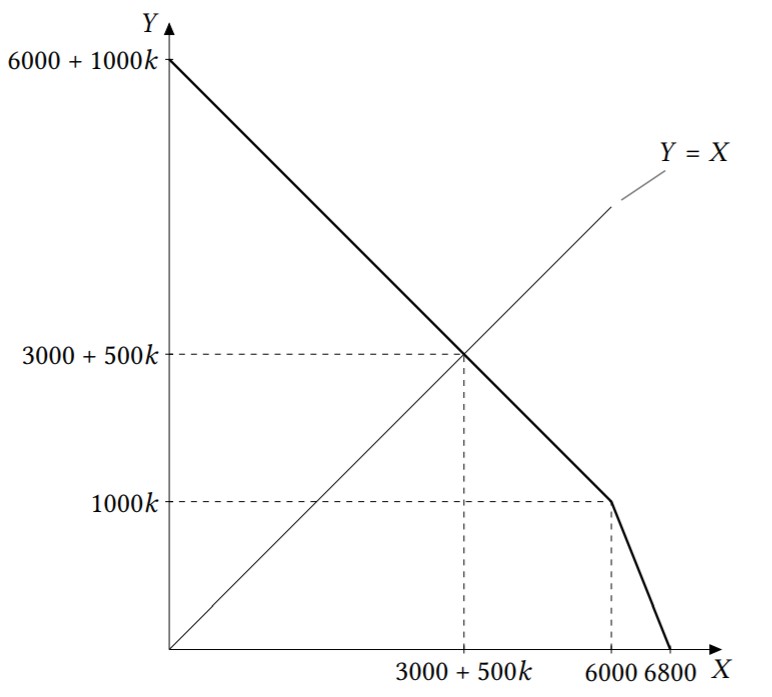
Поскольку по условию $k\leq6$, луч $Y=X$ пересечёт её на верхнем участке, имеющем уравнение $Y=6000+1000k −X$. Значит, $Y= 6000+1000k −X=X$, откуда $X=3000+500k$.
Подытоживая, получаем, что суммарноe количество произведённых порций салата равно:
\(X=Y=\begin{cases}3400, & k\leq0{,}8 \\ 3000+500k, & k \in (0{,}8;6] \end{cases}\)
г) Потребление каждым жителем страны салата при центральном планировании:
\(\dfrac{X}{7000}=\dfrac{Y}{7000}=\begin{cases}\dfrac{17}{35}, & k\leq0{,}8 \\ \dfrac{6+k}{14}, & k \in (0{,}8;6] \end{cases}\)
Поскольку $\dfrac{17}{35}=\dfrac{34}{70}\lt\dfrac{35}{70}=\dfrac{1}{2}$, при $k\leq0{,}8$ жители региона А точно проиграют от планирования. При $k> 0{,}8$ они проиграют, если $\dfrac{6+k}{14}\lt\dfrac{1}{2}$, то есть при $k<1$. Объединяя эти два случая, получаем, что жители страны А проиграют при $k\in(0; 1)$.
д) Аналогичным образом получаем, что при $k\leq0{,}8$ жители страны B проиграют, если $\dfrac{34}{70}\lt\dfrac{k}{1{,}25k+1}$, то есть если $68\lt55k$, что невозможно при $k\leq0{,}8$. Значит, в этом случае они точно не проиграют. Если же $k \in(0{,}8; 6],$ жители страны B проиграют, если: $\dfrac{6+k}{14}\lt\dfrac{k}{1{,}25k+1}.$
После преобразований получаем квадратное неравенство $5k^2 − 22k+ 24 \lt0$. Решением этого неравенства является область между корнями уравнения $5k^2−22k +24 = 0$. Решая уравнение, получаем:
\(k_{1,2}=\dfrac{11\pm\sqrt{121-120}}{5}=\left[\begin{array}{l}2; \\ 2{,}4.\end{array}\right.\)
Поскольку 2,4 < 6, весь интервал (2; 2,4) входит в множество значений параметра, рассматриваемое в данном случае. Значит, весь интервал (2; 2,4) и будет ответом. Жители страны Б проиграют при $k\in(2; 2{,}4)$.