1. GDP — это не всё
- Почему реальный ВВП на душу населения не может выступать в качестве универсального индикатора общественного благосостояния? Что не учитывает этот показатель? Предложите несколько (достаточно четырёх) различных примеров, в каждом случае приведите пояснение.
- Несмотря на то, что американская экономика демонстрирует достаточно устойчивый экономический рост в течение длительного периода времени, нельзя утверждать, что уровень счастья (уровень удовлетворённости жизнью, "happiness") каждого американского гражданина растёт вслед за ростом реальных доходов. Обратимся к графику ниже:
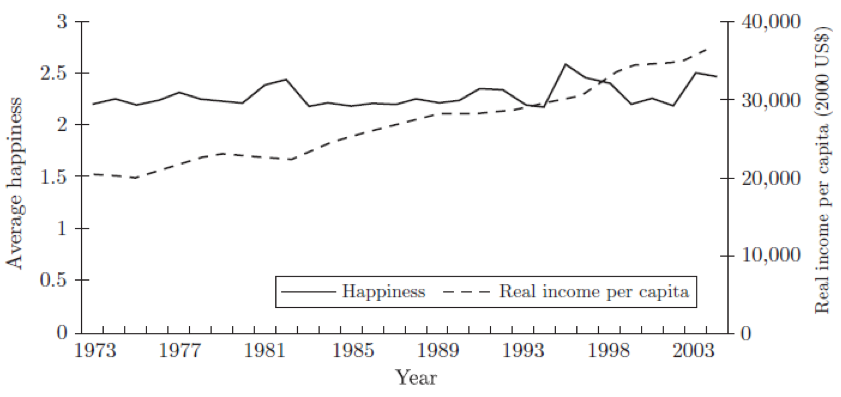
В то время как реальные доходы населения (real income per capita) росли, средний уровень счастья американских граждан оставался относительно постоянным и колебался незначительно. Объясните, почему долгосрочный экономический рост необязательно влечёт за собой увеличение уровня счастья граждан.
- ВВП не отражает изменений в текущей экологической обстановке. Как различные экологические процессы влияют на устойчивый экономический рост? И наоборот, как рост экономики влияет на экологию? Индикатор реального ВВП на душу населения не даёт возможности ответить на эти вопросы, хотя экономисты отмечают, что в большинстве случаев рост экономики сопровождается значительным ущербом, наносимым окружающей среде (загрязнение воды, воздуха, почвы и т.д.), разрушением природного капитала. Таким образом, мы не учитываем тот факт, что рост объёмов производства может повлечь за собой подобные отрицательные экстерналии, снижающие уровень благосостояния граждан: во-первых, неблагоприятная экологическая обстановка оказывает значительное негативное воздействие на здоровье людей, во-вторых, нам приходится инвестировать всё большее количество ресурсов для решения экологических проблем, сокращая свое текущее потребление.
ВВП не учитывает уровень существующего социально-экономического неравенства. Хотя неравенство в рыночной экономике – явление совершенно закономерное, избыточное неравенство является одним из наиболее серьёзных поводов для недовольства населения. Сильная дифференциация доходов в обществе влечёт за собой и неравенство возможностей (порождает неравный доступ для большинства людей к ограниченным и необходимым ресурсам), разрушает социальную сплочённость (как следствие зачастую возникает недовольство существующей политической системой). Реальный ВВП на душу населения не учитывает неравенство: пусть, например, ВВП на душу населения в стране вырос на $x$%. Означает ли это, что в среднем доходы каждого выросли на $x$%, или же они выросли только у самых богатых, а у других выросли в куда меньшей степени или даже сократились? Дать однозначный ответ, используя лишь показатель ВВП на душу населения, трудно: вполне возможно, что крупные доходы получает малая доля людей, в то время как остальные живут за чертой бедности.
ВВП не учитывает свободное время (время досуга), которым располагают люди. Рассмотрим следующий пример. Реальный ВВП на душу населения в стране Х может быть намного больше, чем реальный ВВП на душу населения в стране Y, потому что в стране Х люди работают в среднем на несколько часов больше, чем в стране Y. Однако жители страны Y могут ценить свое свободное время куда выше, чем жители страны X. Поэтому нельзя утверждать, что благосостояние граждан в стране X должно быть больше, чем в стране Y: мы не можем объяснить разрыв в благосостоянии между странами исключительно разницей в уровне реального ВВП на душу населения.
ВВП не учитывает технологический прогресс. Благосостояние граждан определяется не только их материальным благополучием. Важно не только то, каков наш доход, но и то, как мы им можем распорядиться. Увеличение качества жизни обусловлено не только ростом реального ВВП на душу населения, но и существенными технологическими изменениями, появлением инновационных технологий, продуктов.
ВВП не учитывает уровень образования, медицинских технологий. Хотя при расчёте ВВП мы и учтём покупку нового медицинского оборудования или строительство новой школы, оценить качественные изменения с помощью этого индикатора мы не сумеем. Расходы на медицину могут быть высокими, но увеличивается ли продолжительность жизни граждан, качество предоставляемого медицинского обслуживания? Расходы на образование могут расти, но действительно ли повышается качество предоставляемых образовательных услуг?
ВВП не учитывает накопленное богатство и то, как оно изменяется, поскольку является показателем потока.
При расчёте ВВП мы, во-первых, не можем учесть степень вовлечённости граждан в политические процессы (уровень политической активности граждан), во-вторых – предоставляемые гражданские, политические, культурные и социально-экономические права, нарушение и ущемление которых может иметь место.
Приведённые выше примеры – далеко не единственные: участник мог привести и другие (с соответствующими пояснениями).
-
Подобная закономерность впервые была отмечена Ричардом Истерлином в 1974 году в работе Does Economic Growth Improve the Human Lot? Some Empirical Evidence (так называемый парадокс Истерлина). Выделяют два основных объяснения:
- Эффект социального сравнения (social comparison): люди не только оценивают свой абсолютный доход, но и сравнивают его с доходом других людей, некоторой референтной группы (comparison group) – мы счастливее, когда наш доход выше, чем у людей, её составляющих. В референтную группу могут входить, например, друзья, соседи, члены семьи, люди того же пола, уровня образования, обладающие схожими социоэкономическими характеристиками и т.д. Таким образом, важен рост относительного, а не абсолютного дохода (4 балла).
- Эффект адаптации (adaptation mechanism): во-первых, в течение всего жизненного цикла рост реальных доходов сопровождается существенными изменениями в структуре потребностей – происходит переход от удовлетворения более простых, базовых потребностей к более сложным. Поэтому увеличение нашего материального благосостояния даёт всё меньший прирост уровня счастья. Во-вторых, мы оцениваем наши текущие доходы, принимая во внимание доходы предыдущих периодов (что, безусловно, находит своё отражение на нашем субъективном восприятии настоящего и будущего): разовое увеличение дохода делает нас счастливыми лишь на некоторый короткий срок, необходимый для адаптации к новому уровню дохода. Длительное и достаточно стабильное увеличение доходов практически не приумножает нашего счастья, поскольку наш абсолютный доход будет становиться всё больше по сравнению с предыдущими периодами, но относительный остается почти таким же (4 балла).
Конечно, нельзя отрицать наличие положительной корреляции между уровнем реальных доходов на душу населения и уровнем удовлетворённости жизнью, однако подобная взаимосвязь отчётливо прослеживается в основном лишь в краткосрочном периоде, а не в долгосрочном, где, наоборот, подобная взаимосвязь практически не обнаруживается (этот факт также отмечен Ричардом Истерлином в одной из работ 2013 года в ходе исследований «экономики счастья»).
Отметим следующие детали:
- В долгосрочном периоде зависимость между реальными доходами на душу населения и уровнем счастья практически не прослеживается, в краткосрочном она прослеживается куда более отчётливо (см. выше).
- Идея о «точке насыщения» – уровне дохода, начиная с которого прирост счастья индивида становится незначительным (факт, подтверждённый некоторыми эмпирическими исследованиями).
2. Дисбалансы в мировой экономике
- Объясните, что такое счёт текущих операций и почему его профицит позволяет покупать активы других стран.
- На фоне вышеуказанных событий в США все ставки процента (и долгосрочные, и краткосрочные) довольно сильно сократились, что стало беспокоить монетарные власти, поскольку оказывало стимулирующее воздействие на экономику и могло привести к росту инфляции. В ответ на это ФРС начала предпринимать стандартные меры сдерживающей монетарной политики, что непосредственно приводит к росту краткосрочных ставок. Объясните механизм, через который повышение краткосрочной ставки процента могло привести к росту долгосрочных ставок.
- Несмотря на то, что стандартная экономическая логика говорит о том, что долгосрочные ставки должны меняться вслед за краткосрочными, в США ставки по 10-летним облигациям не изменились после повышения ставок ФРС. Объясните, как данное поведение ставок может быть связано с профицитом счёта текущих операций в Китае, странах ОПЕК и других азиатских странах?
- Счёт текущих операций – это один из двух основных счетов платежного баланса любой страны, который отражает все операции, не связанные с куплей/продажей активов, а также с изменением обязательств (эти операции отражаются в счёте движения капитала). Большая часть этого счёта приходится на чистый экспорт, но также туда могут входить денежные трансферты через границу и т.п.
Поскольку в равновесии сальдо платёжного баланса должно равняться нулю, то сальдо счёта текущих операций должно совпадать по величине с сальдо счёта движения капитала, но с противоположным знаком. Соответственно, если в перечисленных странах был такой большой избыток счёта текущих операций, то в них формировался большой отток средств по счёту движения капитала. Последнее может означать не только то, что иностранные инвесторы выводят большое количество средств из данной страны, но ещё и то, что сама страна активно покупает различные иностранные активы либо выдаёт большое количество кредитов иностранным агентам. Собственно, последний канал и говорит о том, что страны с избытком счёта текущих операций покупают активы других стран. - Долгосрочные ставки процента отражают, по сути, ожидания экономических агентов относительно будущей динамики краткосрочных ставок, поскольку людям должно быть безразлично, в какой из активов вкладываться (иначе все переключаются на более выгодный). Соответственно, если текущую ставку по депозитам на один год увеличивают, то и ставка по вкладам, например, на 5 лет, тоже должна увеличиться.
Можно рассуждать следующим образом. Рост краткосрочной ставки привлекает внимание инвесторов к соответствующему типу активов, поэтому они переключаются с долгосрочных активов на краткосрочные. Из-за этого спрос на долгосрочные активы падает, из-за этого цена актива падает, а доходность – растёт. Аналогичное рассуждение могло приводиться не для спроса на активы, а для спроса на кредиты (если краткосрочные ставки растут, то люди будут переключаться с краткосрочных кредитов на долгосрочные, и рост спроса на них приведет к росту ставки процента по данному типу кредитов). - Огромный спрос Китая, ОПЕК и Азии на облигации США привёл к значительному росту их стоимости и снижению ставок. И, несмотря на попытку монетарных властей поднять краткосрочные ставки процента, долгосрочные ставки определялись не столько внутренней ситуацией на рынке активов, сколько спросом других стран (которые, по сути, заинтересованы по большей части в долгосрочных вложениях).
3. Прорыв и стабильность
Пусть $\pi^d$ и $y^d$ — желаемые (desired) уровни инфляции и выпуска в стране Х. Монетарную политику в стране Х осуществляет центральный банк, чьи потери из-за отклонения инфляции и выпуска от желаемых уровней составляют $L = (\pi-\pi^d)^2 + \alpha(y-y^d)^2$. Таким образом, чем дальше уровень инфляции от $\pi^d$ или уровень выпуска от $y^d$, тем хуже центробанку; $\alpha > 0$ — параметр, показывающий, как для центробанка соотносятся потери, связанные с инфляцией и с выпуском.
Известно, что фактические уровни инфляции и выпуска в стране Х в любой момент времени удовлетворяют условию $\pi-\pi^e = \lambda(y-y^*)$, где $\pi^e$ — ожидаемый уровень инфляции, $y^*$ — потенциальный уровень выпуска, $\lambda>0$ — параметр, отражающий, какому отклонению инфляции от ожидаемого уровня соответствует единичное отклонение выпуска от потенциального уровня. Это уравнение принято называть кривой Лукаса.
Центральный банк, минимизирующий свои потери, в рамках своей монетарной политики может выбирать любое значение уровня инфляции, воздействуя на совокупный спрос.
- Разумно было бы считать, что $y^d = y^*$; однако данная модель строится на предпосылке, что $y^d>y^*$. Почему в реальном мире центробанк может желать таргетировать выпуск на уровне выше потенциального? Кроме того, подразумевается, что $\pi^d>0$. Почему современные центробанки обычно таргетируют инфляцию на уровне выше нулевого?
- Какой уровень инфляции $\pi$ установит центробанк в зависимости от ситуации в экономике, т. е. от переменных $\pi^d$, $y^d$, $\alpha$, $\pi^e$, $y^*$, $\lambda$?
- Предположим, что ожидания экономических агентов в стране Х рациональны. Это значит, что агенты знают структуру экономики и функцию потерь центробанка (в том числе знают, чему равны величины $\pi^d$, $y^d$, $\alpha$, $\pi^e$, $y^*$, $\lambda$) и на основе этого способны в точности прогнозировать поведение центрального банка, ожидая именно тот уровень инфляции, который будет «назначен». Стало быть, в равновесии ожидаемый и фактический уровень инфляции совпадут: $\pi=\pi^e$. Какие будут равновесные уровни инфляции и выпуска?
- Допустим, взаимодействие теперь длится не один, а несколько периодов, в каждом из которых потери центробанка и кривая Лукаса имеют одинаковый вид. Инфляционные ожидания теперь формируются иначе: в каждом периоде ожидаемый уровень инфляции равен фактическому уровню инфляции предыдущего периода, т. е. $\pi^e_t = \pi_{t-1}$. Это называется наивные (статические) ожидания. Центробанк «близорукий»: в каждом периоде он минимизирует свои текущие потери, не принимая во внимание предыдущие или следующие периоды. Верно ли, что со временем уровни инфляции и выпуска стабилизируются около каких-то значений? Если да, то каких?
- Интерпретируйте результаты, полученные в предыдущих пунктах. Как найденный уровень инфляции соотносится (меньше/равен/больше) с таргетируемым уровнем? Как найденный уровень выпуска соотносится с таргетируемым и потенциальным уровнем? Почему так, а не иначе?
- $y^d>y^*$. 1) Популизм: в условиях недостаточной автономности ЦБ от органов исполнительной власти на центробанк может оказываться давление со стороны политических властей с целью простимулировать спрос и разогреть экономику (например, накануне выборов). 2) Потенциальный выпуск нельзя назвать общественно оптимальным: при потенциальном выпуске на рынках остаются некоторые искажения (например, наличие стимулирующей безработицы на рынке труда), и если привлечь неиспользуемые ресурсы к делу, то можно увеличить выпуск и благосостояние общества.
$\pi^d>0$. Дефляция опасна по многим причинам, одна из них – стремление потребителей отложить покупки на будущее, поскольку люди ожидают дальнейшего снижения цен. Соответственно, происходит падение потребительских расходов и снижение ВВП. -
Запишем задачу центробанка, выразив выпуск из кривой Лукаса:
$$ L(\pi) = (\pi - \pi^d)^2 +\alpha \left( \frac{\pi - \pi^e}{\lambda} +y^*-y^d \right)^2 \rightarrow \min_\pi $$
Квадратная парабола с ветвями вверх относительно инфляции, вершина в точке
$$\pi = \frac
{\alpha\pi^e + \lambda^2\pi^d + \alpha\lambda(y^d - y^*)}
{\alpha + \lambda^2}$$ -
Подставив $\pi = \pi^e$ в выражение из пункта 2. и преобразовав, получим $\pi = \pi^d + \frac{\alpha}{\lambda}\left( y^d - y^* \right)$.
Напрямую из кривой Лукаса можно получить $y = y^*$. -
На самом деле, уровни инфляции и выпуска стабилизируются при тех же значениях, что и в пункте 3. Вспомним из пункта 2, что
$$\pi_t = \frac{\alpha}{\alpha+\lambda^2}\pi^e_t +
\frac
{\lambda^2\pi^d + \alpha \lambda (y^d - y^*)}
{\alpha+\lambda^2}$$
Обозначим $\frac{\alpha}{\alpha+\lambda^2} = \varphi$, $\frac
{\lambda^2\pi^d + \alpha \lambda (y^d - y^*)}
{\alpha+\lambda^2} = \theta$.
Заметим, что $0<\varphi<1$, и учтем ожидания $\pi^e_t = \pi_{t-1}$, тогда $\pi_t = \varphi\pi_{t-1} + \theta$. Значит,
$\pi_1 = \varphi\pi_{0} + \theta$
$\pi_2 = \varphi\pi_{1} + \theta = \varphi^2\pi_0 + \varphi\theta + \theta$
$\pi_3 = \varphi\pi_{2} + \theta = \varphi^3\pi_0 + \varphi^2\theta +\varphi\theta + \theta$
$\dots$
$\pi_t = \varphi^t\pi_0 + \varphi^{t-1}\theta + \ldots + \theta$.
Если $0<\varphi <1$ и $t \rightarrow \infty$, то $\varphi^t \rightarrow 0$. Значит, по прошествии большого числа периодов, свернув бесконечно убывающую геометрическую прогрессию в скобках, получим
$\pi_t = \theta\frac{1}{1-\varphi}$.
Выполнив обратную замену, получим уровни инфляции и выпуска: $\pi = \pi^d + \frac{\alpha}{\lambda}(y^d-y^*)$, $y = y^*$.
С таким же успехом это можно было увидеть на графике в координатах $(\pi_{t-1}; \pi_t)$, нарисовав график $\pi_t = \varphi\pi_{t-1}+\theta$ и прямую $\pi_t = \pi_{t-1}$. Нарисованный график и показанная на нём динамика – тоже правильное решение (притом более «изящное», чем алгебраическое, приведённое здесь). -
Во-первых, в оптимуме $\pi>\pi^d$, т.е. фактическая инфляция оказалась выше таргетируемой. Перед нами пример, иллюстрирующий динамическую непоследовательность (dynamic inconsistency) низкоинфляционной монетарной политики. Пусть ЦБ объявил, что целевой уровень инфляции равен $\pi^d$. Если бы население поверило ЦБ, то центробанку было бы выгодно установить фактический уровень инфляции выше $\pi^d$, напечатав денег для стимулирования экономики. Однако в реальности центробанку не удастся обмануть население – оно понимает, как поступит ЦБ, и заранее ожидает более высокую инфляцию. Столкнувшись с высокими инфляционными ожиданиями, далее ЦБ уже вынужден печатать деньги, чтобы не пустить экономику в рецессию: если инфляция ниже ожидаемой, то, по кривой Лукаса, экономика падает ниже потенциального уровня.
Во-вторых, в оптимуме $y = y^* < y^d$, т.е. экономика останется на потенциальном уровне, её не удастся разогнать до желаемого уровня, добившись «прорыва». Это видно и напрямую из кривой Лукаса без расчётов, поскольку $\pi = \pi^e$. Действительно, превышение выпуска над потенциальным уровнем означало бы превышение фактической инфляции над ожидаемой, что не является равновесной ситуацией.
4. Максимальный профицит
В 2019 году правительство планирует установить потоварный налог, взимаемый с производителей товара X. Других источников доходов, кроме поступлений в казну от этого налога, у государственного бюджета нет. Также правительство собирается ввести потоварную субсидию, выплачиваемую производителям товара Y. Все расходы государственного бюджета, кроме выплаты данной субсидии, фиксированы и составляют 1000 рублей в год.
- Определите, какого максимального профицита бюджета может достичь правительство в 2019 году в рамках указанной политики при условии, что реальный ВВП страны Альфа в 2019 году по сравнению с 2018 годом должен вырасти на 25 %? При определении реального ВВП считайте 2018 год базовым.
- Из каких соображений, помимо упомянутых в условии задачи, может исходить правительство при определении величины дефицита/профицита государственного бюджета?
-
При введении потоварного налога на рынке товара Х равновесие будет определяться системой уравнений $400 - 2p_x^d = 2p_x^s$ и $p_x^d - p_x^s = t$.
Далее находим равновесный выпуск $x = 200-t$.
Налоговые поступления составят $T = tx = 200t-t^2$.
При введении потоварной субсидии на рынке товара Y равновесие будет определяться системой уравнений $200 - 2p_y^d = 2p_y^s$ и $p_y^s - p_y^d = s$.
Далее находим равновесный выпуск $y = 100+s$.
Расходы на субсидирование составят $S = sy = 100s+s^2$.
Реальный ВВП 2018 года равен $GDP^{18}_{real} = 100\cdot 50 + 110\cdot 100 = 16000$.
Реальный ВВП 2019 года будет равен $GDP^{19}_{real} = (200-t)50 + (100+s)100 = 20000 - 50t + 100s$.
По условию рост реального ВВП должен составить 25%, тогда $20000 - 50t + 100s = 1.25 \cdot 16000$.
Упростив последнее уравнение, получим $t = 2s$.
Тогда сальдо бюджета будет равно $$T-S-1000 = 200t - t^2 - 100s-s^2-1000 = 300s-5s^2 -1000 \rightarrow \max{s\geqslant 0}.$$
Квадратная парабола с ветвями вниз, вершина в точке $s = 30$, тогда сама величина профицита бюджета составит 3500. - Например, увеличение общественного благосостояния за счёт производства общественных благ или стабилизационная политика.
5. Балансировка бюджета и поддержка населения
Государство обеспокоено обнищанием населения: готовность потребителей внутри страны платить за товар X намного ниже, чем цена на мировом рынке. Государство хочет повысить благосостояние своих граждан, однако лишних денег на это нет, поэтому необходимые средства придётся собирать на этом же рынке. Государство желает добиться того, чтобы внутри страны продавалось как можно больше единиц товара X, поэтому оно вводит потоварную субсидию потребителям по ставке $s$ д. е. за каждую купленную внутри страны единицу продукции. Чтобы финансировать программу субсидирования, государство вводит потоварный налог на экспорт по ставке $t$ д. е. за каждую вывезенную из страны единицу продукции. При этом общая сумма денег, потраченная на предоставление субсидии, не должна превышать сумму, полученную благодаря налогу.
- По какой ставке следует ввести субсидию? По какой ставке следует ввести налог? Сколько единиц продукции будет продаваться внутри страны, а сколько — отправляться на экспорт? Сколько составят расходы на предоставление субсидии и доходы от взимания налога?
- Если бы государство рассматривало только вариант введения потоварного налога на экспорт с целью максимально возможного пополнения бюджета, то по какой ставке следовало бы ввести такой налог?
-
Заметим, что у фирмы предельная выручка на внутреннем рынке убывает, на мировом рынке постоянна, а предельные издержки производства возрастают, поэтому в оптимуме будет $MR_h = MR_f = MC$. При субсидировании внутренний спрос становится равным $q_d = 25+s-5$, тогда $MR_h = 35+s-2q$. Предельная выручка на конкурентном внешнем рынке равна мировой цене за вычетом экспортного налога, т.е. $MR_f = p_w-t = 60-t$. Наконец, $MC = 2q$, где $q = q_h+q_f$. Таким образом, оптимум фирмы описывается равенством $35+s-2q_h = 60-t = 2(q_h+q+f)$. Фактически это система двух уравнений с двумя неизвестными ($q_h$ и $q_f$) и двумя параметрами ($s$ и $t$). Решив систему относительно выпусков, получим $q_h = \frac{s+t-25}{2}$, $q_f= \frac{85-s-2t}{2}$.
Естественно, это при $s+t-25 \geqslant0$ и $85-s-2t\geqslant0$ – выпуск продукции не может быть отрицательным (случаи, когда один из выпусков равен нулю, тоже нет смысла рассматривать в этой задаче). Всё это можно было получить и без знания о предельных издержках и предельной выручке, а просто рассматривая квадратичную функцию прибыли от двух аргументов. Теперь можно записать, как от ставок субсидии и налога зависят расходы на субсидирование и доходы от налогообложения: $S = q_h s = s \frac{s+t-25}{2} \leqslant T = q_f t = t\frac{85-s-2t}{2}$.
Это неравенство можно привести к виду $25s+85t -s^2-2st-2t^2 \geqslant 0$.
Это будет «бюджетное ограничение» государства. Задача государства – максимизировать количество продаж на внутреннем рынке: $$q_h = \frac{s+t-25}{2} \rightarrow \max_{s, t}$$
Это равносильно максимизации суммы $s+t$; эту величину можно назвать $u=s+t$. Преобразуем бюджетное ограничение: $25u+60t-u^2-t^2 \geqslant 0$.
Таким образом, надо относительно $u$ решить квадратное неравенство $u^2 - 25u +(t^2-60t) \leqslant 0$, но не просто решить, а так, чтобы во множество решений вошло как можно большее значение $u$. Это означает, что неравенство будет выполнено как равенство и что искомое $u$ – это правый корень квадратного уравнения $u^2-25u+(t^2-60t) = 0$. Видим, что при $u^2$ и при $u$ стоят уже известные коэффициенты, а $t$ влияет только на параллельный сдвиг графика вверх-вниз, поэтому чтобы правый корень был как можно больше, надо сдвинуть график – параболу с ветвями вверх – как можно ниже, а для этого, очевидно, минимизировать $t^2-60t$.
Минимум достигается в $t=30$. Далее можно различным путями найти ставку субсидии. Например, подставить $t=30$, получить уравнение $u^2-25u -900 = 0$ и увидеть, что интересующий нас корень составляет $u=45$, откуда $s=15$. Значит, $q_h = 10$, $q_f = 5$, при этом $S=T = 150$. Достигнутый внутренний выпуск $q_h$ больше, чем можно было бы добиться простым запретом торговать на мировом рынке: в таком случае фирма внутри страны продавала бы $q_h = 8.75 < 10$. -
Если налог вводится по ставке не выше чем $t=25$, то фирма по-прежнему будет работать только на внешнем рынке, как и в отсутствие государственного вмешательства. Оптимум фирмы будет определяться равенством мировой цены за вычетом налога и предельных издержек: $60-t = 2q_f$, откуда $q_f = \frac{60-t}{2}$, $T = tq_f = t\frac{60-t}{2}$.
Если налог вводится по ставке выше $t = 25$, то фирма будет работать уже на обоих рынках, как в пункте 1, только этот случай будет отличаться отсутствием субсидии. Оптимум фирмы будет определяться равенством внутренней предельной выручки, мировой цены за вычетом налога и предельных издержек. Таким образом, можно просто в выкладки пункта 1 подставить $s=0$ и получить $q_f = \frac{85-2t}{2}$, $T = tq_f = t\frac{85-2t}{2}$.
Это будет продолжаться до тех пор, пока мировая цена минус налог не опустится ниже значения внутренней предельной выручки, которую в оптимуме получала бы фирма, если бы совсем не торговала на мировом рынке: $MR_h(8.75) = 17.5$. Таким образом, фирма будет торговать на двух рынках, если $60-t \geqslant 17.5$, или $t\leqslant 42.5$. При дальнейшем повышении ставки налога фирма перестаёт работать на мировом рынке: $q_f = 0$, $T=0$.
Итак,
$T = 0.5t(60-t)$ при $0\leqslant t \leqslant 25$
$T = 0.5t(85-2t)$ при $25\leqslant t \leqslant 42.5$
$T = 0$ при $ t \geqslant 42.5$.
Таким образом, вершина первой параболы с ветвями вниз находится правее границы, а вершина второй параболы с ветвями вниз находится левее границы. Это значит, что максимум будет достигаться в точности на границе промежутков при $t=25$.