Идея о том, что развитый финансовый сектор положительно влияет на экономический рост в стране, довольно давно присутствует в работах российских и зарубежных авторов.

1. Один из возможных механизмов положительного воздействия финансового сектора на будущий экономический рост носит название "канал фильтрации". Объясните, что "фильтруют" финансовые организации и почему это оказывает положительный эффект на экономический рост в последующие годы.
2. В дополнение к Пункту 1, назовите два (2) фактора, позволяющие объяснить положительный эффект, который развитый финансовый сектор оказывает на экономический рост, и опишите механизм их воздействия. Если вы укажете три фактора и более, то засчитаны будут только первые два.
3. Ряд исследований говорит о том, что избыточно развитый финансовый рынок может, наоборот, стать причиной для снижения темпов экономического роста. Как бы вы объяснили наличие подобного эффекта? Аргументируйте свой ответ.

В городе N, где раньше не было сотовой связи, появился оператор-монополист, предлагающий жителям два типа услуг. Первая услуга включает в себя 300 минут бесплатных звонков в месяц. Вторая услуга состоит из 10 ГБ бесплатного интернета в месяц. В городе живут две группы потребителей, одинаковые по численности, но разные по своим предпочтениям. Монополист выбирает цену, и если она оказывается приемлемой для покупателя, то он приобретает товар. В таблице, приведенной ниже, указана максимальная цена, которую каждая группа потребителей готова заплатить за конкретный продукт:

	300 минут  бесплатных звонков	10 ГБ бесплатного интернета
Потребители 1 группы	9 д.е.	x д.е.
Потребители 2 группы	6 д.е.	12 д.е.

Монополист может продавать услуги по отдельности, а может объединять их в пакет. При этом максимальная цена, которую покупатели готовы заплатить за пакет, определяется как сумма максимальных цен двух входящих в него услуг для каждой конкретной группы покупателей. Найдите, при каких значениях $x$ монополисту будет строго выгодно продавать пакет услуг (т.е. его прибыль в данном случае будет строго больше), и поясните полученные результаты.

В Далёкой-Далёкой Стране живут драконы. Они начинают работать в 20 лет и выходят на пенсию в 50 лет. Драконьи учёные провели большой опрос и установили, что зарплата драконов определяется по следующей формуле:

$$ w_{i}=20+3\cdot\left(age_{i}-20\right)-5\cdot gender_{i}+0,5\cdot gender_{i}\cdot\left(age_{i}-20\right) $$

где:

• $w_{i}$ — годовая (драконы получают зарплату раз в год!) зарплата дракона $i$ (в овцах);
• $age_{i}$ — возраст дракона $i$;
• $gender_{i}$ — пол дракона $i$ (эта переменная равна 0 для драконов-самцов и 1 для драконов-самок).

Ответьте на следующие вопросы:

1. Считая, что драконы работают с одинаковой производительностью независимо от пола, можно ли утверждать, что на их рынке труда присутствует ценовая дискриминация по половому признаку?Аргументируйте свой ответ, используя такие индикаторы, как среднемесячная / среднегодовая заработная плата, которую получает дракон $i$ за весь период своей трудовой деятельности (т.е. с 20 до 50 лет).
2. Согласно законодательству Далёкой-Далёкой Страны, все виды отпуска, который берут драконы, являются неоплачиваемыми.Пункт 1, если известно, что драконихи уходят в отпуск и уезжают на море на 1 месяц в году, а драконы (самцы) каждый год улетают в экскурсионный тур по достопримечательностям соседних королевств длиной в 3 месяца?

Король Артур славится своим гостеприимством. В его замке стоят 2 круглых стола, за которыми рассаживаются рыцари, когда съезжаются на званый обед. Рыцари любят просторно расположиться за столом, но в то же время охотно присоединяются к компании. Если за столом не очень тесно, то рыцари предпочитают сидеть в компании других рыцарей, а не проводить время в одиночестве. С другой стороны, когда за столом собирается слишком много рыцарей, может быть предпочтительнее сесть отдельно. Удовольствие, получаемое каждым конкретным рыцарем от посещения званого обеда, зависит от числарыцарей, сидящих с ним за одним столом, следующим образом:
$$U\left(n\right)=n\cdot\left(13-n\right)$$
где $n$ — это общее число всех рыцарей за столом, включая его самого. Можно считать, что рыцари знают количество приглашенных на званый обед; они съезжаются в замок по-одному, но в процессе могут пересаживаться из-за одного стола за другой. Если рыцарь игнорирует приглашение короля Артура и не приходит на званый обед, он получает нулевое удовольствие от посещения данного мероприятия.

1. Как рассядутся 7 приглашенных рыцарей, если каждый из них стремится максимизировать собственное удовольствие от посещения званого обеда? Как изменится ваш ответ, если приглашенных рыцарей 13? А если их 20?
2. Король Артур заботится обо всех своих гостях. Его удовольствие от званого обеда определяется как суммарное удовольствие всех приглашенных рыцарей. Также известно, что рыцари рассядутся именно так, как их попросит король Артур. Как изменится ваш ответ, если приглашенных рыцарей 13? А если их 20?

Правительства двух малых открытых экономик заключили между собой соглашение, которое обязывает компании проводить все торговые операции между этими двумя странами только в национальной валюте (первой или второй страны). До заключения данного соглашения все сделки осуществлялись в долларах США.

1. Прокомментируйте, с какой целью правительства указанных стран могли отказаться от использования доллара США в качестве основной валюты для сделок. Приведите две (2) экономически обоснованные причины. Если вы укажете три причины и более, то засчитаны будут только первые две.
2. Предложите две (2)аргумента в пользу того, почему компании в этих странах прежде предпочитали использовать доллар США, а не национальные валюты для международных расчетов. Если вы укажете три аргумента и более, то засчитаны будут только первые два.
3. С какими издержками, связанными с переводом расчетов в национальные валюты, могут столкнуться компании двух указанных экономик в краткосрочном периоде? Поясните ваш ответ.

Власти страны N обеспокоены криминогенной обстановкой в регионах своего государства. Для детального изучения причин существующих проблем президент страны N обратился к двум уважаемым ученым, Кнутову и Пряникову. Исследователи проделали огромную работу по сбору и обработке данных и вывели следующую эмпирическую закономерность:
$$r_{i}=12+0,25\cdot n_{i}^{homeless}+\beta\cdot X_{i}$$

• $r_{i}$ отражает уровень преступности в регионе $i$, измеренный как общее количество преступлений, совершенных за год;
• $n_{i}^{homeless}$ определяет общее число бездомных в регионе $i$ за год;
• $\beta\cdot X_{i}$ улавливает влияние прочих региональных факторов на уровень преступности.

Кнутов и Пряников интерпретировали полученные результаты следующим образом:

"Согласно проведенному анализу, именно высокое количество бездомных в регионе провоцирует рост уровня преступности. В качестве основной рекомендации властям страны предлагается обеспечить бездомных жильем, что приведет к значительному снижению общего числа совершенных преступлений."

Поскольку Кнутов и Пряников являются уважаемыми экспертами, президент страны N последовал их совету и затратил значительную сумму бюджетных средств на обеспечение бездомных жильем, что позволило достичь $n_{i}^{homeless}=0$ в каждом из регионов. Однако указанные меры не привели к ожидаемому снижению уровня преступности: данный показатель практически не изменился!

1. Чем можно объяснить тот факт, что общий уровень преступности не снизился в результате предпринятых властями страны мер по обеспечению бездомных жильем, несмотря на аналитические выкладки Кнутова и Пряникова?
2. Несмотря на провал реформы, предложенной Кнутовым и Пряниковым, президент страны N все же намерен выяснить, является ли рост числа бездомных в регионе причиной увеличения общего уровня преступности. Один из стандартных подходов к выявлению причинно-следственных связей подразумевает деление выборки на контрольную и испытуемую группы случайным образом. Предполагается, что данные группы идентичны по всем характеристикам. Реформа, эффект которой нужно оценить, применяется только к испытуемой группе, тогда как для контрольной группы ничего не изменяется. Поскольку исходные условиях были идентичны для обеих групп, наблюдаемые различия объясняются исключительно реформой, которой подверглась испытуемая группа. Используя логику указанного метода, предложите "идеальный" подход (не обязательно реализуемый на практике) для выявления причинно-следственной связи между количеством бездомных в регионе и общим уровнем преступности посредством проведения реформы, направленной на обеспечение бездомных жильем. Укажите две (2) причины, по которым такой подход может быть сложно реализовать на практике. Если вы укажете три причины и более, то засчитаны будут только первые две.

Рыночный спрос на товар Х описывается функцией $q_{d}\left(p\right)=2-p$. В данный момент на рынке товара Х в качестве монополиста действует фирма $A$; фирма $B$ рассматривает возможность входа на этот рынок. Отличительная особенность функционирования данной отрасли состоит в том, что фирма $A$ обладает патентом на производство товара Х. Это значит, что если фирма $B$ захочет выпускать товар Х, то ей придётся перечислять фирме $A$ роялти — платёж в размере \$$t$ с каждой произведённой единицы продукции — за право пользоваться запатентованной технологией. Производство единицы товара Х с помощью этой технологии обходится в \$1. Взаимодействие фирм на рынке происходит следующим образом:

• Фирма $A$ выбирает свой объём выпуска $q_{A}$, величину роялти $t$ и объявляет их;
• После этого фирма $B$, зная выпуск фирмы $A$ и размер роялти, принимает своё решение об объеме производства $q_{B}$

Ответьте на следующие вопросы:

1. Какой размер роялти установит фирма $A$? Какими при этом будут объемы выпуска и прибыль обеих фирм?
2. Предположим, что у фирмы $B$ имеется административный ресурс, благодаря которому половину расходов, связанных с производством товара Х, ей компенсируют из бюджета. Иначе говоря, производство единицы товара Х с помощью технологии фирмы $A$ будет обходиться фирме $B$ дешевле: не в \$1, а в \$0,5. При этом расходы фирмы $B$ на выплату роялти в пользу фирмы $A$ не компенсируются. Структура издержек фирмы $A$ осталась неизменной: как и прежде, она затрачивает \$1 на производство единицы товара X. Как изменятся ваши ответы на вопросы Пункта 1 при новых условиях? Прокомментируйте полученные результаты.

В самом упрощенном виде деятельность коммерческих банков представляет собой привлечение депозитов вкладчиков, часть из которых направляется на формирование резервов банка, а часть (вместе с собственными средствами банка) выдается фирмам и домохозяйствам в форме кредитов. По статистике средний срок хранения депозита в банке составляет не более 5 лет, в то время как кредиты могут выдаваться и на более длительный период (так, средний срок ипотечного кредита в России составляет 14,9 лет). Помимо этого, банки, как правило, проводят депозитные и кредитные операции не только в национальной валюте страны, в которой они находятся, но и в некоторых иностранных валютах (например, российский банк может принимать депозиты и выдавать кредиты в долларах или евро). Процентные ставки по депозитам и кредитам при этом определяются банком в момент заключения договора с вкладчиком/заемщиком на основе множества параметров, таких как текущая ситуация на денежном рынке, соотношение активов и пассивов банка и его ожидания относительно макроэкономической ситуации в будущем.

1. С какими рисками, связанными с хранением депозитов и выдачей кредитов, может столкнуться банк? Каким образом они угрожают его финансовой стабильности?
2. На практике банки не всегда хорошо контролируют те риски, которые вы перечислили в Пункте 1, и зачастую недооценивают их значимость. Поскольку стабильность финансовой системы страны напрямую зависит от стабильности отдельных агентов, которые в нее входят, регуляторы часто используют специальные меры финансового регулирования, направленные на снижение банковских рисков. Предложите три (3) различные меры, которые будут направлены на уменьшение представленных вами в Пункте 1 рисков. Если вы предложите больше трех мер, засчитаны будут только первые три.
3. Перечислите общие недостатки всех мер регулирования, которые были предложены вами в Пункте 2.

Фирма-совершенный конкурент работает на рынке, где цена установилась на уровне $p$ д.е. Производство $q$ единиц продукции обходится фирме в $\frac{q^{2}}{100}$ д.е. По итогам независимого аудита выяснилось, что доля $x\in\left(0,\,1\right)$ от всей произведённой фирмой продукции пропадает со склада и не доходит до продажи. В связи с этим фирма приняла решение нанять инспекторов, которые должны контролировать, чтобы произведённая продукция не исчезала со склада. Известно, что во избежание пропажи $Y$ единиц продукции (независимо от совокупного выпуска $q$), фирме необходимо потратить $\frac{Y^{2}}{16}$ д.е.

Пример. Допустим, фирма производит $q=50$ единиц продукции, 40% которой ($x=0,4$) исчезает со склада. Тогда без дополнительных инспекций до рынка дойдет лишь $\left(1-x\right)\cdot q=30$ единиц продукции. Если фирма хочет реализовать 38 единиц продукции из 50, она должна предотвратить пропажу $Y=8$ единиц продукции, затратив при этом $\frac{Y^{2}}{16}=4$ д.е.

1. Определите, как объем производства фирмы $q$ зависит от доли пропавшей продукции $x$ и конкурентной цены $p$ при условии использования возможности мониторинга.
2. При каком значении $x$ количество фактически исчезнувшей со склада продукции (т.е. величина $\left(x\cdot q-Y\right)$ при использовании возможности мониторинга) будет максимальным?

В замке короля Артура есть 2 круглых стола, за которыми рассаживаются рыцари, когда съезжаются на званый обед. Рыцари любят просторно расположиться за столом, но также ценят и дружеское общение. Поэтому если за столом не очень тесно, они предпочтут сидеть в компании других рыцарей, чем оставаться в одиночестве. С другой стороны, если слишком много рыцарей располагаются за одним столом, может быть предпочтительнее переместиться за другой стол. Общее удовольствие, получаемое каждым конкретным рыцарем от посещения званого обеда, зависит от числа рыцарей, сидящих с ним за одним столом, следующим образом:
$$
U\left(n\right)=n\cdot\left(13-n\right)
$$
где $n$ — это число всех рыцарей, расположившихсяза конкретным столом, включая его самого. В свою очередь король Артур как радушный хозяин заботится о том, чтобы суммарное удовольствие всех его гостей было максимальным, и в случае, когда король Артур рассаживает рыцарей самостоятельно, он максимизирует именно эту величину. Можно считать, что рыцари знают количество приглашенных на званый обед; они съезжаются в замок по-одному, но в процессе могут пересаживаться из-за одного стола за другой. Если рыцарь игнорирует приглашение короля Артура и не приходит на званый обед, он получает нулевое удовольствие от посещения данного мероприятия.
Распределение рыцарей по столам считается устойчивым, если ни у одного рыцаря (или группы рыцарей) нет стимула его нарушить.При каком количестве рыцарей распределение их по столам будет устойчивым и одинаковым вне зависимости от того, рассаживались ли они сами или же их распределил по столам король Артур?

В замке короля Артура есть 1 круглый стол, за которым рассаживаются рыцари, когда съезжаются на званый обед. Рыцари любят просторно расположиться за столом, но также не отказываются от общения в компании. Поэтому удовольствие, которое получает каждый рыцарь от посещения званого обеда, зависит от числа рыцарей, что сидят за столом, следующим образом:
$$ U\left(n\right)=n\cdot\left(13-n\right)$$
где $n$ — это общее число всех рыцарей за столом, включая его самого. Рыцари съезжаются на обед, только если получают положительное удовольствие от его посещения. В свою очередь король Артур заботится обо всех своих гостях, и его удовольствие от званого обеда равно сумме удовольствий приглашенных рыцарей.

1. Какое максимальное число рыцарей можно видеть за столом короля Артура?
2. Какое количество приглашенных оптимально с точки зрения каждого рыцаря, который желает получить максимальное удовольствие от посещения званого обеда?
3. Какое количество приглашенных оптимально с точки зрения короля Артура, который желает, чтобы суммарное удовольствие всех присутствующих на обеде было максимально?
4. Сравните количество приглашенных рыцарей в Пунктах 2 и 3 и объясните, почему можно было бы предугадать результат этого сравнения, не проводя расчетов.

Вместе с повышением пенсионного возраста правительство Российской Федерации разработало ряд мер для защиты работников предпенсионного возраста. К данной категории относятся работники, которым до наступления пенсионного возраста осталось не более 5 лет. Одна из таких мер предусматривает наложение штрафа на предприятие в размере до 200 тыс. руб. за необоснованное увольнение работника предпенсионного возраста.

1. Приведите два (2) аргумента, объясняющих, почему введение санкций за увольнение работников предпенсионного возраста может негативно сказаться на прибыли российских компаний, которые не нарушают закони, соответственно, не платят штраф, упомянутый выше. Если вы укажете три аргумента и более, то засчитаны будут только первые два.
2. Предложите три (3) различных и не противоречащих вступающему в силу закону (т.е. фирма не увольняет работников предпенсионного возраста) варианта того, как компании могут начать действовать в обход указанных в задании санкций. Если вы приведете четыре варианта и более, то засчитаны будут только первые три.

В некотором регионе есть три города: $A$, $B$ и $C$ — попарно соединенных дорогами.
Стоимость отправки посылки весом $w$ кг. между двумя городами определяется следующим образом:

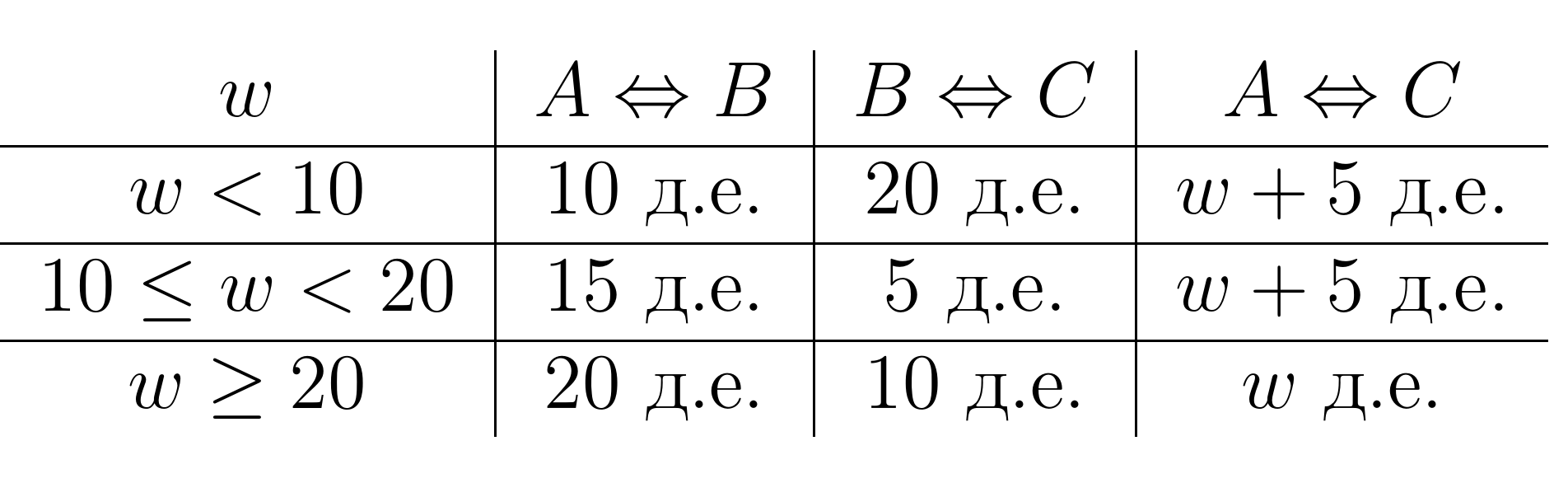
Бабушка Агриппина, живущая в городе $A$, хочет отправить подарки двум своим внукам: Васе и Соне. Вася живет в городе $B$, а Соня — в городе $C$. Бабушка может отправить посылку как напрямую в нужный город, так и через другой город, и при этом она всегда выбирает самый дешевый способ пересылки. Так, например, бабушка может отправить подарок весом $w=15$ кг. в город $B$ напрямую, заплатив 15 д.е., или же через город $C$, отдав $\left(15+5\right)+5=25$ д.е. Если два способа пересылки стоят одинаково, бабушка Агриппина всегда предпочитает отправлять подарок напрямую.

1. Определите, какую сумму бабушка Агриппина затратит на пересылку подарка каждому из внуков в зависимости от веса его посылки $w$ кг., если она действует оптимально. Ответ представьте, заполнив таблицу, приведенную ниже, и поясните своё решение (обратите внимание, что в одной категории веса (например, $10\leq w<20$) возможны различные варианты пересылки отправления).
   
2. Бабушка любит обоих внуков одинаково и поэтому отправляет им посылки одного и того же веса $w$ кг. Представьте график суммарных затрат бабушки Агриппины на отправку обеих посылок Васе и Соне, где ось X соответствует весу одного подарка $w$ кг., а ось Y — суммарной стоимости пересылки обоих подарков $p$ д.е. Поясните ваши расчеты.
3. Известно, что бабушка Агриппина потратила в сумме 45 д.е. на пересылку подарков обоим внукам. Определите, сколько весил подарок каждому из внуков и сколько бабушка Агриппина потратила на пересылку каждого из них.

С целью сокращения потребления сладких газированных напитков правительство страны N предложило установить минимальную цену $p$ денежных единиц (д.е.) за литр газировки. При этом уровень цены $p$ д.е. оказался выше, чем цена одного литра большинства газированных напитков, представленных в стране N. На рынке газированных напитков страны N присутствуют 4 крупных производителя, каждый из которых контролирует примерно 15% рынка и входит в Ассоциацию производителей безалкогольных напитков (АПБН), и множество мелких региональных производителей, доля каждого из которых не превышает 1% рынка. АПБН поддержала предложение правительства ввести минимальную цену $p$ д.е. за литр газированного напитка.

1. Как вы думаете, чем может быть обосновано решение АПБН поддержать инициативу правительства о введении минимальной цены $p$ д.е. за литр, ведь повышение цены при прочих равных условиях приведет к сокращению потребления газированных напитков и падению объема продаж?
2. На ваш взгляд, какой могла быть стратегия большинства мелких региональных производителей газированных напитков до введения минимальной цены $p$ д.е. за литр (иначе говоря, в чем было их преимущество перед крупными компаниями)? Какую стратегию вы бы посоветовали им использовать после введения минимальной цены за литр газировки?
3. Оппозиционная партия выступила с резкой критикой введения минимальной цены на газированные напитки как направленной против бедных слоев граждан. В частности, лидер оппозиционной партии заявил, что повышение цены газированных напитков сильнее всего затронет самые незащищенные слои населения, поскольку для них доля расходов на газировку в совокупных доходах составляет около 7%. Тогда если в результате введенных мер средняя цена за литр газировки увеличится в $x>0$ раз, то на данную статью расходов будет приходиться около $x\cdot$7% совокупных доходов наименее обеспеченных домашних хозяйств, что заставит их начать экономить на остальных товарах. В то же время более богатые домашние хозяйства, для которых доля расходов на газированные напитки в совокупных доходах составляет менее 1%, не ощутят повышения цены данного блага. Согласны ли вы с аргументами лидера оппозиционной партии? Обоснуйте свой ответ.

Вместе с повышением пенсионного возраста правительство Российской Федерации разработало ряд мер для защиты работников предпенсионного возраста. К данной категории относятся работники, которым до наступления пенсионного возраста осталось не более 5 лет. Одна из таких мер предусматривает наложение штрафа на предприятие в размере до 200 тыс. руб. за необоснованное увольнение работника предпенсионного возраста.

1. Приведите два (2) аргумента, объясняющих, почему введение санкций за увольнение работников предпенсионного возраста может негативно сказаться на прибыли российских компаний, которые не нарушают закони, соответственно, не платят штраф, упомянутый выше. Если вы укажете три аргумента и более, то засчитаны будут только первые два.
2. Предложите три (3) различных и не противоречащих вступающему в силу закону (т.е. фирма не увольняет работников предпенсионного возраста) варианта того, как компании могут начать действовать в обход указанных в задании санкций. Если вы приведете четыре варианта и более, то засчитаны будут только первые три.

Король Артур славится своим гостеприимством. В его замке стоят 2 круглых стола, за которыми рассаживаются рыцари, когда съезжаются на званый обед. Рыцари любят просторно расположиться за столом, но в то же время охотно присоединяются к компании. Если за столом не очень тесно, то рыцари предпочитают сидеть в компании других рыцарей, а не проводить время в одиночестве. С другой стороны, когда за столом собирается слишком много рыцарей, может быть предпочтительнее сесть отдельно. Удовольствие, получаемое каждым конкретным рыцарем от посещения званого обеда, зависит от числарыцарей, сидящих с ним за одним столом, следующим образом:
$$U\left(n\right)=n\cdot\left(13-n\right)$$
где $n$ — это общее число всех рыцарей за столом, включая его самого. Можно считать, что рыцари знают количество приглашенных на званый обед; они съезжаются в замок по-одному, но в процессе могут пересаживаться из-за одного стола за другой. Если рыцарь игнорирует приглашение короля Артура и не приходит на званый обед, он получает нулевое удовольствие от посещения данного мероприятия.

1. Как рассядутся 7 приглашенных рыцарей, если каждый из них стремится максимизировать собственное удовольствие от посещения званого обеда? Как изменится ваш ответ, если приглашенных рыцарей 13? А если их 20?
2. Король Артур заботится обо всех своих гостях. Его удовольствие от званого обеда определяется как суммарное удовольствие всех приглашенных рыцарей. Также известно, что рыцари рассядутся именно так, как их попросит король Артур. Как изменится ваш ответ, если приглашенных рыцарей 13? А если их 20?

Не секрет, что доходы человека зависят от уровня его образования, обладания уникальными навыками, от должности, которую он занимает. Тогда логично предположить, что заработные платы людей со схожей квалификацией — скажем, педагогов дошкольных учебных заведений — должны быть более-менее сопоставимыми на региональном уровне. Однако по данным официальной статистики в период с января по сентябрь 2016г. средняя заработная плата такого работника в Московской области составляла 42 521 руб., в Ленинградской области — 34 352 руб., в Ростовской области — 18 152 руб., в Республике Дагестан — 14 605 руб., в Нижегородской области — 25 008 руб., в Тюменской области — 47 205 руб.

1. Приведите два (2) различных рыночных фактора, которые могут объяснить существующий разрыв в уровне заработных плат работников со схожей квалификацией на межрегиональном уровне. Если вы укажете три фактора и более, то засчитаны будут только первые два.
2. Может ли рабочий средней квалификации (скажем, электрик) получать заработную плату больше, чем специалист с высшим образованием, находящийся в том же регионе? Аргументируйте свой ответ: если он отрицательный, поясните почему; если положительный, дополнительно укажите, при каких условиях будет наблюдаться подобная ситуация.

В одном городе есть хоккейный клуб, для стабильного существования которого требуется компания, готовая стать его генеральным спонсором. Губернатор озадачился поиском финансирования для клуба, представляющего город в хоккейной лиге. Он обратился к фирме-монополисту, которая производит единицу продукции с издержками 2 д.е. и реализует товар на рынке, где спрос описывается функцией $q_{d}\left(p\right)=12-p$. Также фирма-монополист уплачивает потоварный налог по ставке 4 д.е. Губернатор не может направить эти налоговые поступления на финансирование хоккейного клуба, а взимание аккордных налогов запрещено законом. Чтобы заинтересовать фирму-монополиста в спонсорской деятельности, губернатором была предложена следующая схема:

• Фирма-монополист может выбрать сумму $x$ д.е. и внести её в пользу хоккейного клуба;
• В обмен на спонсорскую поддержку хоккейного клуба губернатор готов снизить ставку потоварного налога для фирмы-монополиста до величины $\left(4-\beta\cdot x\right)$ д.е. при $\left(4-\beta\cdot x\right)\geq0$ или до нуля, если $\left(4-\beta\cdot x\right)$ принимает отрицательные значения.

Считайте, что если фирме-монополисту безразлично, платить потоварный налог по базовой ставке 4 д.е. или же спонсировать хоккейный клуб, то она всегда предпочитает второй вариант (т.е. поддержку спорта). Величина налоговых льгот (коэффициент $\beta$) выбирается губернатором.

1. Найдите все значения $\beta$, при которых фирма-монополист согласится стать спонсором хоккейного клуба.
2. Какую величину налоговых льгот $\beta$ должен выбрать губернатор, если он хочет, чтобы размер спонсорской помощи хоккейному клубу $x$ д.е. был максимальным? Сколько при этом составит бюджет хоккейного клуба, т.е. величина $x_{\text{max}}$ д.е.?
3. Допустим, губернатор установил величину налоговых льгот $\beta$ на уровне, который вы определили в Пункте 2. Сравните налоговые отчисления фирмы при отказе от поддержки хоккейного клуба (т.е. при $x=0$) и размер спонсорской помощи $x_{max}$ д.е. Будет ли найденное вами соотношение между двумя указанными величинами (знак неравенства) оставаться таким же при других функциях спроса и иных издержках производства единицы продукции для фирмы-монополиста? Используйте формальные выкладки для аргументации своего ответа.