10 класс

1. Монополист Везучий

Монополист Н. Е. Везучий оказался в затруднительном положении: в краткосрочном периоде в оптимуме оказалось, что выручка покрывает только переменные издержки. Спрос на рынке описывается функцией $P=150-3Q$, в оптимуме монополист продаёт 10 единиц продукции, отсутствует возможность ценовой дискриминации. Найдите вид функции переменных издержек, если известно, что функция средних переменных издержек AVC описывается параболой, минимум которой достигается при Q=12.
Решение

Найдём равновесие, если Q=10, P=120.
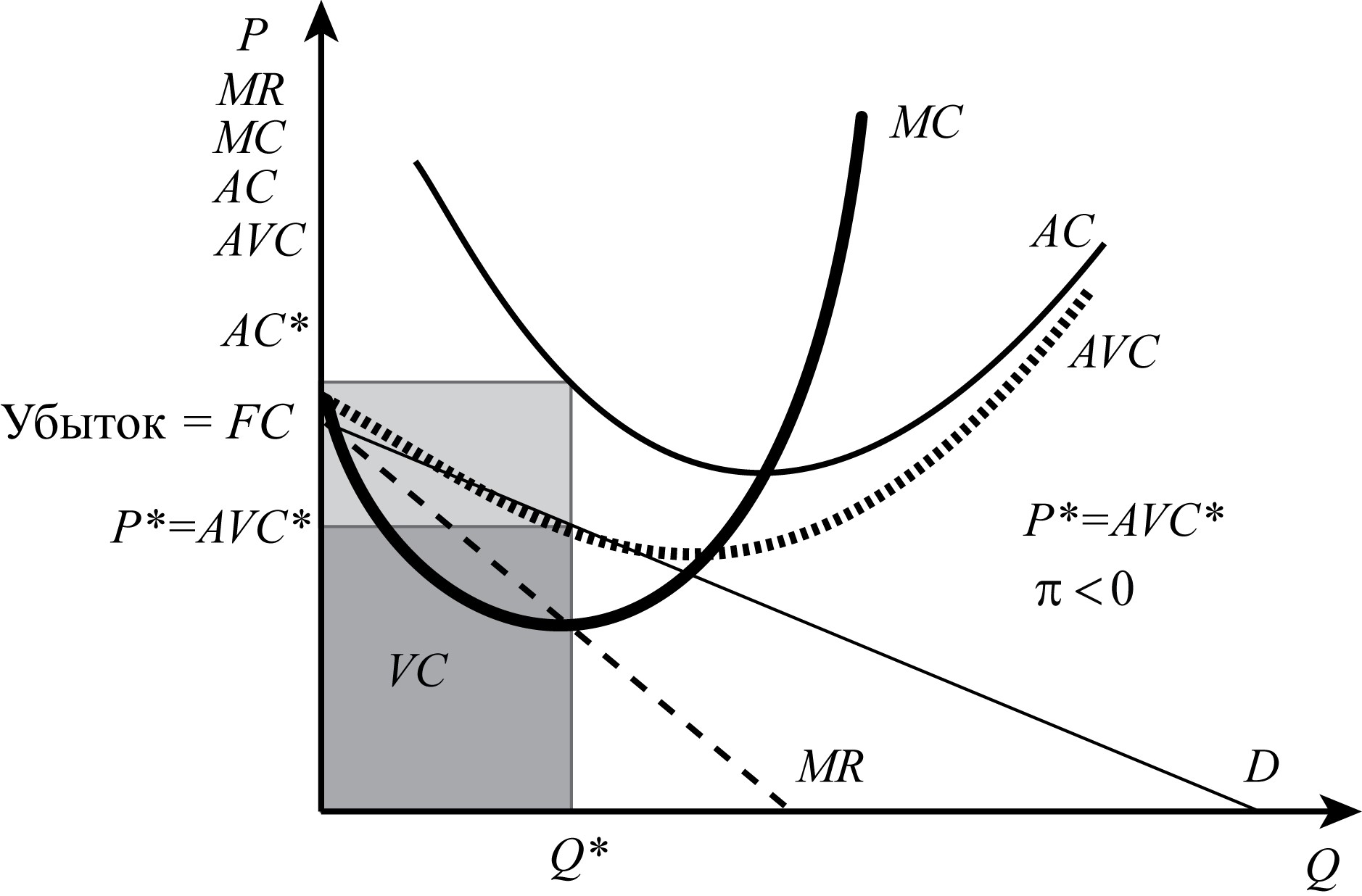
Восстановим функцию переменных издержек VC. Не важно, уходить с рынка или нет, значит прибыль =-FC. Если в оптимуме прибыль =-FC, то ситуация выглядит так:

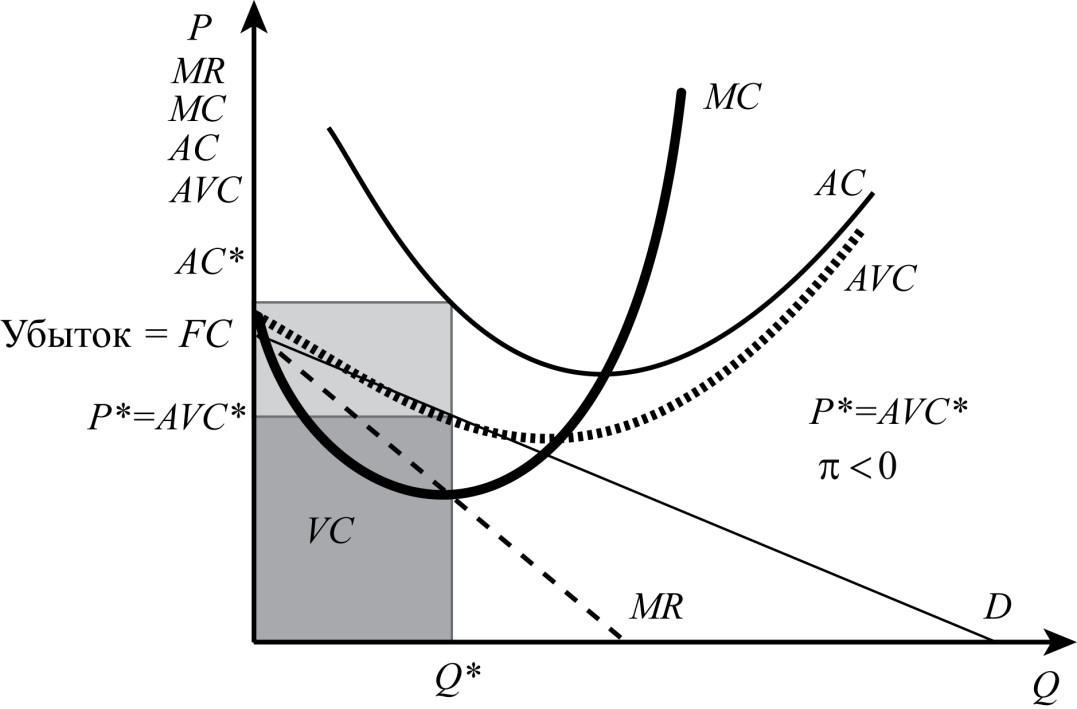
В этом случае должны выполняться условия:

  1. спрос касается AVC при Q=10
  2. AVC=P при Q=10.

    Пункты 1 и 2 верны, так как в точке оптимума прибыль:

    $$\pi=P\cdot Q^*-AVC\cdot Q^*-FC=Q^*\cdot(P-AVC)-FC$$

  3. MC=MR при Q=10, так как это точка оптимума.

Введём функцию $AVC=aQ^2+bQ+c$. Подставим всю известную информацию:

  1. $AVC'_Q=P'_Q \Rightarrow 2aQ+b=-3 \Rightarrow 20a+b=-3 \Rightarrow b=-3-20a$
  2. $aQ^2+bQ+c=120 \Rightarrow 100a+10b+c=120 \Rightarrow c=120-100a-10\cdot(-3-20a) \Rightarrow c=150+100a$
  3. $Q_b=-\dfrac{b}{2a}=12 \Rightarrow b=-24a=-3-20a \Rightarrow a=\dfrac{3}{4} \; b=-18$

    $c=150+100a=225 \Rightarrow VC=0{,}75Q^3-18Q^2+225Q$

Разбалловка: всего нужно найти 3 коэффициента, при $Q^3$, при $Q^2$ и при $Q$.
За первый верно найденный коэффициент ставится 4 балла, за второй – 4 балла, за третий – 3 балла.

2. Автозаправка

На рынке автозаправок действует компания-монополист, заправка которой расположена на расстоянии s от поставщика бензина. Поставщик продаёт бензин компании-монополисту по цене 30 у.е. за литр. Известно, что для того, чтобы доставить Q литров на расстояние s, компания-монополист затрачивает 0,5sQ литров бензина на заправку бензовоза. Других издержек компания-монополист не несёт. Спрос на бензин на заправке не зависит от её расположения и составляет $Q^d=120-P^d$. Государство облагает налогом компанию за каждый закупленный у поставщика литр бензина (независимо от того, продают ли его на заправке или используют для транспортировки) по ставке, которая максимизирует поступления в бюджет. Определите, на каком расстоянии от поставщика компания расположила заправку, если известно, что цена бензина на ней составила 105 у.е.
Решение

Суммарные издержки компании-монополиста (3 балла): $$TC(Q)=(30+t)(Q+0{,}5sQ)=(30+t)(1+0{,}5s)\cdot Q \Rightarrow MC=(30+t)(1+0{,}5s)$$
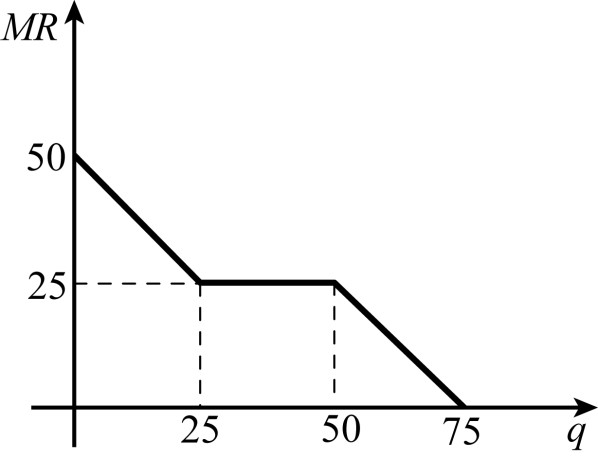
Суммарная выручка: $$TR(Q)=120Q-Q^2 \Rightarrow MR=120-2Q$$
Оптимум монополиста достигается при равенстве предельных издержек и выручки: $$120-2Q=(30+t)(1+0{,}5s) \Rightarrow Q=60-0{,}25(30+t)(s+2) \Rightarrow P=60+0{,}25(30+t)(s+2) \; \textbf{ (2 балла)}$$
Государство максимизирует поступления в бюджет (с учётом того, что налогом облагается каждый закупленный у поставщика литр бензина (независимо от того, продают ли его на заправке или используют для транспортировки):
$$\begin{equation} T=t\cdot Q\cdot (1+0{,}5s)=t\cdot\bigl(60-0{,}25(30+t)(s+2)\bigr)\cdot(1+0{,}5s) \\
t^*=\dfrac{60-7{,}5(2+s)}{0{,}5(2+s)}=\dfrac{120-15(s+2)}{2+s}=\dfrac{120}{s+2}-15 \; \textbf{ (3 балла)} \\
P=60+0{,}25\left(30+\dfrac{120}{s+2}-15\right)(s+2)=60+0{,}25\bigl(120+15(s+2)\bigr)=90+\dfrac{15}{4}(2+s) \\
P=105 \Rightarrow s=2 \textbf{ (3 балла)} \end{equation}$$

3. Геймеры и новички

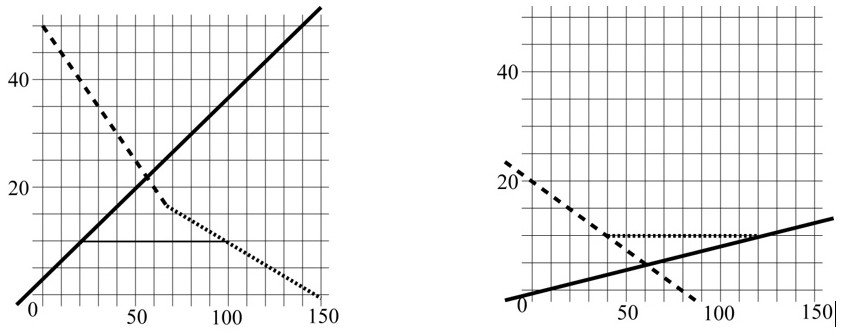
На рынке компьютерных игр есть две категории покупателей – геймеры и новички. Спрос геймеров задаётся функцией $Q=50-\dfrac{1}{3}P$, а спрос новичков задаётся функцией $Q=50-\dfrac{1}{3}P$. Предложение на рынке компьютерных игр имеет вид $Q=-10+P$.

Пусть государство вводит потоварный налог на производителей в размере t за единицу продукции. Известно, что равновесное количество сократилось на 30 единиц. Чему равна ставка налога t?

Решение

Составим общую функцию спроса. При цене выше 150 рублей никто не покупает игры, при цене в интервале от 75 до 150 рублей игры покупают только геймеры. При цене ниже 75 рублей игры покупают обе категории потребителей. Таким образом, общая функция спроса:

$\begin{cases} 0, & P>150 \\ 50-\dfrac{1}{3}P, & 75\lt P\leq150 \;\;\;\;\;\textbf{(4 балла)} \\ 100-P, & P\leq75 \end{cases}$

Далее находим равновесную цену и количество. Функция $Q=-10+P$ пересекает функцию спроса на третьем участке в точке Q=45, P=55 (2 балла).

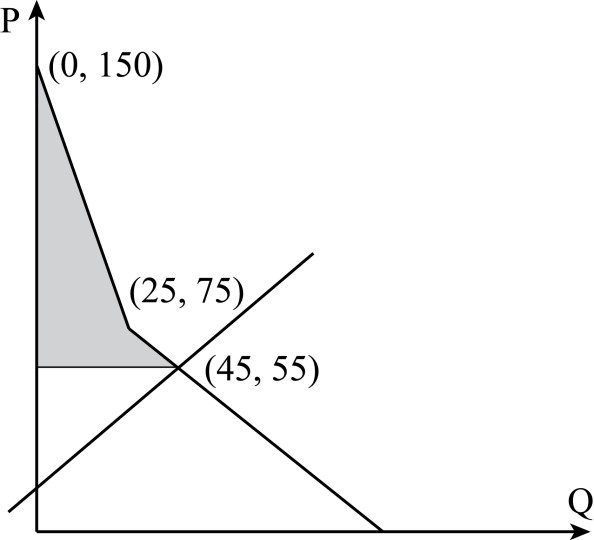
Новое равновесное количество уменьшилось на 30 единиц и стало равно 15. Тогда равновесная цена равна 105, покупают игры только геймеры (2 балла).
Новая функция предложения: $Q=-10+P-t$. Подставляя равновесные цену и количество, получаем, что ставка налога равна 80 (3 балла).

4. Фермер Хоггет

Артур Хоггет занимается разведением животных. На его ферме каждое лето могут жить до 100 уток или до 20-ти поросят. Утки и поросята могут соседствовать на одной ферме в любом линейном соотношении. Хоггет может обмениваться животными с соседом в такой пропорции, что за каждые 20 уток можно получить 3-х поросят и наоборот, причём у соседа есть 100 уток и 50 поросят. Ежегодно Артура Хоггета приглашают на ярмарку в город, где ему готовы заплатить 5\$ за каждую утку и 30\$ за каждого поросёнка. Сколько максимально сможет заработать Артур Хоггет по итогам одного лета?
Решение

Пропорция обмена выгодна Хоггету, он может увеличить свои производственные возможности. Пусть Хоггет произвёл 20 поросят: 15 можно обменять на 100 уток, а оставшиеся 5 поросят эквивалентны 25 уткам.
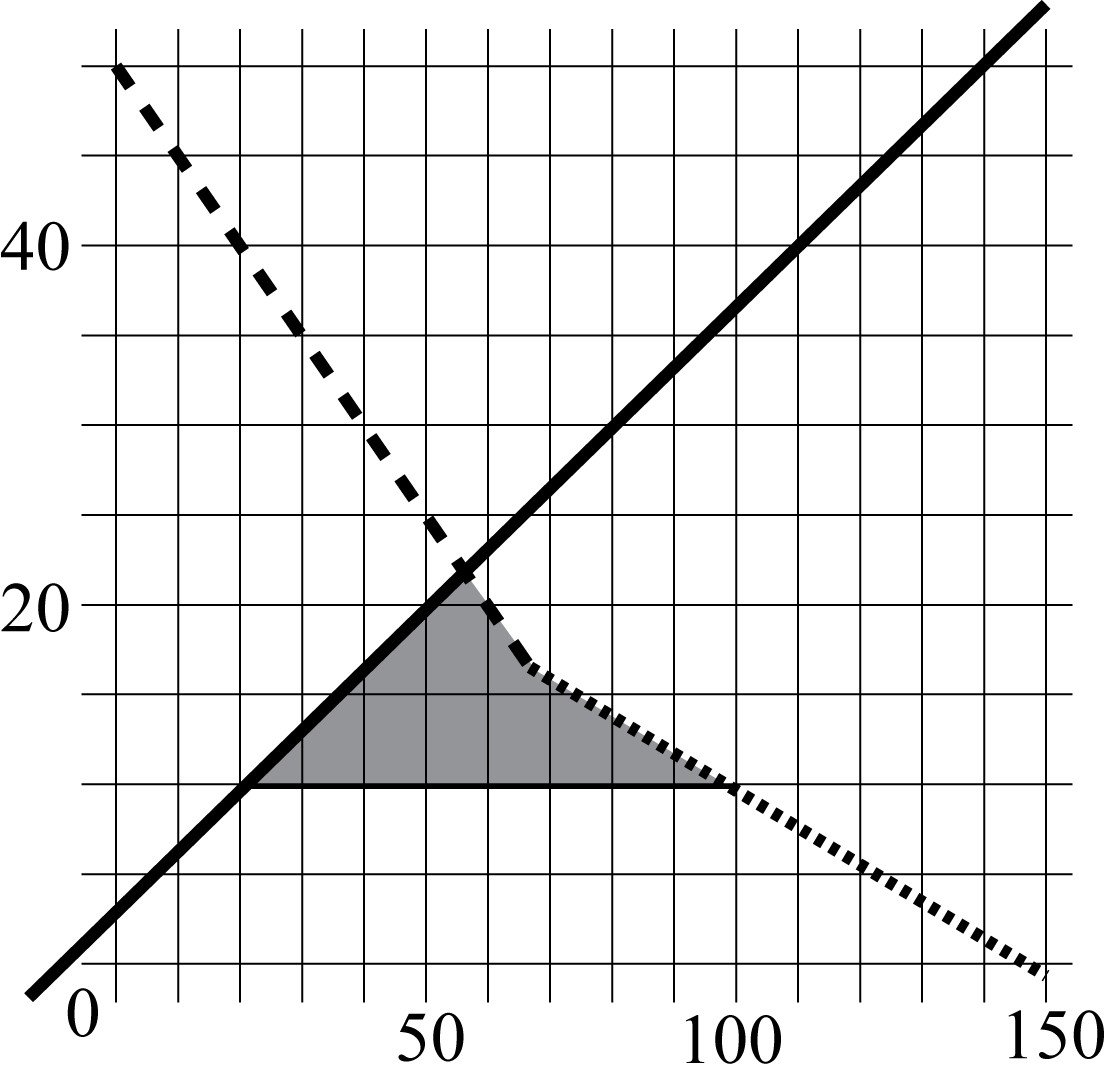
Кривая торговых возможностей Хоггета при обмене с соседом выглядит так (6 баллов):

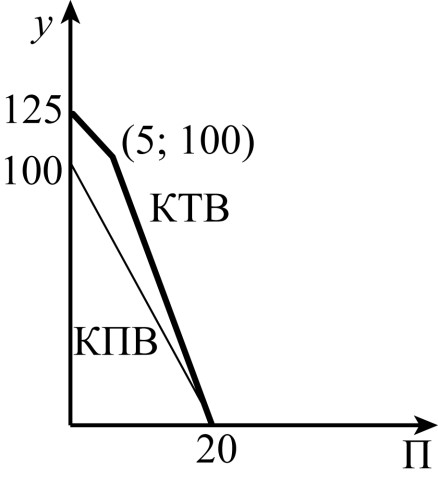
Исходя из цен, которые предлагают на ярмарке, Хоггету необходимо продать поросят и уток в пропорции 1:6. Проведём линии уровня с такой пропорцией:

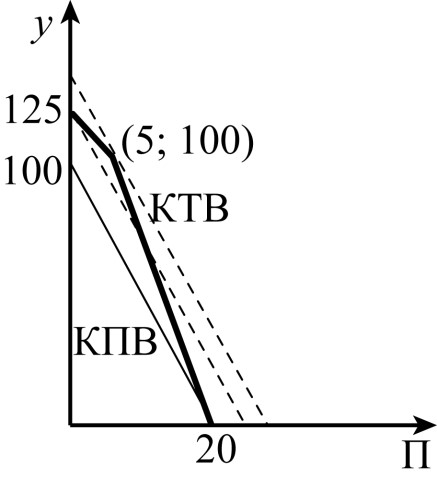
Самая дальняя от начала координат линия уровня пересекает КТВ в точке (5;100). Таким образом, максимально возможный доход $=5\cdot30+100\cdot5=650$.
Также можно рассуждать иначе. Пусть Хоггет производит только уток, тогда 1 поросенок стоит 30\$ и эквивалентен 5-ти уткам, которые стоят 25\$ – имеет смысл переключаться на производство поросят. Мы переходим на графике в точку (5;100). Теперь 1 дополнительный поросёнок за 30\$ эквивалентен 20/3 уток, которые стоят $\dfrac{20}{3}\cdot5>30$, то есть невыгодно дальше производить поросят (5 баллов за любой способ рассуждения).

11 класс

1. Монополист Везучий-2

Монополист Н. Е. Везучий оказался в затруднительном положении: в краткосрочном периоде в оптимуме оказалось, что выручка покрывает только переменные издержки. Спрос на рынке описывается функцией $P=150-3Q$, в оптимуме монополист продаёт 10 единиц продукции, отсутствует возможность ценовой дискриминации. Известно, что функция средних переменных издержек AVC описывается параболой, минимум которой достигается при Q=12.

Пусть государство, считая производство монополиста очень важным для страны, вводит потоварную субсидию монополисту в размере 375 ден. ед. на одну единицу продукции. Найдите новое оптимальное количество.

Решение

Найдём равновесие, если Q=10, P=120.
Восстановим функцию переменных издержек VC. Не важно, уходить с рынка или нет, значит прибыль равна -FC. Если в оптимуме прибыль равна -FC, то ситуация выглядит так:

В этом случае должны выполняться условия:

  1. спрос касается AVC при Q=10
  2. AVC=P при Q=10.

    Пункты 1 и 2 верны, так как в точке оптимума прибыль:

    $$\pi=P\cdot Q^*-AVC\cdot Q^*-FC=Q^*\cdot(P-AVC)-FC$$

  3. MC=MR при Q=10, так как это точка оптимума.

Введём функцию $AVC=aQ^2+bQ+c$. Подставим всю известную информацию:

  1. $AVC'_Q=P'_Q \Rightarrow 2aQ+b=-3 \Rightarrow 20a+b=-3 \Rightarrow b=-3-20a$
  2. $aQ^2+bQ+c=120 \Rightarrow 100a+10b+c=120 \Rightarrow c=120-100a-10\cdot(-3-20a) \Rightarrow c=150+100a$
  3. $Q_b=-\dfrac{b}{2a}=12 \Rightarrow b=-24a=-3-20a \Rightarrow a=\dfrac{3}{4} \; b=-18$

    $c=150+100a=225 \Rightarrow VC=0{,}75Q^3-18Q^2+225Q$

Если введена субсидия в размере 375 единиц, то новая функция $VC=0{,}75Q^3-18Q^2+225Q-375Q$ (7 баллов)

Тогда: $MC=\dfrac{9}{4}Q^2-36Q-150=150-6Q=MR$

Новое $Q^*=20$ (4 балла).

2. Хлеб всему голова

Фирма «Хлеб всему голова» закупает на рынке муку и поставляет на рынок хлеб. Текущая цена хлеба на рынке 20, объём производства составляет 10 батонов в день и является неизменным, текущая цена муки на рынке 5, и на каждую единицу хлеба требуется 2 единицы муки. Других издержек фирма не несёт. Владелец фирмы ожидал завтра рост цены на рынке хлеба на 40 процентов и рост закупочной цены на рынке муки в 2 раза, поэтому произвёл несколько сделок:

  1. по первой он купил контракт за 30 ден. ед., дающий ему право закупить муку на рынке по цене 7 завтра;
  2. второй контракт он продал за 50 ден. ед, позволив его держателю воспользоваться шансом купить его хлеб по цене 27 завтра.

а) Найдите прибыль фирмы в ситуации, если и владелец фирмы, и держатель второго контракта воспользуются ими.

Прогноз директора не сбылся, и цена хлеба на рынке завтра стала равна 24, а цена муки равна 6.
б) Найдите прибыль фирмы в реально сложившейся на рынке ситуации.

Решение

Прибыль фирмы: $\pi=p_{bread}\cdot q_{bread}-p_{flour}\cdot q_{flour}$
Текущая прибыль: $\pi=20\cdot10-2\cdot5\cdot10=100$
Владелец ожидает, что прибыль будет равна: $\pi=28\cdot10-2\cdot10\cdot10=80$
Поэтому он производит схему с контрактами. Если и владелец фирмы, и держатель второго контракта ими пользуются, то прибыль фирмы будет равна: $\pi=27\cdot10+50-2\cdot7\cdot10-30=150 \; \textbf{(6 баллов)}$

Однако реальная ситуация складывается таким образом, что держатель контракта на покупку хлеба им не пользуется, а закупает по цене 24. Так же случается и с мукой, он сам её закупает по рыночной цене. И тогда прибыль будет равна: $\pi=24\cdot10+50-2\cdot6\cdot10-30=140 \; \textbf{(5 баллов)}$

3. Две страны, один товар

В стране A на товар X предъявляют спрос две группы населения: функция спроса группы 1 имеет вид $Q_{D_1A}=100-2P$, функция спроса группы 2 имеет вид $Q_{D_2A}=50-3P$. Предложение товара X в стране A имеет вид $Q_{SA}=3P-10$. В стране B также производят товар X, спрос на него имеет вид $Q_{DB}=80-4P$, а предложение имеет вид $Q_{SB}=12P$.

а) Найдите равновесную цену и объёмы продаж в каждой из двух стран при отсутствии международной торговли.  
б) Предположим, что страны открыли торговые границы и начали импортировать и экспортировать товар X. Найдите новую равновесную цену при свободной торговле, а также объём экспорта и импорта для каждой страны.
в) Найдите изменение общественного благосостояния для страны A вследствие международной торговли. Кто выигрывает благодаря торговле – производители или потребители страны A?

Решение

В первую очередь необходимо рассчитать общую функцию спроса для страны A (1 балл):

$\begin{cases}Q_{DA}=150-5P, & P\leq\dfrac{50}{3} \\ Q_{DA}=100-2P, & \dfrac{50}{3}\leq P\leq50 \end{cases}$

Далее строятся графики спроса и предложения для обеих стран. Графически видно область равновесия для первой страны, поэтому приравнивая релевантную часть функции спроса к функции предложения, находим равновесие (2 балла).

Страна A будет импортировать, а страна B – экспортировать. Далее находим область цены, при которой будут равны объёмы экспорта и импорта. Эта область соответствует $Q_{DA}=150-5P$. Далее приравниваем совокупный спрос двух стран и совокупное предложение двух стран и получаем новое равновесие с $P_{FT}=10$, а также объёмом экспорта и импорта, равного 80 (4 балла).

Для того, чтобы найти изменение общественного благосостояния, нужно посчитать площадь фигуры, которая является суммой площади треугольника и трапеции (3 балла).

$\Delta TS=S_1+S_2=\dfrac{1}{2}\left(22-\dfrac{50}{3}\right)\left(\dfrac{200}{3}-40\right)+\dfrac{1}{2}\left(\dfrac{50}{3}-10\right)\left(\dfrac{200}{3}-40+100-20\right)=426\dfrac{2}{3}$

Благодаря торговле выигрывают потребители, так как их излишек растёт, а проигрывают производители, так как их излишек уменьшается (1 балл).
Графики для страны A и страны B, соответственно, выглядят следующим образом:

Изменение общественного благосостояния страны A:

4. Налоги монополиста

Спрос на продукцию фирмы-монополиста внутри страны задаётся функцией $Q_d=100-2P$, а её издержки $TC(q)=\dfrac{Q^2}{8}$. У монополиста также есть возможность реализовать продукцию на внешнем рынке по цене 25. Однако в силу квоты экспортируемое количество не может превышать 25. Жители внутри страны не имеют доступа к внешнему рынку.

а) Сколько единиц продукции будет реализовано на внутреннем рынке и по какой цене?
б) Государство вводит потоварный налог на монополиста (t единиц с каждой произведённой продукции). При какой ставке достигается максимум налоговых поступлений, чему он равен?

Решение


а). $\begin{cases} 50-q, & q\leq25 \\ 25, & 25\lt q\leq50 \\ 75-q, & 50\lt q\leq 75 \end{cases} \;\; \;\; \textbf{(1 балл)}$

$MC=0{,}25q$
Следовательно, пересечение с MR на участке $50\lt q\leq75$. MR не возрастает, MC строго возрастает и линейна. Следовательно, точка пересечения – точка максимума прибыли.

$\begin{array}{l}75-q=0, \; 25q \Rightarrow q^*=60 \textbf{ (1балл)} \\ q_{внешн}=25, \; q_{внутр}=35 \textbf{ (1балл)} \\ p_{внутр}=32{,}5 \textbf{ (1балл)} \end{array}$

Ответ может быть получен выписыванием функции прибыли и максимизации на участках. Штраф за отсутствие обоснования максимума – минус 1 балл.

б) Введение потоварного налога для монополиста эквивалентно изменению $MC:MC_1=0{,}25q+t$

Необходимо рассмотреть 3 случая. Во всех случаях MR не возрастает, MC строго возрастает и линейна. Следовательно, точка пересечения – точка максимума прибыли.

1 случай:
$\begin{equation} 50\leq q\leq75 \\ 75-q=0{,}25q+t \Rightarrow q=60-0{,}8t \Rightarrow t\leq12{,}5 \\ Tx(t)=60t-0{,}8t^2, \; t\leq12{,}5\end{equation}$

2 случай:
$\begin{equation} 25\leq q\leq50 \\ 0{,}25q+t=25 \Rightarrow q=100-4t \Rightarrow 12{,}5\leq t\leq\dfrac{75}{4} \\ Tx(t)=100t-4t^2, \; 12{,}5\leq t\leq\dfrac{75}{4}\end{equation}$

3 случай:
$\begin{equation}q\leq25 \\ 0{,}25q+t=50-q \Rightarrow q=40-0{,}8t \Rightarrow \dfrac{75}{4}\leq t\leq50 \\ Tx(t)=40t-0{,}8t^2, \; \dfrac{75}{4}\leq t\leq50 \\ Tx_{max}=Tx(t=12{,}5)=625\end{equation}$

Оценивание:
Вывод кривой Лаффера. По 1 баллу за каждый верный участок, всего 3 балла.
Максимум налоговых поступлений – 2 балла.
Оптимальная ставка потоварного налога – 2 балла.
Штраф за отсутствие обоснования максимума – минус 1 балл.
Максимум за задание – 11 баллов.

7-8 класс

1. Сбор ягод

Даша и Катя пошли в лес собирать ягоды. Даша за день может собрать 4 килограмма черники или 8 килограмм земляники, Катя же за день собирает 3 килограмма черники или 9 килограмм земляники. Девочки собирают ягоды с постоянной скоростью и могут собрать нецелое количество килограмм любого вида ягод. Какое максимальное количество земляники девочки вместе смогут принести домой, если бабушка попросила их собрать не меньше трёх килограммов черники для домашних заготовок варенья?
Решение

У Даши сравнительное преимущество в сборе черники, она и соберет все три килограмма черники (3 балла),и еще 2 килограмма земляники (3 балла). Катя собирает весь день землянику и приносит домой 9 килограмм ягод (4 балла). Итого, суммарно получается 11 кг земляники (1 балл).

2. Молодой инвестор

Молодой инвестор Уоррен хочет заработать свои первые деньги, вложив средства в банк. Всего у него есть 1000 долларов. У него есть три варианта сделать это:

  • Первый – открыть долларовый счёт со ставкой 5 % годовых.
  • Второй – открыть счёт в евро со ставкой 12 % годовых.
  • И третий – открыть счёт в рублях со ставкой 15 % годовых.

Обменные курсы доллара (кол-во долларов в 1 единице другой валюты) на текущий момент представлены в таблице (они останутся такими же и через год):

Купля
(Уоррен продаёт валюту)		 Продажа
(Уоррен покупает валюту)
Евро 1,9 2
Рубль 0,045 0,05

Уоррен выбирает альтернативу, которая принесёт ему наибольший доход через год, причём в итоге он хочет иметь на руках только доллары. Сколько долларов на руках будет у Уоррена через год?

Решение

Посчитаем прибыли от всех вариантов.
Первый вариант: Уоррен заработает 50 долларов = 0,05 × 1000 (3 балла).
Второй вариант: Уоррен заработает 64 доллара (переводим доллары в евро
по курсу продажи и потом обратно по курсу купли) $ \frac{1000}{2}\times1,12 \times1,9 = 1064$ (4 балла).
Третий вариант: Уоррен заработает 35 долларов $ \frac{1000}{0,05}\times 1,15 \times 0,045 = 1035 $
(3 балла).
Уоррен выберет второй вариант. У Уоррена на руках будет 1064 доллара
(1 балл).

3. Спортивные автомобили

Функция предложения фирмы-производителя спортивных автомобилей линейна. Известно, что повышение рыночной цены на спорткар с 200 до 260 тысяч евро увеличивает величину предложения с 5 единиц до 8 единиц. Определите величину излишка товаров, образующегося на рынке при цене 220 тысяч евро, если известно, что по такой цене потребители готовы купить 4 автомобиля?
Решение

Пусть функция предложения $Q_S = c + dP$.
Восстанавливаем функцию предложения по двум данным в условии точкам, имеем систему:
$\left\{ \begin{align}
8=c+260d\\
5=c+200d
\end{align} \right.$ (3 балла)

$P=100+20Q$ (3 балла)
При цене 220 величина предложения равна 6, а величина спроса равна 4 (по условию), следовательно, профицит равен двум автомобилям (5 баллов).

Обоснованно полученная верная функция предложения без составления системы оценивается в 6 баллов.

4. Аренда квартиры

Юрий Олегович собирается сдавать квартиру. Он может сдавать её посуточно или на длительный срок. В первом случае Юрий Олегович вынужден раз в 3 дня уходить с работы на 2 часа раньше, чтобы встретить новых жильцов. Помимо этого, раз в 3 дня нужно проводить уборку: хозяин квартиры может делать это сам, затрачивая 3 часа рабочего времени, или нанять себе помощницу бабу Маню, вместе с которой они управятся за 2 часа его рабочего времени. За одну уборку баба Маня берёт 300 рублей. Если же Юрий Олегович решит сдавать квартиру на длительный срок, отвлекаться от работы на встречу жильцов и уборку не придётся. При этом стоимость аренды составит 25 тысяч в месяц. Определите, при какой стоимости аренды за сутки Юрию Олеговичу безразлично, по какой схеме сдавать квартиру, если его рабочий день составляет 8 часов, а зарплата – 500 рублей в час. Считайте, что в любом месяце 30 рабочих дней.

Решение

Потери от уборки самостоятельно составляют 500 × 3 = 1500, от уборки с бабой Маней = 2 × 500 + 300 = 1300 < 1500. Значит, убираться они будут вдвоём (2 балла)
Сдавая квартиру посуточно и уходя с работы пораньше, владелец дополнительно теряет из своей зарплаты 2 × 500 = 1000 раз в три дня. Итого потери от сдачи квартиры посуточно составляют (1000 + 1300) × 10 = 23 000, где 10 – это количество раз в месяц, которое придется встречать жильцов и убираться (4 балла).
В альтернативном варианте, где квартира сдаётся на долгий срок, Юрий Олегович получает 25 000.
Обозначим за X стоимость посуточной аренды квартиры, тогда
(–23 000) + 30X = 25 000 → X = 1600 (5 баллов).

9 класс

1. Юный финансист

Юный финансист Фрэнк, думая о своем будущем, решает, как выгоднее всего сохранить до окончания школы накопленные к концу 9-го класса 100 ливро.
Его друг Элджернон предлагает сделку: сейчас Фрэнк даёт другу 100 ливро взаймы, а ровно через два года, к окончанию 11-го класса, получает от Элджернона 200 ливро.
Второй альтернативой является «Супервыгодный» двухлетний ливровый вклад в банке под 40% годовых (проценты начисляются каждый год на всю сумму, лежащую в банке).
Третий вариант самый изощрённый: Фрэнк может перевести ливро в иностранную валюту – тюбинги, – и открыть вклад «Забугор» так же на два года. Проценты по вкладу «Забугор» начисляются каждый год на всю сумму по ставке 20 % годовых. Сейчас один тюбинг можно купить за 20 ливро.
По прогнозам никогда не ошибающихся аналитиков, через два года (как раз тогда, когда истечёт срок вклада «Забугор») эта цена вырастет до 30 ливро за тюбинг. Сколько ливро на руках будет у Фрэнка через 2 года, если он максимизирует доход?
Решение

Сравним суммы, полученные через 2 года (к концу 11-го класса) в результате реализации каждой из альтернатив.
Если Фрэнк отдаст 100 ливро Элджернону, сумма будет равна 200 ливро.
Если Фрэнк откроет вклад «Супервыгодный», сумма будет равна $100\times (1,4)^2$ ливро (4 балла).
Открывая вклад «Забугор», Фрэнк положит на него 100 / 20 = 5 тюбингов (1 балл). Через 2 года на вкладе будет сумма $5\times(1,2)^2$ тюбинга. Итоговая сумма в ливро: $7,2\times30=216$ливро (5 баллов).
Значит, самой выгодной альтернативой будет открытие вклада «Забугор» (1 балл), и у Фрэнка будет 216 ливро на руках.

2. Страна Оз

Настоящий президент страны Оз считает, что открытость экономики – залог процветания государства. Поэтому страна ведёт свободную торговлю в единой валюте с соседом – королевством Роз. Единственным торгуемым товаром являются воздушные шары. Спрос жителей страны Оз, заядлых путешественников и авантюристов, на шары описывается функцией: $Q^O_d=2000-30P$, где $P$ — цена за один шар. Предложение внутренних производителей: $Q^O_s=100+4P$.
a) Известно, что в результате торговли установилась цена $P^*$ = 50 за воздушный шар. Будет ли страна Оз импортировать или экспортировать воздушные шары из королевства Роз? Определите объём импорта/экспорта.
б) В результате государственного переворота к власти в королевстве Роз пришёл король, являющийся давним неприятелем президента страны Оз, и издал указ запретить любого рода связи с соседним государством. Президент, озаботившийся благосостоянием граждан Оз, которые теперь будут вынуждены покупать любимые шары по другой цене, спросил совета у министра финансов. Министр сказал, что выходом из ситуации может быть введение субсидий для отечественных производителей. Помогите министру посчитать размер субсидии, которая приведёт к образованию на внутреннем рынке цены, равной прежней (50). Каковы при этом будут объёмы внутреннего производства и потребления воздушных шаров?
Решение

а) Внутренняя цена в стране Оз равна $\frac{950}{17} > 50$, следовательно, стране Оз выгодно импортировать шары по цене 50.
Тогда при цене 50 избыточный спрос страны Оз равен
(2000 – 30 × 50) – (100 + 4 × 50) = 500 – 300 = 200.
Это и есть объём импорта из королевства Роз (6 баллов).
б) Если цена на рынке должна остаться прежней, объём спроса не должен измениться, он равен 2000 - 30 × 50 = 500. Таким же должен быть и объём предложения. Обозначим размер субсидии за $s$. Нужно решить уравнение: 100 + 4(50 + s) = 500 (2 балла). Отсюда получаем, что необходимый размер субсидии равен 50 (2 балла). Объём предложения в этом случае равен спросу: 500 воздушных шаров (1 балл).

3. Авиакомпания "Т8"

Авиакомпания «T8» собирается первой выполнять рейсы между городами A и B. Сейчас в салоне самолёта установлено ровно 200 кресел эконом-класса и ни одного кресла бизнес-класса. Авиакомпания может без издержек заменить эконом-места бизнес-местами в пропорции 2:1, т.е. 2 кресла эконом-класса
на 1 место бизнес-класса. Спрос на билеты эконом- и бизнес-класса описывается функциями $Q^e=360-2P^e$ и $Q^b=80-P^b$ соответственно. Авиакомпания устанавливает цены таким образом, чтобы все места были распроданы. Все издержки постоянны и равны $С$ за рейс в случае его выполнения и 0 иначе. При каком максимальном $С$ авиакомпания готова выполнять рейсы?
Решение

Найдем зависимость количества эконом- и бизнес-кресел математически:
$Q^b=\dfrac{200-Q^e}{2}=200-2Q^b$ (3 балла).
Выручка компании:
$TR=(180-0,5Q^e)Q^e+(80-Q^b)Q^b=$
$=(180-0,5(200-2Q^b))(200-2Q^b)+(80-Q^b)Q^b=$
$=2(80+Q^b)(100-Q^b)+(80-Q^b)Q^b= $
$=2(8000-80Q^b+100Q^b-(Q^b)^2)+80Q^b-(Q^b)^2=$
$=(16000+40Q^b-2(Q^b)^2)+80Q^b-(Q^b)^2= $
$=-3(Q^b)^2+120Q^b+16000$ (4 балла), откуда максимум $(Q^b)^*=20 \to (Q^e)^*=200-2*20=160$, (1 балл).
$Pr^*=-3*400+120*20+16000-C=17200-C \to C_{max}=17200$ (3 балла).

4. Ставка налога и количество фирм

Спрос на некотором рынке задаётся функцией: $Q_d(p)=50,6-p$. Предложение каждой фирмы: $Q_s(p)=\max\{p-5;0\}$, фирм на рынке $n$. Государство вводит потоварный налог на потребителей, максимизируя налоговые сборы. Как и на сколько процентов изменится оптимальная налоговая ставка, если количество фирм увеличится вдвое?

Решение

Находим равновесие с учётом потоварного налога на потребителей:
$Q_d^1=50,6-p-t=Q_s=n(p-5)$

$p^*=\dfrac{50,6-t+5n}{n+1}$

$Q^*=n\left(\dfrac{50,6-t+5n}{n+1}\right)$ (5 баллов).

Суммарные налоговые сборы: $T=t\times Q=\dfrac{n}{n+1}(45,6t-t^2)$ (5 баллов).

Максимизирующее налоговые сборы значение $t^*$ не зависит от $n$ (1 балл).