1. Задача 2 ОЧ-2015 (10 класс)

Рассмотрим классическую дилемму современного человека: с одной стороны – поддержание физической формы на определенном уровне, а с другой – удовольствие от потребления торта. Пусть уровень физической формы Антона зависит положительно от количества часов, проведенных в спортзале (переменная x), и отрицательно – от единиц съеденного тортика (переменная y): $F(x,y)=x^{2}-xy-y^{2}+73$. Антон точно уверен, что он не проведёт в спортзале больше $3$ часов. Однако Антон желает, чтобы при любом времени, проведенном в спортзале и удовлетворяющем вышеописанным условиям, уровень его физической формы не падал ниже $9$ условных единиц. Определите максимально возможное при этом количество единиц потребленных тортиков.

В задании не предполагается целочисленность переменных.

Решение

Переформулируем задачу в виде математической модели. От нас требуется найти максимальное значение y, при котором $F(x,y)$ будет $\ge 9$ при любом $x\le 3$.

Сразу заметим, что наши переменные принимают только неотрицательные значения.

Рассмотрим функцию $f(x)=x^{2}−xy−y^{2}+73−9=x^{2}−xy−y^{2}+64$. Найдем y, при которых эта функция будет $\ge 0$ при любом $x\le 3$. Для этого нужно рассмотреть 3 случая.

Во-первых, решить систему (это случай, когда x не меньше 3):

\begin{cases}
f(3)\ge 0\\
x_{вершины} \ge 3 \\
\end{cases}

Решение системы : $\left[6;\dfrac{\sqrt{301}-3}{2}\right]$

Во-вторых, рассматриваемая $f(x)$ будет неотрицательной при условии $D \le 0:$

$$D=y^{2}−4(64−y^{2})=5y^{2}−256\le 0$$
$$y \in \left[−\dfrac{16}{\sqrt{5}};\dfrac{16}{\sqrt{5}}\right]$$

В-третьих, нерассмотренным остается случай, когда x меньше 3: единственное подходящее в этом случае значение – 0. Тогда $y \in [−8;8]$

Объединяя три наших случая и учитывая неотрицательность, получаем $y\in [0;8]$.

Тогда наибольшее количество единиц тортика, которое может потребить Антон при заданных условиях, равно 8.

2. Задача 1 ОЧ-2015 (10 класс)

Фирма «Три Угла», расположенная в стране N, занимается выращиванием волшебных цветов. Волшебные цветы растут сами, так что все издержки фирмы связаны только со строительством забора вокруг поля, на котором она растит свои цветы. Стоимость установки одного метра забора равна $\sqrt[4]{3}$ денежных единиц. Фирма может огородить забором поле любой площади, однако по законам страны N это поле обязательно должно быть треугольным (зато треугольник может быть любым: прямоугольным, тупоугольным, остроугольным). На поле площадью один квадратный метр вырастают 10 волшебных цветов.

1. Единственным покупателем волшебных цветов является король страны N. Король хотел бы приобрести 1000 волшебных цветов. Укажите минимальную цену одного цветка (в денежных единицах), при которой фирма «Три Угла» не понесет убытков, выполняя заказ короля.

2. Предположим, что заказы от короля больше не поступают, однако есть рынок, на который фирма «Три Угла», являющаяся монополистом, может поставлять свои цветы. Рыночный спрос описывается функцией: $P=4\sqrt{27}(300−\dfrac{4\sqrt{27}Q}{100})$. Существенно изменились теперь и издержки фирмы. Строительство забора теперь оплачивается по следующей схеме. Каждый метр нового забора обходится фирме в 500∗l денежных единиц, где l – длина забора, построенного фирмой (т.е. если фирма построила всего 10 метров забора, то за каждый построенный метр она должна заплатить 5000 денежных единиц). Закон о треугольной форме полей никто не отменял. Сколько метров забора необходимо построить фирме, чтобы получить максимальную прибыль? Целочисленность выращиваемых цветков можно игнорировать.

Подсказка. Подумайте, у каких треугольников площадь будет максимальна (строгое доказательство не требуется).

Решение

Пункт 1.
Этап 1. При заданном периметре площадь треугольника поля максимальна, когда он является равносторонним (можно использовать данное утверждение как факт, без доказательства). В этом случае площадь поля следующим образом соотносится с его периметром:$S=\dfrac{1}{4*\sqrt{27}}*p^{2}$.

Этап 2. Чтобы выполнить заказ, требуется поле площадью 100 квадратных метров, следовательно, его периметр можно найти из соотношения:

$$100=\dfrac{1}{4*\sqrt{27}}*p^{2}$$
$$p=20*\sqrt[4]{27}$$
Стоимость возведения забора такой длины составит $\sqrt[4]{3}∗20∗\sqrt[4]{27}=60$ денежных единиц.

Прибыль фирмы: $PR=1000*price-60\ge 0; min P =\dfrac{60}{1000}=0,06$.

Ответ: $0.06$ д.е.

Пункт 2.

Количество цветов связано с периметром следующим образом: $S=\dfrac{Q}{10}=\dfrac{1}{4*\sqrt{27}*p^{2}}.$

Тогда $Q=\dfrac{10}{4*\sqrt{27}p^{2}}$.

Прибыль фирмы:

$$PR=PQ-TC=4\sqrt{27}\left(300−\dfrac{4\sqrt{27}}{100}Q\right)Q−500p*p$$
$$PR=4\sqrt{27}\left(300−\dfrac{4\sqrt{27}}{100}*\dfrac{10}{4\sqrt{27}}p^{2}\right)\dfrac{10}{4\sqrt{27}}p^{2}-500p^{2}=\left(300−\dfrac{1}{10}p^{2}\right)10p^{2}-500p^{2}$$
$$PR=2500p^{2}−p^{$}=p^{2}(2500−p^{2})$$

Максимум прибыли достигается при периметре, равном $p=25\sqrt{2}$ метрам.

3. Задача 3 ОЧ-2015 (10 класс)

На одном из островов Большого моря располагаются две страны: Гамма и Дельта. Для удобства жителей и облегчения торговли страны используют единую валюту. В каждой стране производится и продаётся товар Б. В каждой стране на рынке присутствует большое число фирм. Параметры рынка представлены в таблице:

	Страна Гамма	Страна Дельта
Спрос	$Q^{d}=12-2p$	$Q^{d}=18-2p$
Предложение	$Q^{s}=2p-4$	$Q^{s}=2p-6$

1. Пусть страны имеют возможность для осуществления свободной торговли. Будут ли страны торговать между собой? Какая страна будет экспортёром, а какая – импортёром? Определите параметры равновесия (цену, величины экспорта и импорта, объёмы производств).

2. С целью поддержки национальных производителей страна Дельта ввела налог в размере 2,5 д.е. за ввоз каждой единицы товара Б. Определите новые параметры равновесия (цену, величины экспорта и импорта, объёмы производств, сумма налоговых сборов). Как изменилась совокупная выручка производителей товара Б страны Гамма по сравнению с пунктом 1?

3. Между странами существовала договорённость о беспошлинной торговле. Страна Дельта нарушила договор и ввела налог на ввоз товара Б. Чтобы не было вооружённого конфликта, этот налог на ввоз необходимо отменить. Однако тогда произойдёт спад производства товара Б в стране Дельта. Правительство страны Дельта решает ввести потоварную субсидию для национальных производителей. Какова должна быть величина субсидии, чтобы выручка национальных производителей была такой же, как и в пункте 2? Каковы будут бюджетные расходы на эту программу поддержки?

Как называется экономическая политика государства, описанная в пунктах 2 и 3?

Решение

Пункт 1.
$$\begin{array}{c}P_{Гамма}=4 \\ P_{Дельта}=6\end{array}$$
Цены на товары различаются, поэтому при отсутствии барьеров будет осуществляться международная торговля.

Суммируем предложение в двух странах и спрос в каждой из двух стран. (Аналогично можно находить функции экспорта и импорта)
$$\begin{array}{c}Q^{s}=Q^{d} \\
(2P−4)+(2P−6)=(12−2P)+(18−2P) \\
4P−10=30−4P \\
P=5\end{array}$$

Величины экспорта/импорта, объём производства Дельта и объём производства Гамма:
$$Exp = Imp = Q_{s}(5)−Q_{d}(5)=6−2=4$$
Производство: $Q^{s}(5)_{Гамма}=6 ;Q^{s}(5)_{Дельта}=4$

Страна	Гамма	Дельта
Роль	Экспортер	Импортер
Цена	5	5
Объем производства	6	4
Чистый экспорт	4	-4

Пункт 2.

Международная торговля осуществляться не будет, т.к. величина налога превышает разницу между ценами товаров в этих странах.
$$\begin{array}{c}Exp=Imp=0 \\
P_{Гамма}=4;Q_{Гамма}^{s}=4 \\
P_{Дельта}=6;Q_{Дельта}^{s}=6\end{array}$$

Сумма налоговых сборов: $0\cdot2,5=0$

Изменение выручки производителей страны Гамма $ = 6\cdot5−4\cdot4=30−16=14$

Пункт 3.

Прибыль национальных фирм является функцией от цены. Т.е. в зависимости от цены они продают то или иное количество продукции, т.к. рынок совершенно конкурентный.

Значит, им нужно установить такую субсидию, чтобы фактически цена для них равнялась 6 (цена при отсутствии международной торговли). Величина предложения совершенно конкурентной фирмы отвечает условию максимизации прибыли. Поэтому чтобы продавать 6 единиц, они должны получать 6 за каждую единицу продукции.

Тогда при наличии свободной торговли мы можем записать равенство спроса и предложения на международном рынке:

$$\begin{array}{c}Q_{s}=Q_{d} \\
6+(2P−4)=(12−2P)+(18−2P) \\
2+2P=30−4P \\
6P=28 \\
P=\dfrac{28}{6}=\dfrac{14}{3}\end{array}$$

Тогда необходимо дать потоварную субсидию в размере $6−\dfrac{14}{3}=\dfrac{4}{3}$

Расходы бюджета составят $6\cdot\dfrac{4}{3}=8$.

Пункт 4.
Протекционизм.

4. Задача 4 ОЧ-2015 (10 класс)

Г-н Комиссаренко решил преумножить свое богатство, положив 2 миллиона рублей в банк. Он выбирает между банками «Анжела» и «Виктория», годовые ставки по депозитам в которых составляют 5% и 20% соответственно. Однако с точки зрения рейтинговых агентств эти банки имеют разные категории надежности – А и B. Банк «Анжела» имеет категорию А, банк «Виктория» – категорию В. Банки категории А никогда не нарушают свои обязательства перед вкладчиками. Для банков категории B статистика хуже: в среднем ежегодно 10 из 100 таких банков прекращают платежи. Считайте, что неплатежеспособность банка может выявиться только по итогам первого квартала года, и к этому моменту вкладчик еще не получит никаких процентов, которые ему причитаются, так что в этом случае от его вклада не останется вообще ничего.

1. Рассчитайте ожидаемую сумму$^{*}$, которую г-н Комиссаренко будет иметь через год:

a. Вложив деньги в банк «Анжела»;

b. Вложив деньги в банк «Виктория»;

c. Поровну разделив деньги между банками.

2. На рынке появился третий банк «Светлана», его ставка по вкладу – 10%, а категория надежности – С, означающая, что банк окажется неплатежеспособным с вероятностью 5%.

Как появление нового банка повлияет на решение г-на Комиссаренко о выборе банка, при условии, что он должен положить деньги в один банк?

3. Государство ввело гарантию по банковским вкладам на сумму до 1,4 млн. рублей. Теперь в случае неплатежеспособности банка вкладчик получает сумму вклада в пределах 1,4 миллиона рублей и никаких процентов. А сумма вклада свыше 1,4 млн. рублей теряется, как и раньше. Вкладчик может иметь сколько угодно вкладов в разных банках, и гарантирован будет каждый вклад (главное, чтобы ни в одном банке не было больше 1,4 млн. руб.).

a. Куда при этих новых обстоятельствах, при прочих равных условиях, г-н Комиссаренко будет вкладывать свои 2 миллиона рублей?

b. Привело ли введение государственной гарантии по банковским вкладам к перетоку вкладов из менее надежных, с точки зрения рейтинговых агентств, банков в более надежные?

$^{*}$Под ожидаемой суммой следует понимать математическое ожидание.

Справка

Пусть распределение вероятностей случайной величины Х представлено в таблице:

Значения, которые принимает X	$X_{1}$	$X_{2}$	...	$X_{n}$
Вероятность	$p_{1}$	$p_{2}$	...	$p_{n}$

Математическим ожиданием $(E(X))$ случайной величины X называют число: $E(X)=p_{1}X_{1}+p_{2}X_{2}+...+p_{n}X_{n}.$

Пример. Предположим, вам предлагают сыграть в лотерею, где с вероятностью 110 вы выиграете 100 рублей, с вероятностью 12 вы выиграете 200 рублей, и с вероятностью 25 выиграете 500 рублей. Тогда математическое ожидание денежного выигрыша в этой лотерее равно: $E(X)=110∗100+12∗200+25∗500=10+100+200=310$ рублей.

Решение

Пункт 1.

Рассчитайте ожидаемую сумму, которую г-н Комиссаренко будет иметь через год:

Вложив деньги в банк «Анжела»; $E(A)=1,05∗Х$,где X−сумма вклада

При $Х=2$ млн. получаем: $2∗(1+0,05)=2,1$

Вложив деньги в банк «Виктория»; $E(В)=0,9∗1,2∗X=1,08X$

При $Х=2$ млн. получаем: $2∗(1+0,2)∗0,9=2,16$

$0,1$ – вероятность дефолта

$0,9$ – не дефолт

Поровну разделив деньги между банками.

Самый простой способ расчета состоит в получении среднего арифметического от ожидаемой суммы в двух банках:

$(2,1+2,16)/2 = 2,13.$

Таким образом, наиболее выгодно для вкладчика положить все деньги в банк В.

Пункт 2.

На рынке появился третий банк «Светлана», его ставка по вкладу – 10%, а категория надежности – С, означающая, что банк окажется неплатежеспособным с вероятностью 5% и средства вкладчика в течение года не будут ему возвращены. Как появление нового банка повлияет на решение г-на Комиссаренко о выборе банка, при прочих равных условиях?

$Е(С)=(0,95∗1,1)∗Х=1,045Х$

При $Х=2$ млн. получаем: $2∗(1+0,1)∗0,95=2,09$

Положив деньги в банк С, г-н Комиссаренко с вероятностью 95% получит 2,2 млн. руб., и с вероятностью 5% – 0 руб, ожидаемая сумма составит 2,09 млн. руб. Так как ожидаемая сумма и в банке А, и в банке В выше, чем в банке С, то появление банка С не повлияет на выбор вкладчика.

Пункт 3.

Государство ввело гарантию по банковским вкладам на сумму до 1,4 млн. рублей. Теперь в случае неплатежеспособности банка вкладчик получает только сумму вклада в пределах 1,4 миллиона рублей. А сумма вклада свыше 1,4 млн. рублей теряется, как и раньше. Вкладчик может иметь сколько угодно вкладов в разных банках, и гарантирован будет каждый вклад (главное, чтобы ни в одном банке не было больше 1,4 млн. руб.).

Как эти новые обстоятельства могут повлиять, при прочих равных условиях, на решение г-на Комиссаренко?
$$E(C)=
\begin{cases}
X+0.95*X*0,1=1,095X, & X\le 1.4\\
0.95*X*1.1+0.05*1.4=1.045X+0.07, & X \gt 1.4 \\
\end{cases}
$$
$$E(B)=
\begin{cases}
X+0.9*X*0,2=1,18X, & X\le 1.4\\
0.9*X*1.2+0.1*1.4=1.08X+0.14, & X \gt 1.4 \\
\end{cases}
$$
$$E(A)=1.05X$$

Ожидаемые суммы в банках В и С при введении государственной гарантии по вкладам увеличились, а в банке А – нет. Следовательно, привлекательность банков В и С в глазах г-на Комиссаренко по сравнению с банком А повысилась. Это может побудить г-на Комиссаренко к переводу денег из банка А в банки В и С.

Таким образом введение государственного страхования вкладов привело к тому, что депозиты стали перетекать в более рискованные банки. Следовательно, государственная гарантия по банковским вкладам поощряет переток депозитов в более рискованные банки.

2 млн. в А: 1,05*2=2,1

1,4 в А и 0,6 в В: 1,05*1,4+1,18*0,6=2,178

1,4 в А и 0,6 в С: 1,05*1,4+1,095*0,6=2,127

2 млн. в В: 1,08*2+0,14=2,3

1,4 в В и 0,6 в А: 1,18*1,4+0,6*1,05=2,282

1,4 в В и 0,6 в С: 1,18*1,4+1,095*0,6=2,309

2 млн. в С: 1,045*2+0,07=2,16

1,4 в С и 0,6 в А: 1,095*1,4+0,6*1,05=2,163

1,4 в С и 0,6 в В: 1,095*1,4+1,18*0,6=2,241

Таким образом, г-ну Комиссаренко выгоднее положить 1,4 млн. рублей в банк «Виктория» и 0,6 млн. руб. в банк «Светлана». Если необходимо разместить вклад целиком в одном банке, то предпочтение отдается банку «Виктория».

11 класс

1. Задача 1 ОЧ-2015 (11 класс)

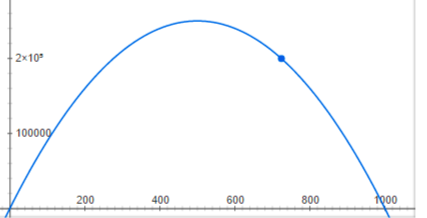
Население некоторого острова составляет ровно n человек. Самый бедный получает 0,01% всего дохода страны. Доход следующего жителя выше дохода предыдущего ровно на 0,02 процентных пункта. Найдите коэффициент Джини в данной стране.

Правитель данного острова, который, безусловно, является самым богатым жителем, убежден, что высокое неравенство вредит экономике острова в долгосрочном периоде. Однако в текущий момент времени, как вы уже, наверное, посчитали, ему принадлежит лишь малая часть доходов.

Правитель раздумывает законным способом отнять часть доходов у своего населения. Если это произойдет, и правитель попытается нарушить сложившееся распределение доходов, возмущенное несправедливостью население немедленно объединится в одну партию. После присвоения правителем части доходов населения объединенная партия разделит оставшиеся доходы поровну между n−1 членом партии.
Функцию полезности правителя можно охарактеризовать следующим уравнением:
$$U(G;a)=10(a+1)-1000G^{2},$$
где G - коэффициент Джини на острове, выраженный в долях; a – доля доходов правителя в общем доходе острова, выраженная в процентах (5%, а не 0.05, например).
Определите долю доходов правителя, которая максимизирует его уровень полезности. Захочет ли правитель ограбить население и присвоить часть его дохода? Если да, то какую долю дохода он присвоит?

Примечание:
$$1^{2}+2^{2}+3^{2}+...+n^{2}=\dfrac{n(n+1)(2n+1)}{6}$$

Решение

1. Определим, сколько человек живет на острове.
Пусть $a_{i}$ – доля (в %) дохода i-ого островитянина в общей доле доходов острова.
Используя формулу n-ого члена арифметической прогрессии $(a_{n}=a_{1}+d(n-1))$, а также очевидный факт, что сумма всех долей жителей должна составлять 100% получаем систему уравнений:
\begin{cases}
a_{n}=0.01+0.02(n-1)\\
\dfrac{0.01+a_{n}}{2}n=100\\
\end{cases}
Решая, которую получаем, что $n=100, a_{100}=1,99%.$

2. Вычисление индекса Джини.
Каждый индивид образует группу, которая составляет 1% в общей численности населения.
Доли доходов индивидов соответственно равны : 0,01%; 0,03%; 0,05%…1,97%;1,99%.

Накопленные доли доходов тогда равны: 0,01%; 0,01%+0,03% ;0,01%+0,03%+ 0,05%; …;…1,97%+1,99%.

Вычислим площадь под кривой Лоренца (S), которая состоит из одного треугольника и 99 трапеций: $S=12\times[1\times0,01+1\times(0,01+(0,01+0,03))+1\times((0,01+0,03)+ (0,01+0,03+0,05))+⋯ ]$

Выражение в квадратных скобках можно преобразовать следующим образом: каждая из долей 0,01%; 0,03%; 0,05%…1,97%;1,99% входит в него 1 раз (когда появляется впервые) плюс число раз, равное удвоенному количеству скобок, в которые она входит после первого своего появления.

Поэтому:

$$[…]=0,01(1+2∗99)+0,03(1+2∗98)+0,05(1+2∗97)+⋯+1,97(1+2∗1)+1,99$$
$$0,01+0,03+⋯+1,99=100$$
$$2(0,01∗99+0,03∗98+⋯1,97∗1)=$$
$$=2(0,01∗99+(0,01+0,02)∗98+⋯(0,01+0,02∗98)∗1)$$
$$0,01∗(99+98+⋯+1)=1+992∗99∗0,01$$
$$0,02∗(98+97+⋯+1)=1+982∗98∗0,02$$
$$0,02∗(97+96+⋯+1)=1+972∗97∗0,02$$
$$...$$
$$[…]=2∗(−0,01∗1+992∗99+0,02∗12∗[(1+99)∗99+(1+98)∗98+⋯+(1+1)∗1])=$$
$$=2(−0,01∗1+992∗99+0,01(1+992∗99+(992+982+⋯+12))=$$
$$=2∗(992+982+⋯+12)=33∗199$$
Итак, $S=12∗(33∗199+100).$
Тогда коэффициент Джини равен $G=1-\dfrac{S}{0.5\times100\times100}=0.3333.$

3. Стоит ли правителю что-либо менять?
Напомним, что a – доля доходов правителя в общем доходе острова. После объединения $99$ человек в одну партию и равномерного распределения доходов между ее членами правитель останется наиболее богатым на острове. Поэтому индекс Джини теперь будет равен:
$S=12∗99∗(100−a)+12∗1∗(100−a+100)=5050−50a$ - сумма площади треугольника с катетами $99$ и $(100-a)$ и площади трапеции с основаниями $(100-a)$ и $100$.
$$
G=1-\dfrac{S}{0.5\times100\times100}=\dfrac{a-1}{100}
$$
Тогда функция полезности правителя будет равна:
$U=10(a+1)-1000\times\left(\dfrac{a-1}{100}\right)^{2}$

Максимум этой функции достигается при $a=51%$. И полезность будет равна $U=517,5$
Полезность до действий правителя была равна $U=−81,18889$.
Сравнивая полезности, получаем, что правителю выгодно нарушить существующее распределение доходов (точное значение функции полезности вычислять необязательно, можно просто сказать, что выражение $10∗(1,99+1)−1000∗0,33332<517,5$).

2. Задача 2 ОЧ-2015 (11 класс)

Иван Федоров – владелец книжного интернет-магазина в стране Читалия. Он давно думал о расширении ассортимента, и, узнав о том, что в 2015 году исполняется 120 лет со дня рождения Сергея Есенина, Иван решил начать продажу аудиокниг с произведениями этого поэта.

Иван выяснил, что аудиокниги с произведениями С. Есенина будут интересны двум группам потребителей со следующими функциями спроса: $q_{1}=50-p_{1}$ и $q_{2}=40-2p_{2}$.

Издержки на разработку нового раздела сайта и приобретение оригинала аудиозаписи составили 200 читаликов (читалики – денежные единицы Читалии). 2 читалика с каждой проданной аудиокниги Иван обязан перечислять автору оригинала аудиозаписей.

Продажа будет устроена таким образом, что покупатели смогут скачивать аудиокнигу прямо с сайта магазина. Для этого Ивану необходимо оплатить как минимум один сервер – $85$ читаликов. Максимальная пропускная способность одного такого сервера составляет $40$ скачиваний. Если спрос на аудиокниги неожиданно окажется высоким, Иван может оплатить дополнительные серверы, за каждый из которых также придется заплатить $85$ читаликов.

Естественно, количество продаваемых аудиокниг может быть только целым числом.

1) Допустим, что Иван решил продавать аудиокниги обеим группам по единой цене. Найдите количество продаваемых копий, их цену и прибыль Ивана.

2) Допустим, что есть возможность продавать аудиокниги разным сегментам по разным ценам. Какими будут объемы продаж, цены и прибыль в этом случае?

3) Изменится ли число продаваемых аудиокниг в ситуациях 1) и 2), если теперь Иван сможет оплачивать каждый сервер всего лишь за 1 читалик. Если да, то как? Если нет, то почему?

Решение

Функция рыночного спроса:
$$q_{рын}=
\begin{cases}
90-3p&, p<20\\
50-p&, 20\le p<50 \\
\end{cases}
$$
Издержки, которые несет Иван:
$FC=200+85∗n$, $n$ - количество используемых серверов
$$VC=2Q$$
Ситуация 1. Единая цена для двух групп
Прибыль фирмы:
$$Pr=(30-13Q)\times Q-2Q-200-85n \to max$$
$$(30−23Q)-2=0$$
Количество, максимизирующее прибыль фирмы: $Q^{*}=42$. Тогда цена, которую Иван должен назначить, составляет $p^{*}=30-\dfrac{1}{3}∗42=16$. Заметим, что полученная цена удовлетворяет первому участку функции рыночного предложения.
Также полезно заметить, что мы нашли именно максимум прибыли, потому что функция прибыли - парабола, ветвями вниз.
Однако с одним сервером Иван не сможет продавать весь этот выпуск. Таким образом, перед ним встает вопрос: продавать только $40$ аудиокниг, оплачивая только $1$ сервер, или дополнительно приобрести еще один сервер и продавать оптимальное количество.
Сравним прибыли Ивана в этих двух случаях.
Если используется $1$ сервер:
$Pr=(30-\dfrac{1}{3}∗40)∗40-2∗40-200-85∗1=\dfrac{905}{3}=301\dfrac{2}{3}$
Если используются 2 сервера:
$Pr=(30-\dfrac{1}{3}∗42)∗42-2∗42-200-85∗2=218$
Поэтому Ивану выгоднее использовать только $1$ сервер. Его прибыль при этом составит $Pr=301\dfrac{2}{3}$.
Проверим второй участок предложения:
$$Pr=(50-Q)*Q-2Q-200-85n\to max$$
$$(50-2Q)-2=0$$
Количество, максимизирующее прибыль фирмы: $Q^{*}=24$. Тогда цена, которую Иван должен назначить, составляет $p^{*}=50−24=26$. Заметим, что полученная цена удовлетворяет второму участку функции рыночного предложения.
При $Q^{*}=24$ Ивану потребуется всего $1$ сервер. Его прибыль составит:
$Pr=24∗26-2∗24-200-85∗1=291$. Это меньше, чем максимальная прибыль в предыдущем пункте.
Ситуация 2. Разные цены для двух групп.
$$Pr=(50-q_{1})∗q_{1}+(20-\dfrac{1}{2}q_{2})∗q_{2}-2(q_{1}+q_{2})-200-85n\to max⁡(q_{1},q_{2})$$
Функция прибыли - сумма двух парабол ветвями вниз. Максимум прибыли достигается, если каждая из парабол достигает максимума. Это происходит при условиях:
$$(50-2q_{1})-2=0$$
$$(20-q_{2})-2=0$$
Т.е. при $q_{1}=24$ и $q_{2}=18$. Суммарное продаваемое количество $Q=24+18=42$, что требует использования двух серверов. Тогда прибыль фирмы составит:
$$Pr=(50-24)∗24+(20-12∗18)∗18-2(24+18)-200-85∗2=368$$
Как и в первом случае, необходимо сравнить полученную прибыль с прибылью, которую можно получить, используя только один сервер. Тогда необходимо решить следующую задачу:
$$Pr=(50-q_{1})∗q_{1}+(20-\dfrac{1}{2}q_{2})∗q_{2}-2(q_{1}+q_{2})-200-85n\to max(q_{1},q_{2})$$
$$\text{при условии } q_{1}+q_{2}=40$$
Выражая одно количество через другое и подставляя в функцию прибыли, получаем:
$$Pr=(50-(40-q_{2}))∗(40-q_{2})+(20-\dfrac{1}{2}q_{2})∗q_{2}-2∗40-200-85n\to max⁡(q_{2})$$
$$Pr=(10+q_{2})(40-q_{2})+20q_{2}-\dfrac{1}{2}q_{2}^{2}−280−85=50q_{2}−\dfrac{3}{2}q_{2}^{2}+35$$
$$50−3q_{2}=0$$

Оптимальное количество в этом случае: $q_{2}=\dfrac{50}{3}=16\dfrac{2}{3}$. Однако количество продаваемых аудиокниг, естественно, может быть только целым числом. Поэтому необходимо сравнить два ближайших целых значения:
1) $q_{2}=16$

Тогда $q_{1}=40-16=24. p_{1}=50-24=26;p_{2}=20−12∗16=12.$

Прибыль фирмы составит: $Pr=50∗16-\dfrac{3}{2}∗16^{2}+35=451$

2)$q_{2}=17$

Тогда $q_{1}=40−17=23. p_{1}=50-23=27;p_{2}=20−\dfrac{1}{2}∗17=11\dfrac{1}{2}.$

Прибыль фирмы составит: $Pr=50∗17−\dfrac{3}{2}∗17^{2}+35=451\dfrac{1}{2}.$

Таким образом, прибыль с использованием одного сервера превосходит прибыль при использовании двух серверов. Поэтому прибыль Ивана составит $451\dfrac{1}{2}$. Будет продано $q_{2}=17$ по цене $p_{2}=11\dfrac{1}{2}$ и $q_{1}=23$ по цене $p_{1}=27$.

3) Если аренда сервера теперь составляет $1$ читалик.

Ситуация 1: $PR_{1 сервер}=301\dfrac{2}{3}+85−1=385\dfrac{2}{3}; PR_{2 сервера}=218+85∗2−2=386.$

Теперь выгоднее продавать $42$ аудиокниги, используя $2$ сервера.

Ситуация 2: $PR_{1 сервер}=451\dfrac{1}{2}+85−1=535\dfrac{1}{2}; PR_{2 сервера}=368+85∗2−2=536.$

Теперь выгоднее использовать два сервера. Продавать $q_{1}=24$ и $q_{2}=18.$

3. Задача 4 ОЧ-2015 (11 класс)

В 1950-е годы экономисты обнаружили положительную взаимосвязь между уровнем инфляции и отклонением фактического совокупного выпуска от потенциального. Эту зависимость стали впоследствии называть кривой Филлипса$^{1}$:

$$
\pi-\pi^{e}=b*(Y-Y^{*})
$$

где $\pi$ – фактический уровень инфляции; $\pi^{e}$ – ожидаемый уровень инфляции; Y –фактический совокупный выпуск; $Y^{*}$ – потенциальный совокупный выпуск; b – положительный параметр.

В экономике некоторой страны $\Phi$ есть Центральный Банк. Часто для описания предпочтений Центрального Банка вводят функцию потерь L, которую Центральный Банк минимизирует. Глава ЦБ не любит инфляцию, но любит, когда в стране экономический подъем (фактический ВВП превышает потенциальный):
$$
L=\alpha(\pi-\pi^{*})^{2}-(Y-Y^{*})
$$
где $\pi^{*}$ – целевой уровень инфляции, который Центральный Банк считает наиболее благоприятным для экономики (постоянный параметр в рамках этой задачи); $\alpha$ – положительный параметр.

Будем предполагать, что гипотеза рациональных ожиданий верна, т.е. в равновесии ожидаемая инфляция равна фактической.

Взаимодействие между экономическими агентами и Центральным Банком происходит следующим образом:

1) Сначала экономические агенты формируют свои ожидания $(\pi^{e})$, минимизируя следующую функцию потерь: $(\pi-\pi^{e})^{2}$.

2) После этого Центральный Банк узнает выбранный уровень ожиданий и выбирает уровень инфляции $\pi$.

Предполагается, что Центральный Банк может непосредственно выбирать уровень инфляции и совокупного выпуска, которые ему необходимы. Также предполагается, что единственное ограничение, при котором Центральный Банк минимизирует свою функцию потерь, − это кривая Филлипса.

Вопросы:

1. Изобразите кривую Филлипса в координатах $(Y;\pi)$, предполагая, что $\pi^{e}=\pi^{*}$. Отметьте точку $(Y^{*};\pi^{*})$. Нарисуйте кривую безразличия Центрального Банка, (т.е. все комбинации $(Y;\pi)$, при которых L принимает фиксированное значение), проходящую через точку $(Y^{*};\pi^{*}))$. Чему равно значение функции потерь ($L^{*}$) в этом случае?

2. Предполагая, что ожидания не меняются $(\pi^{e}=\pi^{*})$, определите, выгодно ли будет Центральному Банку такое состояние экономики, в котором значения совокупного выпуска и инфляции составят $(Y^{*};\pi^{*}))$? Может ли он уменьшить свои потери при таких ожиданиях? Рассчитайте уровень инфляции и выпуска, которые выберет Центральный Банк. (Подсказка: посмотрите на график, который вы построили в предыдущем пункте. Подумайте, в каком направлении уменьшается значение функции потерь, попробуйте построить различные кривые безразличия).

3. Теперь вспомните, что по условию задачи экономические агенты формируют рациональные ожидания, т.е. в равновесии фактический уровень инфляции должен быть равен ожидаемому. Изобразите кривую Филлипса, для которой это условие выполнено. Какое равновесие установится в экономике? Возможна ли ситуация, в которой Центральному Банку лучше, а остальным экономическим агентам не хуже?

Рассмотренный в этой задаче cюжет в экономической литературе получил название проблемы временной несогласованности монетарной политики.

$^{1}$ Вероятно, если вы ранее сталкивались с кривой Филлипса, то вы рассматривали отрицательную взаимосвязь инфляции и безработицы. Однако несложно понять, например, в силу закона Оукэна, что это эквивалентно положительной взаимосвязи инфляции и отклонения выпуска от потенциального.

Решение

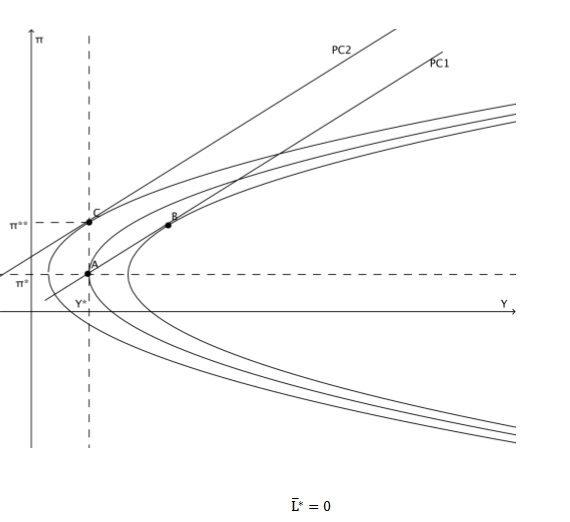
2. Если $\pi^{e}=\pi^{*}$, то ограничение для Центрального Банка – кривая Филлипса PC1. Т.к. $L=\alpha(\pi−\pi^{*})2−(Y−Y^{*})$, то при росте Y, значение функции потерь ЦБ снижается, поэтому чем правее расположена кривая безраличия, тем лучше для ЦБ. Поэтому при ограничении PC1 равновесие установится в точке B.

3. Равновесие должно установится в точке С: выпуск находится на уровне потенциального, а кривая Филлипса и кривая безразличия ЦБ касаются в этой точке.

В равновесии выпуск находится на уровне потенциального: это следует из кривой Филлипса $\pi=\pi^{e}$, поэтому $Y=Y^{*}$.

Кривая Филлипса и кривая безраличия ЦБ касаются, поэтому ЦБ невыгодно отклонятся и это равновесие.

Теперь найдем точки B и C:

Точка B:
$$
L=\alpha(\pi-\pi^{*})^{2}-(Y-Y^{*})\to min
$$
при $\pi−\pi^{*}=b\times (Y−Y^{*})$ (мы воспользовались тем, что $\pi^{e}=\pi^{*}$).

Решая эту задачу (можно просто подставить ограничение в целевую функцию), получаем, что $Y_{B}=Y^{*}+\dfrac{1}{2\alpha b^{2}}; \pi_{B}=\pi^{*}+\dfrac{1}{2\alpha b}$. Значение функции потерь составит: $L_{B}=-\dfrac{1}{4\alpha b^{2}}$. Поэтому Центральный Банк улучшил свое положение, уменьшив функцию потерь.

Точка С:

Как мы показали выше, кривая безразличия и кривая Филлипса должны касаться в этой точке, а $Y=Y^{*}$.

Наклон кривой Филлипса: $Y'_{\pi}=\dfrac{1}{b}$; Наклон кривой безразличия: $Y'_{\pi}=2\alpha(\pi-\pi^{*})$.

Приравнивая наклоны, получаем условие для точки C: $\pi_{C}=\pi^{*}+\dfrac{1}{2\alpha b}.Y_{C}=Y^{*}. L_{C}=\dfrac{1}{4\alpha b^{2}}.$

8 класс

1. Задача 1 ОЧ-2015 (8 класс)

Владелец автосалона «Эх, прокачу!» предложил каждому из своих менеджеров по продажам выбрать для себя на предстоящий год один из трех вариантов системы оплаты труда:

Вариант 1. Вознаграждение менеджера составляет $6 000 в год независимо от количества проданных им автомобилей.

Вариант 2. Вознаграждение менеджера составляет $4 000 в год плюс $250 за каждый проданный в течение года автомобиль.

Вариант 3. Вознаграждение менеджера составляет $500 за каждый проданный автомобиль.

Каждый из менеджеров хорошо представляет, сколько автомобилей он способен продать за год, и стремится максимизировать свой доход. Известно, что из 8 менеджеров автосалона половина выбрала первый вариант, а половина — второй. Третий вариант не выбрал никто.

(а) Оцените, какой объем продаж (в автомобилях) следует ожидать владельцу автосалона в предстоящем году (укажите верхнюю и нижнюю границы ожидаемого объема).

(б) Владелец автосалона планирует в рамках сокращения кадров уволить двух менеджеров. Каких менеджеров ему следует увольнять: тех, кто выбрал первый вариант, или тех, кто выбрал второй?

Решение

(а) Решим неравенства и посмотрим, при каком количестве проданных автомобилей какой вариант обеспечивает наибольшую прибыль. Можно заметить, что 1 вариант предпочтительнее, если выбравший его менеджер продает наименьшее число автомобилей, а 3 – если наибольшее. Пусть X – кол-во проданных автомобилей. Тогда
$$6000≥4000+250X$$
$$X\le 8$$

Т.е. если менеджер продает меньше 8 автомобилей, то он предпочитает 1 вариант.

Далее посмотрим, когда он предпочитает 3 вариант второму.
$$500X \ge 4000+250X$$
$$X\ge 16$$

Таким образом,

· Первый вариант обеспечивает менеджеру максимальный доход, если он планирует продать от 0 до 8 автомобилей.

· Второй вариант обеспечивает менеджеру максимальный доход, если он планирует продать от 8 до 16 автомобилей.

· Третий вариант обеспечивает менеджеру максимальный доход, если он планирует продать 16 автомобилей или более.

Можно сделать вывод, что 4 менеджера планируют продать от 0 до 8 машин, а еще 4 менеджера — от 8 до 16. Таким образом, планируемый объем продаж автосалона составляет от 32 до 96 автомобилей.

(б) Первый вариант выбирают наименее производительные менеджеры. При прочих равных увольнять нужно их.

2. Задача 2 ОЧ-2015 (8 класс)

В фирме работают 100 человек. Эти 100 человек могут быть разбиты на две категории: опытные работники и новички. Кроме того, как среди опытных работников, так и среди новичков, есть и мужчины, и женщины. О них известна следующая информация:

	Вся фирма	Мужчины	Новички
Число людей	100	60	40
Средняя зарплата	870	950	625

1. Определите среднюю зарплату опытных работников женского пола, если известно, что мужчины-новички имеют среднюю зарплату в размере 700, а всего мужчин-новичков 10 человек.

2. Можно ли утверждать, что женщины получают несправедливо более низкую зарплату по сравнению с мужчинами?

Решение

1. Составим на основе известных данных вспомогательную таблицу:

	Вся фирма	Мужчины	Новички	Женщины	Опытные
Число людей	100	60	40	40=100-60	60=100-40
Средняя зарплата	870	950	625	750=30000/40	3100/3=62000/60
Сумма зарплаты по категории	87000	57000	25000	30000=87000-57000	62000=87000-25000

· Чтобы рассчитать среднюю зарплату опытных работников женского пола, нам потребуются их суммарная зарплата и их численность.

· При этом нам известна суммарная зарплата мужчин-новичков: 7000. Тогда суммарная зарплата женщин-новичков равна 25000-7000=18000, а суммарная зарплата опытных женщин равна 30000-18000=12000.

· Аналогично определяется и численность опытных женщин. Для начала находим, что женщин-новичков 40-10=30 человек, потом рассчитываем численность опытных женщин: 40-30=10 человек.

· Тогда средняя зарплата опытных женщин составит: 12000/10=1200.

2. С одной стороны, средняя зарплата мужчин выше, чем у женщин. Однако, у ситуации есть и другая сторона. Для наиболее правильного ответа на этот вопрос перегруппируем наши данные в следующую таблицу:

	Мужчины-новички	Опытные мужчины	Женщины-новички	Опытные женщины
Число людей	10	50	30	10
Средняя зарплата	700	1000	600	1200

Таким образом, ответ на данный вопрос далеко не однозначен. Женщины-новички действительно получают меньше мужчин-новичков, но среди опытных работников средняя зарплата женщин выше, чем у мужчин.

3. Задача 3 ОЧ-2015 (8 класс)

Спрос на продукцию фирмы «Гамма» имеет вид $Q=1000−P$, где $Q$ — количество товара (в штуках), $P$ — цена товара (в рублях за одну штуку). Фирма «Гамма» стремится получить максимальную выручку от продажи товара. Руководство фирмы столкнулось с неожиданной проблемой: чтобы начать продажу товара, нужно установить на витрине ценник с указанием цены этого товара. Ценник набирается на специальном табло из соответствующих пластиковых цифр (представим, что никаких других путей оформления ценника не существует, например, нельзя написать цифры от руки). Однако большая часть цифр, из которых может быть собран ценник, оказалась утерянной. В распоряжении фирмы остались только четыре цифры: «1», «2», «2» и «7». Фирма может установить только такую цену на свою продукцию, которую можно собрать из этих цифр. Это означает, например, что фирма может установить цену 12, 221 или 127 рублей, но не может установить цену 57 рублей (так как у нее нет цифры «5») или 177 рублей (так как в ее распоряжении имеется всего одна цифра «7»). Какую цену установит фирма и сколько продукции она продаст?

Решение

Выведем функцию выручки.
$$TR=PQ=P(1000−P)=1000P−P^{2}$$
Зависимость выручки от цены представляет собой параболу с ветвями, направленными вниз, максимум которой достигается при цене, равной 500 рублям (это вершина параболы).

Парабола – симметричная функция, поэтому для максимизации выручки нам нужно среди всех чисел, которые может «собрать» фирма на ценнике, выбрать то, которое на числовой оси расположено ближе всех к числу 500. Это число 712.

4. Задача 4 ОЧ-2015 (8 класс)

Вам необходимо разгадать кроссворд и угадать загаданное слово из 9 букв, обозначающее банковскую операцию, в которой клиент расходует деньги сверх той суммы, которая есть у него на счете.

Решение кроссворда поможет угадать загаданное слово, которое состоит из букв, выделенных цветом. В задании оценивается и правильно угаданное слово, и каждое правильное слово в кроссворде.

По горизонтали:

1. Одна из форм материальных выплат, выплачиваемая государством населению.

2. Допускаемая норма чего-либо в рамках договора.

3. Превышение доходов бюджета над его расходами.

4. Исчисляемый в денежном выражении износ какого-то оборудования в процессе его использования.

5. Форма экономических взаимоотношений, при которых происходит перемещение товара от одного владельца к другому.

6. Денежные средства или иное имущество, вкладываемые в объекты предпринимательской и/или иной деятельности с целью получения прибыли.

7. Часть доходов, которая не тратится на текущие нужды, а откладывается на будущее

8. Расчет за купленные товары или услуги.

9. Различают экстенсивный и интенсивный типы экономического ..… .

10. Прибыль плюс издержки.

По вертикали:

1. Банкротство.

2. Организация рационального процесса передвижения товаров от поставщиков к потребителю.

3. Один из видов договоров, при котором одно лицо получает от второго лица в собственность деньги или товары, обязуясь вернуть их через определенный срок.

4. Экономический ….. – это относительная величина, помогающая проследить динамику какого-либо показателя.

5. Обязательство погасить чей-то счет в случае, если должник не сделает этого сам.

6. Еще один фактор производства, помимо традиционных капитала и труда, выделяемый некоторыми учеными в современной экономической науке.

7. Цена денежной единицы одной страны, выраженная в денежных единицах другой страны

8. Реализация готовой продукции компании.

9. Экономический ….. – это колебания уровня деловой активности, характеризующиеся такими фазами, как подъем, пик, спад и дно.

10. Социально-экономическое явление, при котором часть экономически активного населения не имеет работы, но активно ее ищет.

Решение

Получили буквы: ЕАТРОФРВД

Из них составляем требуемое слово. ОВЕРДРАФТ

9 класс

1. Задача 2 ОЧ-2015 (9 класс)

Спрос на продукцию фирмы «Гамма» имеет вид $Q=90−P$, $Q$ — количество товара (в штуках), P — цена товара (в рублях за одну штуку). Издержки производства каждой единицы товара составляют 10 рублей. Фирма «Гамма» стремиться получить максимальную прибыль от продажи товара. Руководство фирмы столкнулось с неожиданной проблемой: чтобы начать продажу товара, нужно установить на витрине ценник с указанием цены этого товара. Ценник набирается на специальном табло из соответствующих пластиковых цифр (представим, что никаких других путей оформления ценника не существует, например, нельзя написать цену от руки). Однако большая часть цифр, из которых может быть собран ценник, оказалась утерянной. В распоряжении фирмы остались только три цифры: «1», «2» и «8». Фирма может установить только такую цену на свою продукцию, которую можно собрать из этих цифр. Это означает, например, что фирма может установить цену 1 рубль или 12 рублей, но не может установить цену 48 рублей (так как у нее нет цифры «4») или 22 рубля (так как в ее распоряжении имеется всего одна цифра «2»).

Производитель пластиковых цифр завод «Циферблат» готов продать фирме «Гамма» одну (и только одну) любую цифру на ее выбор. Назовите максимальную цену, по которой фирма «Гамма» согласится приобрести у «Циферблата» цифру. Какая это будет цифра?

Решение

Зависимость прибыли от цены представляет собой параболу с ветвями направленными вниз: $$PQ−10Q=P(90−P)−10(90−P)=100P−P^{2}−900,$$

максимум которой достигается при цене, равной 50 рублям.

Парабола – симметричная функция, поэтому для максимизации прибыли нам нужно среди всех чисел, которые может «собрать» фирма на ценнике, выбрать то, которое на числовой оси расположено ближе всех к числу 50. Если фирма «Гамма» не пользуется услугой «Циферблата», то это число 28. В этом случае прибыль составит 1116 рублей.

Если же фирма «Гамма» купит у «Циферблата» цифру «5», то она сможет установить цену на уровне 51 рубль. Это самая близкая к оптимуму из возможных цен, она обеспечивает самый большой прирост прибыли, поэтому за цифру «5» фирма «Гамма» согласится заплатить больше всего.

В этом случае прибыль без учета оплаты услуг «Циферблата» составит: 1599 рублей.

1599-1116=483

2. Задача 4 ОЧ-2015 (9 класс)

Издержки фирмы «Альфа» описываются следующей зависимостью:
$$
TC=
\begin{cases}
\dfrac{q^{2}}{2}, &0\le q\le 7\\
-27q+2q^{2}+115,5, & q \gt 7\\
\end{cases}
$$
Цена на продукцию фирмы не зависит от ее объема выпуска. Найдите функцию предложения фирмы «Альфа».

Решение

Цель фирмы – максимизация прибыли.

Поэтому она максимизирует функцию $PR=pq−TC$

Рассмотрим оптимальное поведение фирмы на каждом из участков функции

$$
\pi=
\begin{cases}
pq-\dfrac{q^{2}}{2}, &0\le q\le 7\\
pq-(-27q+2q^{2}+115,5), & q \gt 7\\
\end{cases}
$$

Найдем оптимальное количество в зависимости от цены на каждом из участков функции. (На каждом участке функция представляет собой параболу с ветвями вниз).

$$q^{*}=p, q\le 7$$
$$q^{*}=\dfrac{p+27}{4}, q>7$$

Осталось понять следующее. Функция предложения – зависимость $Q(P)$. То есть, чтобы задать функцию предложения, необходимо для каждого значения цены указать соответствующий ей оптимальный уровень выпуска. Рассмотрим, при каких ценах фирме «Альфа» выгодно производить до 7 единиц продукции, а когда более 7 единиц продукции.

Для этого подставим найденные функции $q(p)$ в функции прибыли. Решим неравенство.

$$pq− \dfrac{q^{2}}{2} \le pq-(-27q+2q^{2}+115,5)$$
$$p^{2}−\dfrac{p^{2}}{2} \le p\dfrac{p+27}{4}−(−27\dfrac{p+27}{4}+2\left(\dfrac{p+27}{4}\right)^{2}+115,5)$$
$$3p^{2}−54p+195\le 0$$
$$p^{2}−18p+65\le 0$$
$$p\in [5;13]$$

Таким образом, если цена меньше 5, то мы используем первый участок. Далее мы используем второй участок (т.е. производим $q^{*}=\dfrac{p+27}{4}$). Таким образом, получаем ответ.