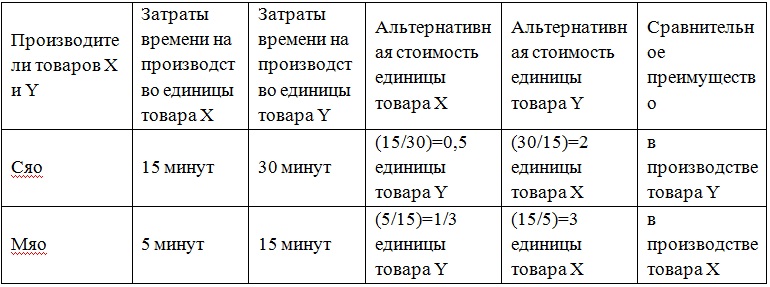
1. Бизнес на воде с сиропом
Определите размер партии воды, закупаемой Пончиком.
1) Если стоит цель максимизировать среднюю дневную прибыль, то задача решается так.
Предположим, что партия воды закупается на $t$ дней, тогда ее размер $100\cdot t$. Доход от продажи всей партии $TR =20\cdot 100\cdot t = 2000\cdot t$
Издержки состоят из расходов на закупку ($13\cdot 100\cdot t = 1300\cdot t$), расходов на транспортировку (300) и расходов на хранение.
Определим расходы на хранение.
Если Пончик закупает $100\cdot t$ бутылок воды, то в первый день расходы на хранение составят $2\cdot 100\cdot t$
К началу второго дня на складе будет $100(t – 1)$ бутылок воды. Следовательно, расходы на хранение во второй день равны $2\cdot100(t – 1)$. Рассуждая аналогично, расходы в третий и день $2\cdot100(t – 2)$, четвертый день $2\cdot100(t – 3)$ и т.д., расходы в t-й день составят $2\cdot100$. Последовательность расходов на хранение является арифметической прогрессией. Ее сумма:
$$S_t=\frac{(a_1+a_t)}{2t}=\frac{(2\cdot100\cdot t+2\cdot100)}{2t}=100(t+1)\cdot t$$ (1)
Запишем функцию средней дневной прибыли:
$$\pi=\frac{(2000t-1300t-300-100(t+1)t)}{t}=\frac{(600t-100t^2-300)}{t}=600-100t-\frac{300}{t} \to max$$ (2)
Равенство производной нулю достигается при $t=\sqrt3\approx1.73$. Вторая производная отрицательна, так что это – точка максимума.
Поскольку количество дней – целое число, то следует выбрать одно из двух значений $t=1$ или $t=2$ в зависимости от того, при каком из них прибыль больше.
$$\pi(1)=\frac{(20\cdot100-13\cdot100-300-2\cdot100)}{1}=200$$
$$\pi(2)=\frac{(20\cdot200-13\cdot200-300-100\cdot(2+1)\cdot2)}{2}=250$$
Очевидно, средняя дневная прибыль достигает максимума, если партия закупается на 2 дня. Значит, размер партии равен $100\cdot2 = 200$ бутылок.
Тот же результат может быть получен и методом перебора. Сразу заметим, что из формулы (2) следует, что более, чем 5-дневные партии рассматривать нет смысла, так как издержки хранения возрастают так сильно, что прибыль начиная с 6-дневной партии становится отрицательной.

*Рассчитывается по формуле (1)
Ответ: 200 бутылок.
2) Если стоит цель максимизировать прибыль в течение какого-то более длительного срока работы предприятия, чем один день ($Т$ дней, где $Т$ – целое число), то оптимальный размер партии определяется длинной периода $Т$.
Рассмотрим прибыль, которую получит Пончик за один закупочный период. Из таблицы (столбец 7) следует, что трехдневные парии можно не закупать, а заменить одну трехдневную партию тремя однодневными. Прибыль при этом будет одна и та же. Четырехдневную партию выгоднее заменить двумя двухдневными, тогда прибыль будет больше (500+500=1000 при двух двухдневных закупках против 500 при одной четырехдневной). Из тех же соображений пятидневную партию лучше заменить пятью однодневными. Таким образом, Пончику выгодно закупать либо однодневными, либо двухдневными партиями в зависимости от длины периода, в котором максимизируется прибыль.
Если период содержит четное число дней, то очевидно, максимальная прибыль будет обеспечена двухдневными партиями, так как среднедневная прибыль при этом достигает максимума.
Поскольку максимальная дневная прибыль достигается при двухдневных закупках, встает вопрос о целесообразности рассмотрения периодов, содержащих нечетное число дней. Если окажется, что в периоды с четным числом дней $T=2N$,$N=1,2,3$… прибыль всегда выше, чем в периоды с нечетным числом дней $T=2N+1$, Пончику будет выгодно заменить период с нечетным числом дней на период на один день более короткий, содержащий четное число дней.
Прибыль, полученная за период, содержащий четное число дней определяется следующим образом:
$$\pi_{t=2}(T)=250\cdot T, T=2N, N=1,2,3…$$
так как в этом случае закупки осуществляются двухдневными париями (200 бутылок), Пончик закупает воду каждые два дня и всю ее продает. Каждые два дня он получает прибыль 500 рублей, или в среднем в день 250 руб.
Прибыль, полученная за период, содержащий нечетное число дней, зависит от того, какими партиями производятся закупки воды.
Если закупки совершаются двухдневными партиями (200 бутылок), то для обеспечения продаж в течение $Т$ дней ($T=2N-1, N=1,2,3$…) придется закупать воду на $Т+1$ дней. В этом случае половина бутылок последней парии (100 бутылок) не будет продана, то есть прибыль за весь период будет меньше, чем при четном числе дней ($Т+1$) на величину выручки одного дня ($20\cdot100=2000$ руб.). Однако эти 100 бутылок и хранить нет смысла (лучше сразу от них избавиться так или иначе), чтобы не нести лишних расходов. А это уже увеличивает прибыль за период на величину затрат на хранение 100 бутылок в течение последнего закупочного периода, то есть на $2\cdot2\cdot100=400$ руб. :
$$\pi_{t=2}(T)=250\cdot(T+1)-2000+400=250\cdotT-1350, T=2N-1, N=1,2,3…$$
Однако, если сократить период на 1 день, то прибыль будет
$$\pi_{t=2}(T-1)=250\cdot(T-1)=250T-250,T=2N-1, N=1,2,3…$$
что выше, чем прибыль, полученная в периоде с нечетным числом дней.
Следовательно, если период содержит четное число дней, то закупки следует производить двухдневными партиями (200 бутылок), а периоды с нечетным числом дней выгодно заменять более короткими (на один день) периодами с четным числом дней, что позволит увеличить прибыль.
Если закупки производятся однодневными партиями (100 бутылок), то прибыль равна
$$\pi_{t=1}(T)=200\cdot T, T=2N-1,N=1,2,3…$$
Если заменить период на более короткий (Т-1), содержащий четное число дней, прибыль будет равна
$$\pi_{t=2}(T-1)=250\cdot(T-1)=250T-250,T=2N-1, N=1,2,3…$$
Такая замена периода на более короткий имеет смысл, если она не приводит к уменьшению прибыли, то есть:
$$\pi_{t=2}(T-1)=250\cdot(T-1)=250T-250\ge200\cdot T=\pi_{t=1}(T), T=2N-1, N=1,2,3… \Rightarrow T\ge5$$
Следовательно, при длительности периода, в котором максимизируется прибыль, превышающем 5 дней, максимум прибыли будет получен, если закупки производить двухдневными партиями (200 бутылок), а период с нечетным числом дней заменять на период на один день более коротким.
Для длительности периода меньше 5 дней запишем прибыль, получаемую при закупках однодневными и двухдневными партиями:

Очевидно, что при $Т<5$ следует в период, содержащий нечетное число дней, закупать воду однодневными партиями, а в период, содержащий четное число дней – двухдневными. При $Т=5$ и закупках однодневными партиями прибыль будет такая же, как и при $Т=4$ и закупках двухдневными партиями. Так что в этом случае можно сократить период на один день без потери прибыли.
Ответ: размер партии зависит от длительности периода, в течение которого максимизируется прибыль. Если этот период не превышает 4 дней, то для получения максимальной прибыли размер партии должен быть равен 100 бутылок, если число дней в периоде нечетное, и 200 бутылок, если число дней четное. Если же длительность периода превышает 4 дня, то Пончику закупать нужно только партиями по 200 бутылок, при этом длительность периода, в котором максимизируется прибыль, должна быть равна четному числу дней, в противном случае прибыль не будет максимальной.
2. Дискриминация и неравенство
$\frac{F}{0,5}=2F$ – число мужчин
$\frac{F}{0.6}=\frac{5}{3}F$ – число женщин
$\frac{5}{3}F-F=\frac{2}{3}F$ – число незамужних женщин
Число домашних хозяйств:
$F$ – домохозяйства-семьи,
$F$ – домохозяйства, состоящие из неженатых мужчин
$\frac{2}{3}F$ – домохозяйства, состоящие из незамужних женщин
Домохозяйства-семьи и домохозяйства, состоящие из неженатых мужчин, имеют одинаковый доходи одинаковую численность, поэтому объединим их в одну группу. Ее численность 2F, а доля в общей численности
$$\frac{2F}{(2F+\frac{2}{3}F)}=\frac{3}{4}=0,75$$
Доля домохозяйств, состоящих из незамужних женщин равна 0,25.
Если доход мужчины $Z$, то доход общества
$$Z\cdot2F+\frac{1}{3}\cdot Z\cdot\frac{2}{3}\cdot F=\frac{20}{9}\cdot ZF$$
Тогда доля доходов домохозяйств-семей и домохозяйств-неженатых мужчин в общем доходе:
$$\frac{2ZF}{(\frac{20}{9}\cdot ZF)}=0.9$$
Кривая Лоренца:
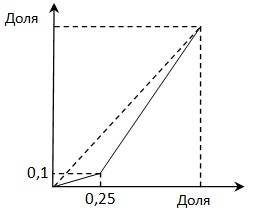
Коэффициент Джини $G=0.25-0.1=0.15$
3. Вкусняшки в лесном царстве
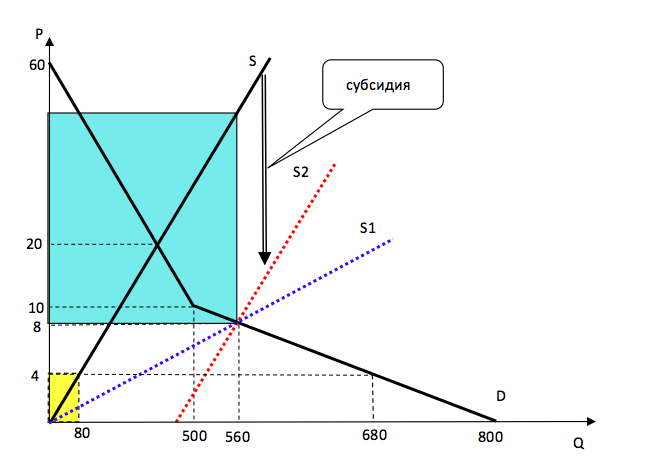
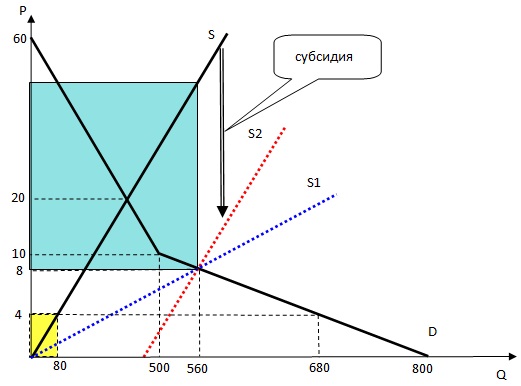
Большинство жителей лесного царства очень недовольны высокой рыночной ценой вкусняшек, и они делегировали Волка и Орла просить лесного царя Медведя посодействовать тому, чтобы сделать вкусняшки более доступными. Медведь не против и даже приказал выделить из царской казны $X$ тугриков для решения вопроса. Проблема только в том, как распорядиться этой суммой. Волк предлагает выплачивать производителям вкусняшек субсидию – $t$ тугриков за каждую проданную тонну. А Орел советует все выделенные деньги использовать на модернизацию производства, тогда по его оценкам непременно произойдет рост предложения вкусняшекаж на 250% при каждом уровне цен! Приглашенные эксперты – 33 попугая – провели исследование и вынесли вердикт - оба варианта, при прочих равных условиях, обеспечат одинаковое снижение рыночной цены вкусняшек. Однако они единогласно высказались в поддержку только одного варианта, исходя из предположения, что в будущем произойдет рост спроса на вкусняшки. В обоснование своей позиции они привели два весомых аргумента.
Определите:
а) какую сумму $X$ предполагается выделить из царской бюджета для поддержки производителей вкусняшек;
б) как и на сколько процентов изменится цена тонны вкусняшек, если из казны будет выделена оговоренная сумма;
в) за какой вариант расходования средств казны высказались 33 попугая, и каковы могли быть их аргументы.
Для этого сначала определим суммарную функцию спроса зверей и птиц на вкусняшки, преобразовав исходные функции спроса в функции вида $Q=f(P)$. Функция спроса зверей будет иметь вид $Q = 200 - 20P$, а функция спроса птиц $Q = 600 - 10P$.
Суммарный спрос будет описываться кусочно-линейной функцией:
\[\begin{cases}
600 - 10P, & \text{при }10\le P \le60; \\
800 - 30P, & \text{при }0 \le P \le10.\end{cases}\]
Определим исходную функцию предложения вкусняшек. Так как она линейная и имеет эластичность равную 1, то она выходит из начала координат. Если бы цена была зафиксирована на уровне 4 тугрика за тонну, то покупатели смогли бы купить (320/4=80) тонн вкусняшек (в соответствии с условиями задачи), но они готовы купить $800-30\cdot4=680$ тонн ( в соответствии с функцией спроса). При цене 4 тугрика на рынке был бы дефицит товара, а объем продаж определялся возможностями продавца предложить товар на продажу, т.е. функцией предложения. Отсюда следует, что график предложения проходит через точку с координатами (80; 4). Соответственно функция предложения имеет вид $Q = 20P$.
При цене 10 тугриков продавцы готовы продать 100 тонн вкусняшек, а покупатели готовы купить 500 тонн вкусняшек, на рынке возникнет дефицит товара, значит первоначальная равновесная цена должна быть больше 10 тугриков. Приравняв соответствующую функцию спроса и предложения, находим, что цена равна 20 тугриков.
2) Рассчитаем, какой станет новая цена вкусняшек.
Так как оба варианта реализации рекомендаций Волка и Орла приводят к одинаковому результату, то достаточно показать, как изменится функция предложение в результате реализации рекомендаций Орла – предложение должно вырасти в 3,5 раза при любых ценах. Получаем, что этот вариант изменения предложения даст новую функцию предложения $Q = 70P$. Чтобы получить новую равновесную цену мы снова должны приравнять функцию спроса и предложения, но теперь при цене 10 продавцы готовы продать 700 тонн вкусняшек, на рынке возникает излишек и равновесная цена будет меньше 10 тугриков. Приравняв соответствующую функцию спроса и предложения, находим, что цена будет равна 8 тугриков. Итак, цена снизится с 20 до 8 тугриков, т.е. снизится на 60%.
3) Определим ставку потоварной субсидии.
При цене 8 тугриков продавцы готовы продавать 560 тонн вкусняшек. Без субсидии и без модернизации производства данное количество товара они были готовы предложить по цене (560/20)=28 тугриков за тонну. 8 тугриков они получат от покупателей, а 20 тугриков им должна компенсировать царская казна. Таким образом, мы определили размер потоварной субсидии t=20 тугриков.
4) Оценим общую сумму субсидии.
Новому равновесию соответствует 560 тонн вкусняшек, за каждую проданную тонну из казны выделяют 20 тугриков, значит общая сумма субсидии $560\cdot20=11 200$ тугриков.
5) Возможные аргументы экспертов
• Субсидия только компенсирует издержки продавцов, ее придется выплачивать каждый год, в то время как модернизация производства непосредственно снижает издержки и поэтому достаточно разовой выплаты из царской казны.
• Если будет расти спрос, то вариант с субсидией в будущем приведет к большему росту цены, нежели вариант с модернизацией.
4. О целочисленности решения
Товар $X$ может выпускаться на станках двух типов. Один станок типа $A$ может произвести максимум 100 ед. товара в день, и его аренда стоит 100 денежных единиц в день. Один станок типа $B$ может произвести максимум 80 ед. в товара в день, и его аренда стоит 90 денежных единиц в день. Выпуск фирмы – не обязательно целое число.
а) Допустим, количество станков не обязательно целое. Сколько станков каждого типа следует арендовать фирме, чтобы произвести $Q$ ед. продукции в день и расходы на аренду были минимальны? Ответьте на вопрос для каждого $Q>0$.
б) Теперь допустим, что количество станков может быть только целым. Сколько станков каждого типа следует арендовать фирме, чтобы произвести $Q$ ед. продукции в день и расходы на аренду были минимальны при $Q=170$? $Q=240$?
в) Верно ли, что если в пункте а) оптимальным решением для фирмы является аренда a станков типа $A$, и a нецелое, то при учете целочисленности обоих типов станков оптимальным решением будет аренда $a^*$ станков типа $A$, где $a^*$ — одно из двух целых чисел, ближайших к $a$?
Таким образом, фирма минимизирует значение выражения $100a+90b$, выбирая любые неотрицательные $a$ и $b$, удовлетворяющие условию $100a+80b=Q$. Выражая $100a$ из условия и подставляя в формулу для издержек, получаем, что издержки равны $(Q-80b)+90b=Q+10b$. Эта функция возрастает по $b$, поэтому фирме следует выбрать минимально возможное значение $b$, то есть 0.
Следовательно, при любом $Q$ фирме оптимально арендовать 0 станков типа B и $Q/100$ станков типа А .
Можно было также заметить (второй способ решения), что при использовании станка типа А расходы на единицу продукции равны 1 ден. ед., а при использовании станка типа B — 9/8 ден. ед., и поэтому оптимальным является использование только станков типа А.
б) 170 единиц можно произвести тремя способами: (1) Арендовать 2 станка типа А; (2) арендовать 1 станок типа А и 1 станок типа B; (3) арендовать 3 станка типа B. Издержки для этих трех способов равны 200, 190, и 270 соответственно; следовательно, оптимальным является способ (2).
240 единиц можно произвести четырьмя способами: (1) Арендовать 3 станка типа А; (2) арендовать 2 станка типа А и 1 типа B; (3) арендовать 1 станок типа А и 2 типа Б; (4) арендовать 3 станка типа B. Издержки будут равны 300, 290, 280, и 270 единиц соответственно. Следовательно, оптимальным является способ (4).
в) Нет, неверно. Рассмотрим $Q=240$. В пункте (а) оптимальной является аренда 2,4 станков типа А и 0 станков типа B. C учетом же целочисленности в (б) мы получили, что оптимальной является аренда 0 станков типа А и 3 станков типа B, но 0 не является одним из двух целых чисел, ближайших к 2,4.
Примечание: для $Q=240$ ответ в условиях целочисленности не только не является одним из ближайших к ответу без ограничения на целочисленность, но и является диаметрально противоположным: если без ограничения на целочисленность нужно арендовать только станки типа А, то с ограниченим — только станки типа B. Данная задача (с ограничением на целочисленность) является частным случаем задачи о рюкзаке(См., например, https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B0_%D0%BE_%D1%80%D0%B0%D0%BD%D1%86%D...), с различными вариациями которой можно встретиться в самых разных областях экономики.
5. Одному хорошо, а в компании лучше?
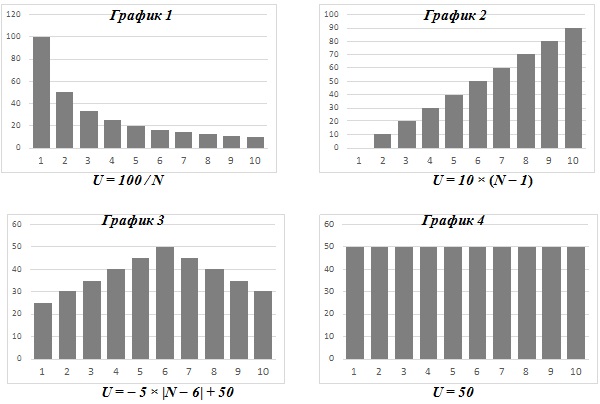
а) Приведите примеры благ, которые могли бы соответствовать графикам — по одному для каждого. Обоснуйте свой ответ.
б) Иногда при принятии решения о потреблении того или иного блага люди еще не знают точно, сколько других пользователей будут участвовать в потреблении. Например, отправляясь на горнолыжный курорт, человек может быть не в курсе, сколько других людей собираются туда в это же время, то есть насколько длинные будут очереди на подъемники.
Рассмотрим монополистов, предлагающих блага, соответствующие графикам 1—4. Каждый из монополистов предлагает свое благо, за использование или потребление которого он требует плату. У каждого блага есть по 10 потенциальных пользователей (потребителей). Каждый из них должен заплатить за участие в потреблении блага ту цену, которую назначит монополист. При этом любой пользователь принимает решение об оплате, когда он уже знает цену, назначенную монополистом, но не знает, сколько еще людей будут использовать это благо одновременно с ним.
Назовем излишком потребителя разницу между полезностью, которую он получает от блага, и уплаченной ценой. Человек, который не стал покупать благо, получает излишек 0. Назовем равновесием ситуацию, в которой каждый потенциальный потребитель повел себя так, чтобы его излишек был максимально возможным (с учетом выбора других участников). Если равновесий несколько, то будем считать, что реализуется то, в котором потребителей блага больше.
Найдите количество потребителей, которое будет у каждого блага в равновесии в зависимости от его цены (функцию спроса) Какая цена будет максимизировать выручку каждого монополиста?
- Ценность блага для потребителя обратно пропорциональна числу пользователей. Можно предположить, что речь идет о каком-то частном благе, которое делится поровну на всех его потребителей. Скажем, это может быть пицца, которая каждому потребителю приносит ценность 100, если съедена целиком, а отдельный кусок приносит полезность 100/N (если пицца разделена на N равных кусков).
Второй вариант интерпретации — демонстративное потребление (снобизм). Иногда потребители некоторых благ чувствуют себя хуже, если эти блага не эксклюзивны. Например, богатый человек, покупающий дорогую яхту, хотел бы быть единственным владельцем такой яхты в мире, и чем больше в мире еще таких яхт, тем менее его собственная яхта для него ценна.
- Если потребитель является единственным пользователем блага, то оно не приносит ему полезности. Далее, чем больше потребителей, тем больше полезность для каждого. Такие блага называются сетевыми: пользователи объединяются в сеть и общаются в ней друг с другом. Например, таким благом является телефон: он тем более ценен, чем большему количеству людей (обладателей такого же телефона) можно позвонить.
- При небольшом количестве пользователей это благо похоже на сетевое (ценность для каждого потребителя растет по мере увеличения их числа), а затем — на частное. Такие блага называются клубными: быть единственным пользователем неинтересно, но и слишком большому числу людей будет тесно. В качестве примера можно привести футбольную площадку, встречу любителей игры в карты и т. п.
- В этом случае представлен классический пример общественного блага, которое в полной мере обладает свойством неконкурентности: ценность для каждого потребителя не зависит от того, сколько других потребителей есть у данного блага. В качестве примера подойдет любое общественное благо: солнечный свет, национальная оборона, доска объявлений и т. п.
б) Пусть $P$ — цена блага, назначенная монополистом.
- Потребитель с номером N будет подключаться к потреблению блага, только если его излишек, равный $(100/N– P)$, не меньше 0 (если он равен 0, то потребитель подключится к потреблению из-за условия о реализации равновесия с максимальным числом участников). Значит, N потребителей подключатся, если цена не больше $100/N$, и тогда по определению обратная функция спроса имеет вид $P = 100/N$ (при целых N), а прямая:
\[N=\begin{cases}
0, & \text{если }P>100; \\
1, & \text{если }P\in(50;100]; \\
2, & \text{если }P\in(100/3;50]; \\
3, & \text{если }P\in(25;100/3]; \\
4, & \text{если }P\in(20;25]; \\
5, & \text{если }P\in(100/6;20]; \\
6, & \text{если }P\in(100/7;100/6]; \\
7, & \text{если }P\in(12,5;100/7]; \\
8, & \text{если }P\in(100/9;12,5]; \\
9, & \text{если }P\in(10;100/9]; \\
10, & \text{если }P\le10.\end{cases}\]
Выручка монополиста будет равна 100 при любой цене из множества (100; 50; 100/3; 25; 20; 100/6; 100/7; 12,5; 100/9; 10) — при таких ценах подключатся 1, 2, … 10 потребителей соответственно. При любой другой цене выручка будет меньше, так как подключившиеся потребители заплатят не максимальную цену. (Например, если цена 24, то подключатся 4 потребителя, как и при цене 25, но они заплатят меньше.)
Выручка монополиста будет равна 100 при любой цене из множества (100; 50; 100/3; 25; 20; 100/6; 100/7; 12,5; 100/9; 10) — при таких ценах подключатся 1, 2, … 10 потребителей соответственно. При любой другой цене выручка будет меньше, так как подключившиеся потребители заплатят не максимальную цену. (Например, если цена 24, то подключатся 4 потребителя, как и при цене 25, но они заплатят меньше.) - При цене $P$, не большей 90, всегда есть два равновесия: никто не пользуется и пользуются все. Действительно, если никто не подключился, то никто не сможет увеличить свой излишек, подключившись первым (у первого полезность равна 0). Если же хоть кто-то подключился, то выгодно подключиться всем (у остальных излишек будет еще больше, чем у первого). По условию, из двух равновесий будет реализовываться наилучшее для монополиста, так что выручка будет равна $10P$.Если цена больше 90, то не подключается (даже если подключатся все, они получат отрицательный излишек).
Получаем функцию спроса:
\[N=\begin{cases}
0, & \text{если }P>90; \\
10, & \text{если }P\le 90.\end{cases}\]
Значит, монополисту нужно установить максимально возможную цену (90). - Возможны 7 случаев, которые представлены в таблице.
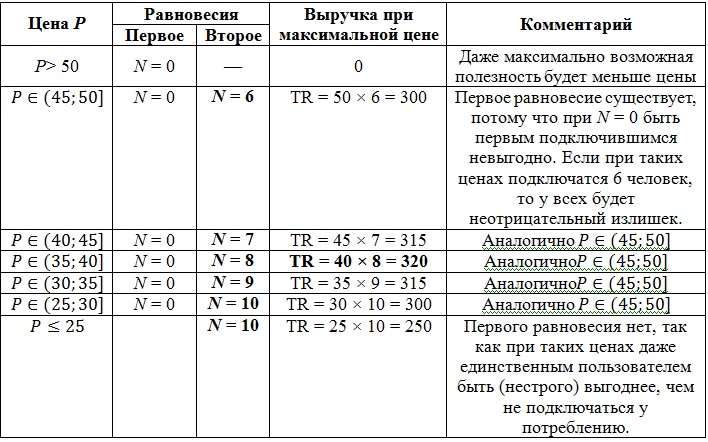
Получаем функцию спроса:
\[N=\begin{cases}
0, & \text{если }P>50; \\
6, & \text{если }P\in(45;50]; \\
7, & \text{если }P\in(40;45]; \\
8, & \text{если }P\in(35;40]; \\
9, & \text{если }P\in(30;35]; \\
10, & \text{если }P\le13.\end{cases}\]
Как видно из таблицы, максимальную выручку фирма получает, назначив цену 40. - Максимальная готовность платить каждого покупателя равна 50 независимо от их количества, следовательно, функция спроса имеет вид:
\[N=\begin{cases}
0, & \text{если }P>50; \\
10, & \text{если }P\le50.\end{cases}\]
Чтобы максимизировать выручку, фирме нужно назначить максимальную цену, при которой подключатся все 10 пользователей — цену 50.