1. Импортозамещение
| $\begin{array}{l} \; \: x_1 + y_1 = 190 \\ 2x_2+y_2 =80 \\ 3x_3+y_3 =90 \\ 4x_4+y_4 =140 \\ \end{array}$ |
Изначально страны свободно торгуют товарами. В равновесии производство товаров распределяется эффективно между странами, причем две страны производят только Икс, а две - только Игрек. Известно, что одна из четырех стран (назовем ее «страна $N$») экспортирует $100$ единиц Игрека.
- (12 баллов) Определите значение $K$. Какую страну мы обозначили буквой $N$?
- (6 баллов) В стране $N$ пришел к власти новый президент, основа программы которого - поддержка отечественного производителя и импортозамещение. Новый президент запретил импорт Икса, и страна перестала участвовать в мировой торговле. Определите, в какую сторону и на сколько единиц в результате этого изменилось потребление комплектов из $K$ единиц Икса и единицы Игрека в данной стране.
- (12 баллов) Определите, в какую сторону и на сколько единиц в результате событий пункта 2 изменилось суммарное потребление комплектов в остальных странах. (Считайте, что после исключения страны $N$ из торговли на мировом рынке установилось новое равновесие, и в нем производство товаров распределяется эффективно между торгующими странами.)
- Определить $K$ можно одним из двух способов.
Способ 1. При эффективном распределении производства товар производят те страны, в которых альтернативные издержки его производства минимальны.
В данном случае альтернативные издержки производства Икса равны 1, 2, 3 и 4 единицы Игрека в странах соответственно. Значит, товар Икс производят страны 1 и 2, а товар Игрек –– страны 3 и 4. Таким образом, общее производство Икса равно $190 + 80/2 = 230$, общее производства Игрека
равно $90 + 140 = 230$. Следовательно, товары потребляются
в пропорции $1 ∶ 1$, то есть $K = 1$.
Способ 2. Тот же результат можно было получить, построив суммарную КПВ (Рис. 1.2). Точка на КПВ, в которой две страны производят только Икс –– это вторая точка излома КПВ (если считать слева направо), ее координаты –– $(230; 230)$. Через нее и начало координат проходит прямая с наклоном $1$ (отсюда получается $K = 1$).
В странах 1 и 2 производится Икс, и поэтому они не экспортируют Игрек. Страна 3 производит $90$ единиц Игрека, и поэтому она не может экспортировать $100$ единиц. Значит, «страна $N$» –– это страна 4. - Поскольку страна 4 экспортирует $100$ единиц Игрека и производит $140$, для домашнего потребления остается $40$ единиц Игрека, а $40$ единиц Икса импортируется.
В отсутствие торговли (в условиях автаркии) страна 4 будет производить равное количество единиц Икса и Игрека (и потреблять столько же). Значит, $4x_4 + x_4 = 140$, откуда $x_4 =
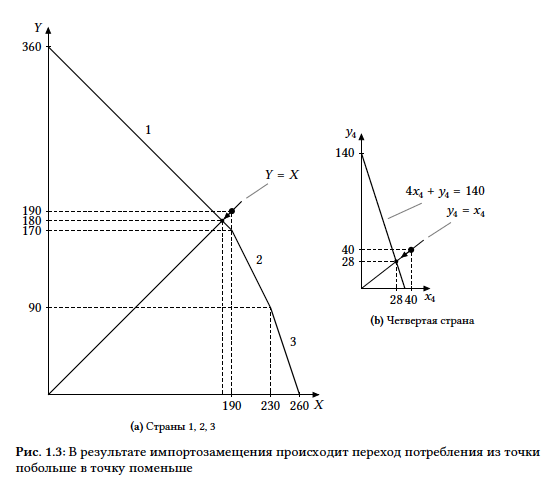
= y_4 = 28$. В условиях торговли страна потребляла по $40$ единиц Икса и Игрека. Значит, потребление комплектов из Икса и Игрека сократилось на $12$ единиц (Рис. 1.3b).
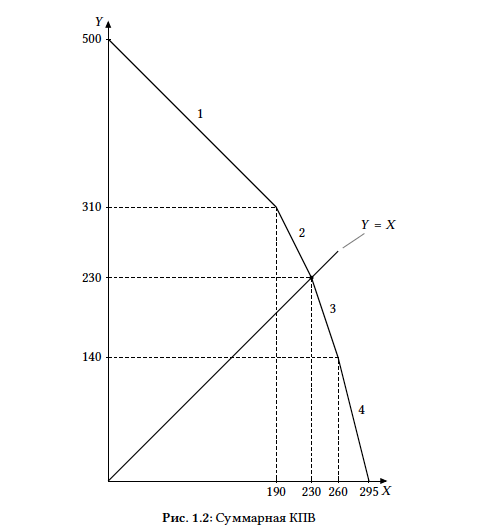
Этот результат не должен вызвать удивления: отказываясь от участия в торговле, страна лишает себя возможности покупать товар дешевле, чем ей обходится его производство. - В условиях торговли со страной 4 страны 1, 2 и 3 в сумме потребляли $230 − 40 = 190$ единиц Икса и Игрека. После исключения страны 4 из торговли объемы потребления будут определяться пересечением суммарной КПВ стран 1, 2 и 3 и прямой $Y = X$.
Суммарная КПВ стран 1, 2 и 3 является ломаной, соединяющей точки $(0; 360)$, $(190; 170)$, $(230; 90)$, $(260; 0)$, она представлена на Рис. 1.3a. Поскольку точка излома $(190; 170)$ лежит ниже прямой $Y = X$, пересечение будет достигаться на первом участке КПВ. Первый участок описывается уравнением $Y = 360 − X$, значит, точка пересечения удовлетворяет уравнению $360 − X = X$, откуда $X = 180$. Значит, суммарное потребление комплектов из Икса и Игрека в трех странах уменьшилось на $190 − 180 = 10$ единиц.
Этот результат не должен вызвать удивления: когда одна из стран отказалась от участия в торговле, остальные страны потеряли возможность покупать товар, в котором она имеет сравнительное преимущество.

Альтернативное решение
а) Поскольку страны свободно торгуют товарами, решить задачу можно, сделав предположения о возможных мировых о ценах этих товаров.
Если бы $p_Y>p_X$, то все страны, максимизируя свой доход, производили бы только товар Игрек (при этом каждая из стран), что не обеспечит требуемый баланс между объемами потребления товаров и не удовлетворит условию задачи о том, что только две страны производят этот товар.
Если бы $p_X>4p_Y$, то все страны, максимизируя свой доход, производили бы только товар Икс, что также не обеспечит требуемый баланс между объемами потребления и не удовлетворит условию задачи о том, что только две страны производят этот товар.
Если бы $p_Y\le p_X<2p_Y$, то вторая, третья и четвертая страны, максимизируя свой доход, производили бы только товар Игрек, что также не удовлетворяет условию задачи.
Если бы $3p_Y< p_X\le 4p_Y$, то первая, вторая и третья страны, , максимизируя свой доход, производили бы только товар Икс, что также не удовлетворяет условию задачи.
Единственной возможностью, при которой две страны будут производить товар Икс и две страны - товар Игрек, является ситуация, когда мировые цены соотносятся следующим образом: $2p_Y\le p_X\le 3p_Y$. Тогда товар Икс будут производить первая и вторая страны, а товар Игрек – третья и четвертая. Следовательно, будет произведено $190+40=230$ единиц товара Икс и $90+140=230$ единиц товара Игрек. Откуда сразу следует пропорция, в которой эти товары потребляются странами: на каждую единицу товара Икс должна приходиться одна единица товара Игрек.
Заметим, что соотношение между мировыми ценами в этом случае можно было бы найти, например, из торгового баланса 4-ой страны, которая продаст 100 единиц товара Игрек ради приобретения 40 единиц товара Икс (в этом случае 4-ая страна потребит 40 единиц каждого товара). Следовательно, $100p_Y=40p_X$, или $p_X-2.5p_Y$
в) Подход к решению аналогичен решению пункта а).
Если бы $p_Y>p_X$, то все страны, максимизируя свой доход, производили бы только товар Игрек, что не обеспечит требуемый баланс между объемами потребления товаров.
Если бы $p_X>3p_Y$, то все страны, максимизируя свой доход, производили бы только товар Икс, что также не обеспечит требуемый баланс между объемами потребления товаров.
Если бы $p_Y\le p_X\le 3p_Y$, то 1-ая страна производила бы только товар Икс в объеме 190 единиц и для удовлетворения требуемого соотношения потребовалось бы произвести 190 единиц товара Игрек, однако, даже если бы при сложившихся рыночных ценах обе страны производили бы только Игрек, то смогли бы произвести не более $90+80=170$ единиц. Что также не обеспечит требуемый баланс между объемами потребления.
Единственной возможностью, когда можно будет удовлетворить этот баланс, если 1-ая страна будет производить оба товара. Это возможно только при $p_Y= p_X$. Тогда 2-ая и 3-я страны произведут только товар Игрек в объеме 170 единиц. Учитывая соотношение в объемах потребления товаров, найдем, сколько Иксов и Игреков должна произвести 1-ая страна: $y=170+y_1=190-y_1$, откуда $y_1=10, x_1=180$. То есть, всего 180 комплектов, состоящих Икса и Игрека, произведет мировой рынок, состоящий из 1-ой, 2-ой и 3-ей стран.
2. Консультанты
Зарплата одного неопытного консультанта равна $100$ тыс. руб. в месяц, и предложение их услуг на рынке не ограничено (выпускников экономических и математических факультетов –– множество). Опытные же консультанты –– редкий вид, их приходится с трудом переманивать из конкурирующих компаний, и поэтому найм каждого следующего обходится дороже. Чтобы нанять $L$ опытных консультантов, фирме нужно затратить $L \cdot (240 + L)$ тыс. руб. в месяц. Всего в следующем месяце фирма собирается выполнить $Q$ проектов.
- (15 баллов) Допустим, $Q = 25$. Сколько опытных и неопытных консультантов ей
следует нанять, чтобы минимизировать издержки на выполнение проектов? - (15 баллов) При каких значениях $Q$ фирма не будет нанимать неопытных консультантов?
- Пусть $q_1$ - количество проектов, на которые фирма будет ставить неопытных консультантов вместе с опытными, а $q_2$ - количество проектов, на которые фирма будет ставит только двух опытных консультантов, $q_1 + q_2 = Q$. Обозначим за $l$ количество неопытных консультантов, за $L$ –– количество опытных. Тогда $l = 3q_1$, $L = q_1 + 2q_2$. Затраты компании на услуги труда консультантов равны
$$C = 100l + L \cdot (240 + L)$$
Нужно минимизировать эту функцию при ограничениях $l = 3q_1$, $L = q_1 + 2q_2$, $q_1 + q_2 = Q$. Эту задачу можно свести к задаче минимизации по одной переменной. Поскольку переменных у нас четыре ($q_1$, $q_2$, $l$ и $L$), это можно сделать четырьмя способами (на олимпиаде, конечно, достаточно представить один корректный способ решения).
Способ 1 (по $q_2$). Подставим выражения для $l$ и $L$ в целевую функцию:
$$C = 100l + L \cdot (240 + L) = 100 \cdot 3q_1 + 240(q_1 + 2q_2) + (q_1 + 2q_2)^2$$
Затем, подставляя $q_1 = Q − q_2$, получаем
$$C = 540(Q − q_2) + 480q_2 + (Q + q_2)^2 = q_2^2 − (60 − 2Q)q_2 + Q^2 + 540Q$$
Фирма минимизирует значение этого выражения по $q_2$ на отрезке $[0; Q]$. Относительно $q_2$ это парабола с ветвями вверх, и поэтому минимум издержек достигается в ее вершине $q^*_2 = 30 − Q$, если $q^*_2 ∈ [0; Q]$. Тот же ответ можно получить, взяв производную функции по $q_2$ $(C′ = 2q_2 − (60 − 2Q))$ и приравняв ее к $0$. В этом случае можно заметить, что производная в критической точке меняет знак с $−$ на $+$ (варианты: первая производная возрастает, вторая производная равна $2$, то есть положительна), так что это точка минимума.
При $Q = 25$ имеем $q^*_2 = 30 − 25 = 5 ∈ [0; 25]$.
Способ 2 (по $q_1$). Подставим выражения для $l$ и $L$ в целевую функцию:
$$C = 100l + L \cdot (240 + L) = 100 ⋅ 3q_1 + 240(q_1 + 2q_2) + (q_1 + 2q_2)^2$$
Затем, подставляя $q_2 = Q − q_1$, получаем
$$C = 540q_1 + 480(Q − q_1) + (2Q − q_1)^2 = q^2_1 + (60 − 4Q)q_1 + 4Q^2 + 480Q$$
Фирма минимизирует значение этого выражения по $q_1$ на отрезке $[0; Q]$. Относительно $q_1$ это парабола с ветвями вверх, и поэтому минимум издержек достигается в ее вершине $q_1^* = 2Q − 30$, если $q^*_1 ∈ [0; Q]$. Тот же ответ можно получить, взяв производную функции по $q_1$ $(C' = 2q_1 + (60 − 4Q))$ и приравняв ее к $0$. В этом случае можно заметить, что производная в критической точке меняет знак с $−$ на $+$ (варианты: первая производная возрастает, вторая производная равна $2$, то есть положительна), так что это точка минимума.
При $Q = 25$ имеем $q^*_1 = 50 − 30 = 20 ∈ [0; 25]$.
Окончание способов 1 и 2. Значит, на 5 проектов фирма отправит только опытных консультантов, а на 20 – группы из 1 опытного и 3 неопытных консультантов. Всего она наймет $l = 3q_1 = 60$ неопытных и $L = q_1 + 2q_2 = 30$ опытных консультантов.
Способ 3 (по $l$). Выразим $q_1$ и $q_2$ через $l$ и $L$. $q_1 = l/3$, и поэтому $L = q_1 + 2q_2 = l/3 + 2q_2$. Отсюда $q_2 = \frac{L − l/3}{2}$. Значит, ограничение $q_1 + q_2 = Q$ принимает вид $l/3 + \frac{L − l/3}{2} = Q$, то есть $l/6 + L/2 = Q$. Oтсюда $L = 2Q − l/3$. Подставляя это соотношение в целевую функцию, получаем
$$C = 100l + L \cdot (240 + L) = 100l + 480Q − 80l + (2Q−l/3)^2 = l^2/9 + (20 − 4Q/3)l + 480Q + 4Q^2$$
Фирма минимизирует значение этого выражения по $l$ на отрезке $[0; 6Q]$. Относительно $l$ это парабола с ветвями вверх, и поэтому минимум издержек достигается в ее вершине $l^* = 6Q − 90$, если $l^* ∈ [0; 6Q]$. Тот же ответ можно получить, взяв производную функции по $l$ $(C' = 2l/9 + (20 − 4Q/3))$ и приравняв ее к $0$. В этом случае можно заметить, что производная в критической точке меняет знак с $−$ на $+$ (варианты: первая производная возрастает, вторая производная равна $2$, то есть положительна), так что это точка минимума.
При $Q = 25$ имеем $l^* = 150 − 90 = 60 ∈ [0; 6 \cdot 25]$. Получаем тот же ответ, что выше: фирма наймет $60$ неопытных и $L^* = 2 \cdot 25 − l^*/3 = 30$ опытных консультантов.
Способ 4 (по $L$). Аналогично способу 3, получаем, что $l/6 + L/2 = Q$. Отcюда $l = 6Q − 3L$. Подставляя это соотношение в целевую функцию, получаем
$$C = 100l + L \cdot(240 + L) = L^2 + 240L + 100(6Q − 3L) = L^2 − 60L + 600Q$$
Фирма минимизирует значение этого выражения по $L$ на отрезке $[0; 2Q]$. Относительно $L$ это парабола с ветвями вверх, и поэтому минимум издержек достигается в ее вершине $L^* = 30$, если $L^* ∈ [0; 2Q]$. Тот же ответ можно получить, взяв производную функции по $L$ $(C' = 2L−60)$ и приравняв ее к $0$. В этом случае можно заметить, что производная в критической точке меняет знак с $−$ на $+$ (варианты: первая производная возрастает, вторая производная равна $2$, то есть положительна), так что это точка минимума.
При $Q = 25$ имеем $L^* = 30 ∈ [0; 2 \cdot 25]$. Получаем тот же ответ, что выше: фирма наймет $30$ опытных консультантов и $6 \cdot 25 − 3 \cdot 30 = 60$ неопытных консультантов. - Будем руководствоваться ответами, полученными в предыдущем пункте для произвольного $Q$.
Если фирма не нанимает неопытных консультантов, то $q_1 = 0$, $q_2 = Q$, $l = 0$, $L = 2Q$ то есть $q_1$ и $l$ должны лежать на левой границе допустимого интервала, а $q_2$ и $L$–– на правой.
Для этого вершина параболы, которую мы минимизировали в пункте 1, должна лежать или на соответствующей границе, или за ней (например, если получилось, что издержки минимизируются при $q_1 = 50$ и $q_2 = −10$, а при этом $Q = 40$, то нужно выбирать $q_1 = Q = 40$ и $q_2 = 0$).
В зависимости от способа решения пункта 1 (которое может быть в общем виде приведено в пункте 2, если пункт 1 решался для $Q = 25$) это будет или правая ($q_2 \ge Q$, $L \ge 2Q$), или левая ($q_1 \le 0$, $l \le 0$) граница найденного интервала.
Решая соответствующее неравенство ($q_1 = 2Q − 30 \le 0$ или $q_2 = 30 − Q \ge Q$ или $l = 6Q − 90 \le 0$ или $L = 30 \ge 2Q$), вo всех четырех случаях получаем $Q \le 15$.
Значит, фирма не будет нанимать неопытных работников, если общее количество проектов не больше $15$.
3. Неравенство олигархов
- (12 баллов) Назовем $10\%$ богатейших жителей страны олигархами. Выведите уравнение кривой Лоренца, отражающей распределение доходов среди олигархов. Иными словами, определите, какую долю $y$ суммарного дохода всех олигархов получает доля $x$ наиболее бедных олигархов. Что больше –– степень неравенства доходов среди олигархов или степень неравенства доходов во всей стране? (Степень неравенства будем измерять с помошью коэффициента Джини.)
Проверьте себя: полученная вами кривая Лоренца (как и всякая кривая Лоренца) должна проходить через точки $(0; 0)$ и $(1; 1)$. - (10 баллов) В стране $B$ кривая Лоренца описывается уравнением $Y = 1 − \sqrt{1 − X}$. Выведите уравнение кривой Лоренца, отражающей распределение доходов среди олигархов страны $B$ (олигархами здесь также называются $10\%$ богатейших жителей). Что больше –– степень неравенства доходов среди олигархов страны $B$ или степень неравенства доходов во всей стране?
- (8 баллов) Что больше – степень неравенства доходов среди $10 \%$ богатейших или среди $1 \%$ богатейших жителей страны $B$? Среди $1 \%$ богатейших или среди $0,1\%$ богатейших жителей страны $B$?
1) определить, какую часть составляет доход всех олигархов общем доходе страны;
2) определить, какую часть составляет доход доли $x$ наиболее бедных олигархов в общем доходе страны;
3) разделить второй показатель на первый.
- $90$% населения, не входящие в группу олигархов, получают долю $Y(0,9) = 0,81$ всего дохода, а олигархи, следовательно, получают $1 − Y(0,9) = 0,19$ всего дохода.
Доля $x$ наиболее бедных олигархов составляет долю $0,1x$ от всего населения страны. При этом вместе с $90$% неолигархов они составляют $0,9+0,1x$ населения и получают $Y(0,9+0,1x) = (0,9 + 0,1x)^2$ всего дохода; без учета неолигархов они получают $Y(0,9 + 0,1x) − Y(0,9) = (0,9 + 0,1x)^2 − 0,9^2 = 0,18x + 0,01x^2$ всего дохода.
Значит, в общем доходе всех олигархов доход $x$ наиболее бедных из них составляет
$$y = \frac{Y(0,9 + 0,1x) − Y(0,9)}{1 − Y(0,9)} = \frac{0,18x + 0,01x^2}{0,19} = \frac{18}{19}x + \frac{1}{19}x^2$$
Это и есть искомое уравнение кривой Лоренца.
Сравнить степень неравенства можно двумя способами.
Способ 1. (Не требует расчета коэффициентов Джини.)
Заметим, что полученная кривая Лоренца лежит ближе к линии абсолютного равенства, чем кривая Лоренца для всей страны: действительно, $\frac{18}{19}x + \frac{1}{19}x^2 > x^2$ для $x ∈ (0; 1)$, так как в этом интервале $x > x^2$. (На Рис. 4.1a новая кривая Лоренца почти неотличима от прямой линии.) Значит, коэффициент Джини распределения доходов среди олигархов меньше, чем коэффициент Джини для всей страны. Среди олигархов степень неравенства доходов меньше, чем в стране в целом.
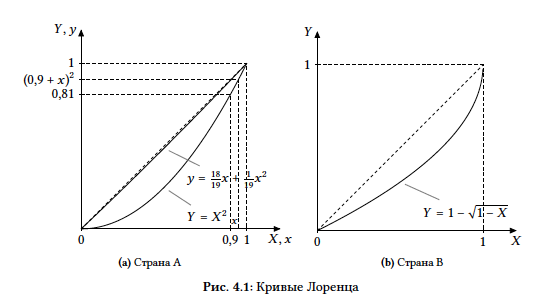
- Действуя по аналогии, получаем, что искомая кривая Лоренца будет иметь вид
$$y = \frac{Y(0,9 + 0,1x) − Y(0,9)}{1 − Y(0,9)} =
\frac{1 − \sqrt{1 − 0,9 − 0,1x} − (1 − \sqrt{1 − 0,9})}{1 − (1 − \sqrt{1 − 0,9})} =\frac{\sqrt{0,1} − \sqrt{0,1 − 0,1x}}{\sqrt{0,1}} = 1 − \sqrt{1 − x}$$
Таким образом, кривая Лоренца распределения доходов среди $10 \%$ богатейших имеет точно такой же вид, как кривая Лоренца в стране в целом! Следовательно, коэффициент Джини распределения доходов среди олигархов точно такой же, как в стране в целом.
Примечание. Для ответа на вопрос не понадобилось рассчитывать сам коэффициент Джини (он равен $1/3$). - Представим себе страну $C$, населенную только олигархами страны $B$. $1$% богатейших жителей страны $B$ являются $10$% богатейших жителей страны $C$ (то есть олигархами среди олигархов). Таким образом, нам нужно сравнить неравенство доходов в стране $С$ в целом и неравенство доходов среди олигархов страны $C$.
В пункте 2 мы решили точно такую же задачу для страны $B$; при этом мы вывели, что в стране $C$ кривая Лоренца имеет точно такой же вид как в стране $B$. Значит, и ответ будет таким же: кривая Лоренца среди олигархов страны $C$ будет иметь такой же вид, как в стране $С$ в целом, и коэффициент Джини будет тем же самым. Продолжая по аналогии, получаем, что и среди $0,1$% богатейших жителей страны $B$ ($1$% богатейших жителей страны $C$) коэффициент Джини будет точно таким же.
Способ 2. Рассчитаем коэффициенты Джини. Во всей стране коэффициент Джини равен
$$\left(\frac{1}{2} - \int_{0}^{1}X^2dX\right) : \frac{1}{2} = 1 - 2\int_{0}^{1}X^2dX = 1 - 2\left(\frac{1^3}{3} - \frac{0^3}{3}\right) = 1 - \frac{2}{3} = \frac{1}{3}$$.
Среди олигархов кoэффициент Джини равен
$$\left(\frac{1}{2} - \int_{0}^{1}\left(\frac{18}{19}x + \frac{1}{19}x^2\right)dx\right) : \frac{1}{2} = 1 - 2\int_{0}^{1}\left(\frac{18}{19}x + \frac{1}{19}x^2\right)dx = 1 - 2\left(\frac{18}{19} \cdot \frac{1}{2} + \frac{1}{19} \cdot \frac{1}{3}\right) = \frac{1}{57}$$
Поскольку $\frac{1}{57}<\frac{1}{3}$, среди олигархов степень неравенства доходов меньше.