а). Выведем изначальный рыночный спрос на велосипеды:
\[Q^D=\begin{cases}114-9p, & \text{если } p\lt 10 \\ 64-4p, & \text{если } 10 \leq p\leq 16 \\ 0, & \text{если } p \gt 16 \end{cases}\]
Пусть в изначальном равновесии установилась цена $P$ (так как первая группа не покупает, то мы знаем что $P \geq 10$), и равновесное количество $Q=64-4P$.
После введения субсидии для первой группы, рыночный спрос стал:
\[Q_{new}^D=\begin{cases}124-9p, & \text{если } p\lt 12 \\ 64-4p, & \text{если } 12 \leq p\leq 16 \\ 0, & \text{если } p \gt 16 \end{cases}\]
Так как теперь покупают обе группы потребителей, а цена и равновесное количество увеличились на 1, то из системы уравнений находим равновесные параметры для обоих случаев:
\[\begin{equation}\begin{cases}Q=64-4P\\ Q+1=124-9(P+1)\end{cases}\\
P=10,Q=24;P+1=11,Q+1=25\end{equation}\]
Пусть функция спроса описывается уравнением $Q^S=a+bp$. Тогда подставляя равновесные параметры в двух случаях, находим $a$ и $b$:
\[\begin{equation}\begin{cases}24=a+10b\\ 25=a+11b\end{cases}\\
a=14,b=1 \rightarrow Q^S=14+p\end{equation}\]
б). Заметим, что в предыдущем случае после введения субсидии потребители с низким спросом покупали 5 единиц. Если субсидия вводится для всех покупателей, то рыночный спрос станет
\[Q_{new}^D=\begin{cases}132-9p, & \text{если } p\lt 12 \\ 72-4p, & \text{если } 12 \leq p\leq 18 \\ 0, & \text{если } p \gt 18 \end{cases}\]
В пересечении с функций предложения получаем $p=11,8$. При такой цене потребители с низким спросом покупают только 1 единицу — меньше, чем раньше. Это объясняется тем, что повышение спроса со стороны второй группы увеличивает равновесную цену, что плохо для покупателей с низким спросом и заставляет их потреблять меньше.

Шпунтик&Со устанавливает цену на шпунтики, которую Винтик&Со воспринимает, как средние переменные издержки производства каждого винтика. Винтик&Со в свою очередь устанавливает цену на винтики, максимизируя свою прибыль:
$$\pi_В=(360-x)(x-y)=-x^2+x(y+360)-360y$$
Вершина параболы по формуле $-b/2a$ определяет максимум:
$$x=\frac{y+360}{2}$$
По такой цене будет произведено и куплено: $Q=\dfrac{360-y}{2}$ винтиков.
Для фирмы Шпунтик&Co это уравнение задаёт спрос на её продукцию. Фирма также устанавливает цену y максимизируя свою прибыль:
$$\pi_Ш=(y-40)\cdot \frac{360-y}{2}=-0.5y^2+200y-7200$$
По формуле вершины параболы однозначно определяется $y$ для достижения максимума прибыли:
$$y=200 \rightarrow x=280$$

а). Введение натурального сбора, уплачиваемого производителями, изменит функцию рыночного предложения, следовательно, изменится цена и решение каждого производителя об объёмах производства.
При любой цене производитель определяет объём производства так, чтобы максимизировать прибыль. Если каждый мастер производит $q$ пар сапог, то продает он $q-(q-1)\cdot0,5$ пары. Тогда:
\[\begin{equation}\pi=P\left(q-(q-1)\cdot0,5\right)-2q^2-4q-10\rightarrow \max\\
0,5P-4=4q\\
q^*=\frac{0,5P-4}{4}=\frac{1}{8} P-1\end{equation}\]
Однако в данной ситуации объём производства не совпадает с объёмом предложения. На рынке каждый мастер будет предлагать $q_s=q^*-(q^*-1)\cdot0,5$. То есть:
\[\begin{equation}q_s=\left(\dfrac{1}{8} P-1\right)-\left(\dfrac{1}{8} P-1-1\right)\cdot0,5\\
q_s=\dfrac{1}{16} P\\
Q_S=40\cdot \dfrac{1}{16} P=2,5P\end{equation}\]
Найдем равновесную цену, равновесное количество и величину предложения одной фирмы:
\[\begin{equation}600-10P=2,5P\\
P=48\\
Q=120\\
q=3\end{equation}\]
То есть на рынке каждый мастер будет продавать 3 пары сапог, а производить: $q^*=\dfrac{1}{8}\cdot48-1=5$
Значит, в виде налога каждым мастером будет уплачено 2 пары сапог $\left(5 – 3 = 2 \text{, или иначе } (5 – 1) \cdot 0,5 = 2\right)$. Следовательно, можно будет обуть 80 дружинников $(40 \cdot2 = 80)$.

б) Прибыль каждого мастера после введения натурального налога:
\[\pi_1=48\cdot3-2\cdot5^2-4\cdot5-10=64\]
Определим объем производства каждого мастера и его прибыль до введения налога. Для этого определим функцию рыночного предложения и равновесную цену.
Предложение каждого мастера определяется из условия $P=MC$:
\[\begin{equation}P=4q+4\\
q_S=\dfrac{P-4}{4}\\
Q_S=10P-40\\
600-10P=10P-40\\
P=32\\
Q=280\\
q=7\\
\pi_0=7\cdot32-2\cdot7^2-4\cdot7-10=88\end{equation}\]

а) Если фирма решит произвести Q единиц товара, ей придется арендовать $\left[Q/30\right]$ станков, каждый стоимостью 120. Кроме того, на каждую из единиц остальные расходы составят $1\cdot3+2\cdot2+3\cdot1+1\cdot1=11$ (заметим, что расходы на электроэнергию зависят непосредственно от числа произведенных единиц.) Таким образом, функция издержек имеет вид: $TC(Q)=11Q+120\left[Q/30\right]$.

б) Заметим, что если станок уже арендован, его выгодно загружать полностью, так как цена больше, чем дополнительные издержки на единицу: $12>11$. Таким образом, станок приносит выгоду в размере $(12-11)\cdot30=30$ тыс. д.е. Издержки же на аренду станка равны $120$ тыс. д.е., и поэтому в отсутствие субсидии фирма не будет открывать производство.

Если государство предложит субсидию в размере $S$ за открытие производства, фирма в любом случае не будет арендовать больше одного станка, так как каждый последующий станок будет приносить лишь убыток, не изменяя величину субсидии.

Таким образом, мининимальная субсидия должна покрыть убытки от аренды одного станка, то есть $120-30=90$. При этой величине субсидии фирма арендует один станок и произведет $30$ тыс. ед.

Разберём три возможных случая выбора мистером Фейнманом места для магазина.

Магазин на заводе A

Рассчитаем предельные издержки (с учётом доставки) продукции, привезённой из разных мест:
$$MC_A=0,5q_A, MC_S=10, MC_B=5q_B+20$$
Фейнман никогда не захочет продавать больше 10 единиц продукции, так как с $Q=10$ начинается неэластичный участок функции спроса, где выручка убывает, то есть прибыль монополиста не может быть максимальна. При этом видно, что даже если произвести 10 единиц продукции на заводе A, предельные издержки производства последней единицы окажутся меньше, чем предельные издержки производства любой единицы в любом другом месте. Следовательно, всё производство будет организовано там же, где находится магазин, и общая функция издержек составит $TC=0,25Q^2$. Функция прибыли в этом случае имеет вид: $$\pi=(20-Q)Q-0,25Q^2$$

Это парабола с ветвями вниз, максимум ее достигается при $Q^*=8$. Подставляя это значение в функцию прибыли, получаем $\pi^*=80$.
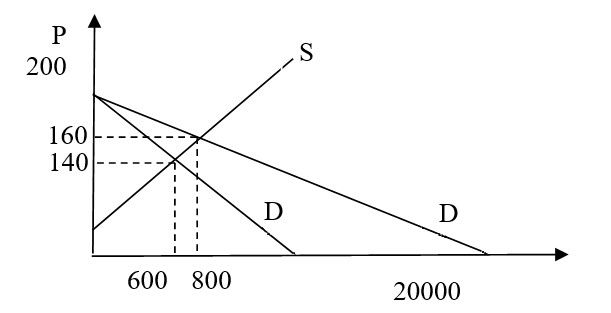
Ситуация изображена на рис. 1.1(a) (заштрихованная площадь соответствует максимальной прибыли).

Магазин на складе

Рассчитаем предельные издержки (с учётом доставки) продукции, привезённой из разных мест:
$$MC_A=0,5q_A+10 ,MC_S=0, MC_B=5q_B+10$$
Ясно, что в первую очередь нужно продать все 5 единиц, находящиеся на складе. При этом $MR(5)=10$, то есть продажа любого количества продукции, превышающего 5, будет приносить меньше 10 долларов предельного дохода в расчёте на дополнительную единицу. Доставка продукции с любого из заводов стоит 10 за единицу (а ещё есть издержки производства), поэтому продавать произведенные на заводах единицы продукции невыгодно. Продав 5 единиц, Фейнман получит прибыль, равную $\pi^*=5\cdot15=75$.
Ситуация изображена на рис. 1.1(b).

Магазин на заводе B

Рассчитаем предельные издержки (с учётом доставки) продукции, привезённой из разных мест:
$$MC_A=0,5q_A+20, MC_S=10, MC_B=5q_B$$
Предельные издержки (включая доставку) даже для самых первых единиц продукции на заводе A больше 20. При этом, используя завод B и продукцию со склада, можно произвести 9 единиц продукции с предельными издержками, не превышающими 20 (5 со склада и 4 на заводе), но даже при 9 единицах продукции предельный доход уже существенно меньше предельных издержек; следовательно, в этом случае завод A использоваться не будет. Сравнивая предельные издержки на доставку со склада и производство на заводе B, можно заметить, что производство на заводе дешевле при первых 2 единицах $(10>5q_b \Leftrightarrow q_b<2)$, затем дешевле брать продукцию со склада, но там находится только 5 единиц, поэтому, если мы хотим производить $Q>7$, придётся вернуться на завод и производить там $(Q-5)$ единиц продукции. Таким образом, функция предельных издержек имеет вид:
$$MC=\begin{cases}5Q, & \text{если } Q \leq 2; \\ 10, & \text{если } 2 \leq Q \leq 7; \\ 5(Q-5), & \text{если } Q \geq 7.\end{cases}$$
Функция предельной выручки имеет вид $MR=20-2Q$ (убывающая функция) и пересекает неубывающую функцию предельных издержек при $Q=5$. Значит, фирма произведет на втором заводе 2 барабана, потратит на это 10 долларов, а еще 3 единицы привезет со склада, потратив на это 30 долларов. Выручка от продажи 5 единиц продукции составит 75, то есть прибыль мистера Фейнмана будет равна $\pi^*=35$.
Ситуация изображена на рис. 1.1(c).

Сравнение вариантов

Получается, то максимальная прибыль $\pi^*=80$ достигается при открытии магазина на заводе A и продаже на нём 8 произведенных там же барабанов.

а) Рассмотрим рекомендацию молодого советника (натуральный налог на покупателей). При рассуждениях о том, как работает этот налог, прадоподобыми будут выглядеть две версии:

Версия 1: спрос вырастет, потому что покупателям нужно отдавать половину купленного, так что они будут покупать больше, чтобы что-то осталось для потребления.
Версия 2: спрос упадёт, потому что потребители не хотят покупать для государства — действительно, зачем покупать, если кто-то заберёт купленное?

На самом деле, действуют оба эффекта, и при разных ценах доминирует или первый, или второй:

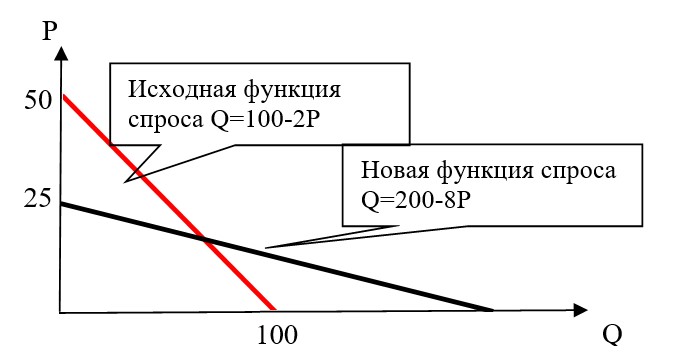
Как получается новая функция спроса? Попробуем воспроизвести рассуждения типичного покупателя.

• Чтобы съесть $Q$, нужно купить $2Q$ и потратить $2PQ$, то есть $2P$ на каждую съеденную единицу.
• Значит, фактически, если на ценнике написано $P$, я плачу $2P$ — именно такую цену нужно подставить в старый спрос.
• $100-2(2P)$ — спрос на съеденные единицы.
• Однако к предложению нужно приравнивать не количество съеденных единиц, а количество купленных. Их вдвое больше: $D=200-8P$.
• Равновесие: $200-8P=2P-20 \Leftrightarrow P^*=22,Q^*=24,T=12$.

б) Рассуждая про производителей аналогично, можем получить новую функцию предложения:

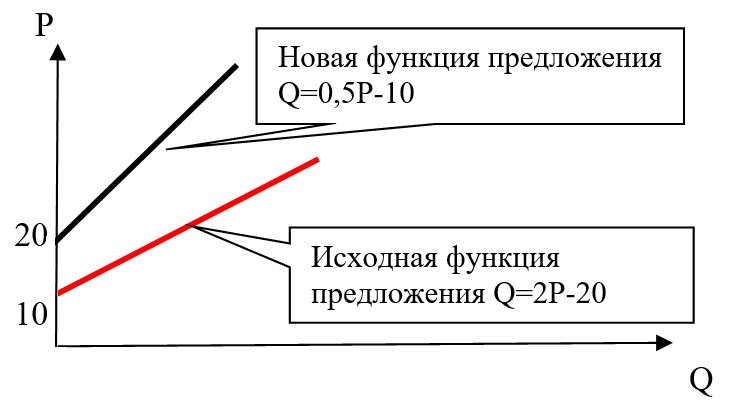
Рассуждения типичного производителя:

• Если произведем $Q$, то продадим $Q/2$. Выручка составит $PQ/2$, то есть $P/2$ на каждую произведённую единицу — именно эта цена волнует продавца, её и надо подставлять в предложение.
• $2P-20$ — предложение произведённых единиц.
• Но к спросу нужно приравнивать не то, что производится, а то, что продаётся: вдвое меньше: $S=P-10$.
• Отсюда $100-2P=P-10 \Leftrightarrow P^*=44,Q^*=12,T=12$.

в) Получилось, что разницы между налогами с точки зрения сборов нет. Однако есть ли разница на практике? Возможен такой аргумент. Производителей, как правило, меньше, чем потребителей, а значит, совокупные транзакционные издержки, связанные с уплатой налогов, будут меньше. Производители привыкли отчитываться (с помощью кассовых аппаратов) о каждой операции, так что ввести налог на них будет меньшим бременем, чем на потребителей. Возможны и другие идеи.

Математическая основа задачи заимствована из пособия: Белоносов В.С., Фокин М.В. Задачи вступительных экзаменов по математике: Учеб. пособие. Новосибирск: Сиб. унив. изд-во, 2005.
Обозначим через $X$, $Y$ и $Z$ численность волшебников с высшим, средним и начальным образованием, соответственно. Пусть до кризиса в городе $N$ проживали $X_0$, $Y_0$ и $Z_0$ волшебников, уехали соответственно $X_1$, $Y_1$ и $Z_1$, а осталось $X_2$, $Y_2$ и $Z_2$ волшебников.

Удобно информацию из условия записать в таблицу:

Уровень образования волшебника	Жили в городе $N$ до кризиса	Уехали из города $N$	Остались в городе $N$
высшее	$X_0=0,45\cdot M=\dfrac{9}{20}\cdot M$	$X_1$	$X_2=(X_0–X_1) \leq 40$
среднее	$Y_0=0,3\cdot M=\dfrac{3}{10}\cdot M$	$Y_1$	$Y_2=Y_0-Y_1$
начальное	$Z_0=0,25\cdot M=\dfrac{1}{4}\cdot M$	$\begin{array} ZZ_1=1,2\cdot Y_1=\dfrac{6}{5}\cdot Y_1 \\ Z_1=0,6\cdot X_1=\dfrac{3}{5}\cdot X_1\\ \text{ или } Y_1=\dfrac{1}{2}\cdot X_1\end{array}$	$Z_2=\dfrac{1}{4}\cdot Z_0=\dfrac{1}{4}\cdot \left(\dfrac{1}{4}M\right)$

Так как число волшебников в любом случае может быть только целым числом, то $M$ можно представить как $20\cdot n$, или $4\cdot5\cdot n$, где $n$ – это натуральное число. В этом случае $X_0$, $Y_0$ и $Z_0$ будут целыми числами.

Число оставшихся в городе волшебников с начальным образованием $Z_2$ тоже должно быть целым числом, а это значит, что $n$ следует представить как $4\cdot k$, где $k$ – это натуральное число. Получаем, что $M=4\cdot5\cdot4\cdot k$, а $Z_2=5\cdot k$. А так как $Z_1$ в 3 раза больше $Z_2$, то получаем, что $Z_1=3\cdot5\cdot k$.

Теперь мы можем выразить $X_1$. Итак, $X_1=5\cdot5\cdot k$, т.е. оно тоже целое.

Конечно, $Y_1$ тоже должно быть целым, следовательно, мы должны представить $k$, как $2\cdot a$, где $a$ – это тоже натуральное число.

Теперь рассчитаем $X_2$. В наших обозначениях $X_0=9\cdot4\cdot2\cdot a$. $X_1=5\cdot5\cdot2\cdot a$. Получаем $X_2=a\cdot(9\cdot4\cdot2–5\cdot5\cdot2)=a\cdot(72–50)=a\cdot22$. Но по условию $X_2 \leq 40$, т.е. $a\cdot22\leq40$. А так как $a$ – это натуральное число, то оно может принимать здесь только одно значение $a=1$.

В итоге мы получаем, что $M=4\cdot5\cdot4\cdot2\cdot1=160$. То есть до кризиса в городе проживало 160 волшебников.

б) Суммарный рыночный спрос – это сумма индивидуальных спросов. Сначала разберемся с групповыми функциями спроса волшебников:

1. Волшебники с высшим образованием. До кризиса их численность в городе $N$ составляла $0,45\cdot160=72$ человека. Значит их суммарный спрос будет равен $Q_x=72\cdot(10–2P)=720–144P$. И они предъявляли спрос на волшебное зелье при цене ниже 5 рубликов.
2. Волшебники со средним образованием. До кризиса их численность в городе $N$ составляла $0,3\cdot160=48$ человек. Значит, их суммарный спрос будет равен $Q_y=48\cdot(30–3P)=1440–144P$. И они предъявляли спрос на волшебное зелье при цене ниже 10 рубликов.
3. Волшебники с начальным образованием. До кризиса их численность в городе $N$ составляла $0,25\cdot160=40$ человек. Значит, их суммарный спрос будет равен $Q_z=40\cdot(60–4P)=2400–160P$. И они предъявляли спрос на волшебное зелье при цене ниже 15 рубликов.

Получаем, что при цене ниже 5 рубликов за литр, спрос на волшебное зелье предъявляли все волшебники, при цене от 5 до 10 рубликов – только волшебники со средним и начальным образованием, а при цене от 10 до 15 рубликов уже только волшебники с начальным образованием.
Функция суммарного рыночного спроса будет иметь вид:
$$Q=\begin{cases} 0, & \text{при } 15 \leq P; \\ 2400-160P, & \text{при } 10 \leq P \leq 15; \\ 3840-304P, & \text{при } 5 \leq P \leq 10; \\ 4560-448P, & \text{при } 0\leq P \leq 5\end{cases}$$

а) Стоимость одной порции салата составит для Юного экономиста $20+10k$ д.e., а значит, он сможет потребить $\dfrac{1000}{20+10k}$ порций. Полезность от каждой порции равна $\sqrt{k}$, а значит итоговая полезность ЮЭ будет равна: $$U(k)=\frac{100\sqrt{k}}{2+k}$$
Нам нужно найти значение $k\in [1/4;4]$, при котором значение этого выражения максимально. Это можно сделать стандартным методом — с помощью производной. Есть и решение, не требующее знания производной: разделим числитель и знаменатель на $\sqrt{k}$: $$U(k)=\frac{100}{\sqrt{k}+2/\sqrt{k}}$$
Значение дроби максимально, когда знаменатель минимален. Заметим, однако, что $\sqrt{k}+2/\sqrt{k}=\left(\sqrt[4]{k}-\sqrt{2}/\sqrt[4]{k} \right)^2+2\sqrt{2}$. Поэтому знаменатель минимален тогда и только когда, когда $\sqrt[4]{k}-\sqrt{2}/\sqrt[4]{k}=0$, то есть $k=2$. (Этот же результат можно было получить с помощью неравенства между средним арифметическим и средним геометрическим)

б) Первый способ

Общие затраты на оба типа порций будут равны $(20+10k_1)\cdot x_1+(20+10k_2)\cdot x_2=1000$. Общая полезность: $$U=x_1 \sqrt{k_1}+x_2\sqrt{k_2}$$
Пусть $x_1$ и $k_1$ выбраны на каких-то произвольных (необязательно оптимальных) уровнях. Тогда $U=const_1+x_2\sqrt{k_2}$, а расходы равны $const_2+(2+k_2)\cdot x_2=100$. Отсюда
$$U=const_1+\frac{100-const_2}{2+k_2}\sqrt{k_2}$$
Максимизируя эту функцию (она с точности до констант похожа на функцию в пункте а) получаем, что $k_2^*=2$ независимо от $k_1$. Аналогично $k_1^*=k_2^*=2$ — ЮЭ не сможет получить больше полезности, так как он не будет пользоваться возможностью делать разные салаты.

Второй способ
Докажем, что ЮЭ не может получить полезность больше, чем в а), то есть больше, чем $25\sqrt{2}$. Назовем «порциями первого типа» те, в которых пропорция помидоры: огурцы равна $k_1$, а «порциями второго типа» те, в которых пропорция равна $k_2$. Пусть ЮЭ готовит $x_1$ порций первого типа и $x_2$ порций второго типа. Обозначим его расходы на порции первого типа за $E_1$, а расходы на порции второго типа — за $E_2$.
Полезность ЮЭ равна $$U=x_1\sqrt{k_1}+x_2\sqrt{k_2}=\frac{E_1}{20+10k_1}\sqrt{k_1}+\frac{E_2}{20+10k_2}\sqrt{k_2}$$
Заметим, однако, что из пункта а) мгновенно следует, что $\dfrac{\sqrt{k_1}}{20+10k_1}=\dfrac{\sqrt{2}}{40}$ и $\dfrac{\sqrt{k_2}}{20+10k_2}=\dfrac{\sqrt{2}}{40}$. Поэтому
$$U=„\frac{\sqrt{2}}{40} E_1+\frac{\sqrt{2}}{40} E_2=\frac{\sqrt{2}}{40}\cdot(E_1+E_2)=\frac{\sqrt{2}}{40}\cdot 1000=25\sqrt{2}$$
что и требовалось доказать.

Уменьшение спроса на фуа-гра должно уменьшить расходы на покупку этого деликатеса, и эта экономия бюджета, как следует из условия, будет потрачена на сыр. Найдем расходы на фуа-гра до и после кампании в СМИ.

Известно, что до кампании цена банки фуа-гра составляла 160 юаней. Очевидно, это цена соответствует изначальному равновесию. Равновесное количество товара на рынке (рассчитанное как величина спроса) составляет $40000-200\cdot160=8000 \text{ банок}$. Таким образом, расходы на фуа-гра до компании составляли $8000\cdot160 = 1\text{ млн } 280 \text{ тыс. юаней}$.

Про предложение известно, что его функция линейная (100 банок дополнительно при росте цены на 1 юань), и этой функции принадлежит точка исходного равновесия $(160;8000)$. Поставщики не будут продавать фуа-гра при цене ниже 80 юаней (цена должна упасть до 80 юаней, чтобы величина предложения стала равной 0). Таким образом, функция предложения (и по условию задачи она не изменится) равна: $Q_s=100p-8000$.

Графики функций предложения и спроса до и после кампании о жестоком обращении с гусями представлены на рисунке:

Новая функция спроса $Q_D=20000-100p$

Найдём новое равновесие и расходы на фуа-гра после кампании в СМИ.
$Q_D=20000-100p=100p-8000= Q_s$, откуда находим $Р=140$ юаней, равновесное количество – $6000$ банок фуагра. Расходы гурманов на фу-гра теперь составляют $6000\cdot140=840$ тыс. юаней.

Экономия гурманских бюджетов в Гуанчжоу после кампании составила $1280000-840000=440000$ юаней. На эту сумму можно купить дополнительно 2750 головок сыра реблюшон.

Так как плащи будут изготавливаться на тех же станках, что и скатерти, и станки эти полдня простаивают, то подписание договора не увеличит постоянные издержки. Возрастут только переменные издержки на $100\cdot10 = 1000$ монет (зарплата мастериц за полдня). Кроме того, возрастут неявные переменные издержки на $100\cdot5 = 500 $ (такую сумму можно было бы выручить за продажу невидимых нитей, если бы они не понадобились для изготовления плащей). Итого экономические издержки возрастут на 1500 монет. Доход же мастерской увеличится на $100\cdot16 = 1600$ монет. Таким образом, экономическая прибыль увеличится на 100 монет в месяц. Поэтому договор следует подписать.

Расходы на оплату консультанта являются безвозвратными издержками и при принятии решений о будущем не учитываются.

а) Себестоимость изготовления одного стола равна:
$0,5\cdot410+5\cdot220+150+100+5=1560 \text{ рублей}$

б) $\text{Цена} = \text{себестоимость} + \text{прибыль}$

Прибыль в расчёте на один стол равна $1560\cdot0,4=624 \text{ рубля}$. Следовательно, цена стола равна $2184$ рубля.

а). Для начала нужно определить, кто из стоматологов имеет сравнительное преимущество в выполнении работы медицинской сестры, а кто в лечении больных. Для удобства занесем всю необходимую информацию в таблицу:

Стоматологи	Количество обслуженных больных	Условные часы работы медицинской сестры	Альтернативная стоимость 1 условного часа работы медицинской сестры	Альтернативная стоимость лечения 1-го больного	Специализация в соответствии со сравнительными преимуществами
Иван	6	6	1 больной	1 час работы медсестры	работа медицинской сестры
Антон	9	4	$9/4=2,25$ больных	$4/9\approx0,44$ часа работы медсестры	лечение больных
Михаил	10	5	2 больных	0,5 часа работы медсестры
ВСЕГО	25	15

Определив сравнительные преимущества стоматологов, мы построим КПВ будущей клиники.

б). Если нужно выполнить всю работу медицинской сестры, то в первую очередь этой работой займется Иван, так как он имеет в этом деле сравнительные преимущества. Но за рабочий день он сможет выполнить только часть работы (оценивается в 6 условных часов), а значит, ему должен помочь Михаил, так как у него альтернативная стоимость 1 часа работы медсестры меньше, чем у Антона. Однако он будет заниматься этой работой не полный день, а ровно столько, сколько требуется для выполнения работы, оцениваемой в 4 условных часа работы медсестры. За оставшееся время он сможет принять $(10-4\cdot2)=2$ больных. Антон же весь день будет лечить больных. Соответственно всего за день можно будет принять $9+2=11$ больных. По условию этого недостаточно для обеспечения прибыльности бизнеса, так как в день клиника должна принимать не менее 20 больных.

в). Если стоматологи наймут медицинскую сестру, которая может выполнять только сестринскую работу, но не может лечить больных, то КПВ клиники примет вид:

г). Медицинская сестра за свой рабочий день (8 часов) может выполнить 8 часов работы медсестры, следовательно, стоматологам дополнительно придётся выполнять всего 2 часа работы медицинской сестры. По прежнему эту работу лучше всего поручить Ивану, так как у него альтернативная стоимость выполнения этой работы наименьшая. Выполнив работу медсестры, за оставшееся время он сможет принять $(6-2\cdot1)=4$ больных. Антон и Михаил при этом весь день будут лечить больных. Всего клиника за день сможет принять $(9+10+4)=23$ больных.

Без привлечения обслуживающего персонала клиника могла в день лечить только 11 больных, теперь же она может принять 23 больных. Дополнительный доход, в данном случае под доходом понимается выручка, составит $(23-11)\cdot1300=15600$ рублей.