1. Полдники

В любой стране для приготовления 1 пирожка необходимы 2 единицы муки ($x$) и 1 единица капусты ($y$), для приготовления стакана морса нужна только 1 единица смородины ($z$). Уравнения, описывающие кривые производственных возможностей относительно ресурсов, представлены в таблице. Найдите максимальное общее количество полдников, которое можно приготовить в двух странах, если:
а) (7 баллов) обмен между странами невозможен;
б) (8 баллов) страны могут обмениваться пирожками и морсом;
в) (15 баллов) страны могут обмениваться пирожками, морсом и капустой.
Аналогично, $P_{б}$ и $M_{б}$ — объемы производства пирожков и морса в Бэриленде. Снова имеем соотношения $x_{б}=2P_{б}$, $y_{к}=P_{б}$, $z_{б}=M_{б}$, откуда получаем, что $4P_{б}+M_{б}=120$. Вновь учитывая, что $P_{б}=M_{б}$, получаем, что $P_{б}=M_{б}=24$.
Таким образом, максимальный мировой объем потребления полдников равен $30+24=54$ полдника.
Примечание. Участник может не выводить КПВ относительно товаров, а сразу перейти к уравнениям, учитывающим пропорции необходимых ресурсов: например, $2z_{к}+z_{к}+z_{к}=120$ и $2z_{б}+2z_{б}+z_{б}=120$. При корректном обосновании этого способа действия баллы не должны снижаться.
Кривые производственных возможностей относительно товаров:
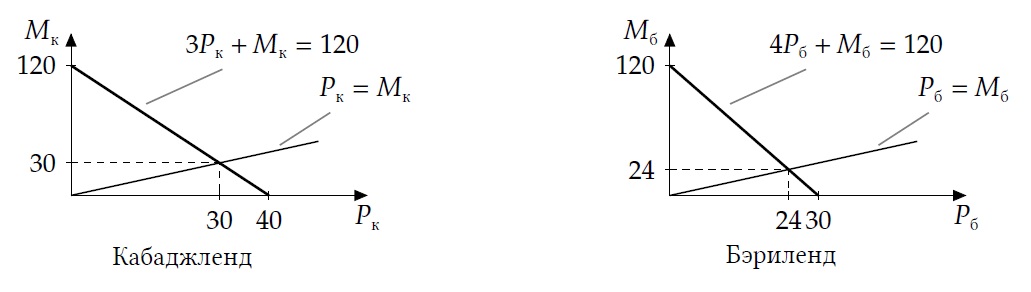
б) (8 баллов) В пункте (а) мы вывели, что уравнения КПВ стран в координатах <<пирожки-морс>> имеют вид $3P_{к}+M_{к}=120$ и $4P_{б}+M_{б}=120$. Сложим эти КПВ стандартным образом:
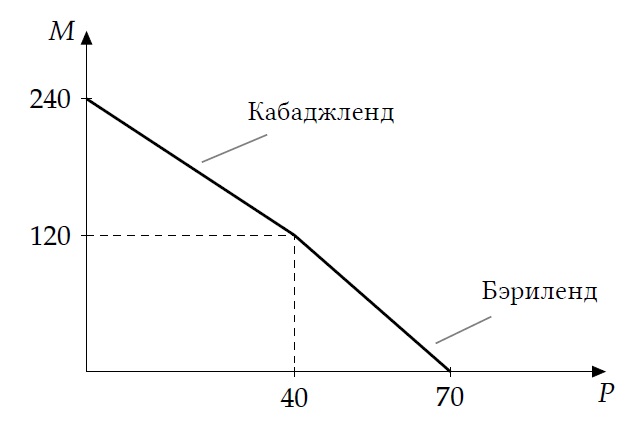
Уравнение этой КПВ имеет вид:
$$M=
\begin{cases}
240-3P, \text{ если } P<40;\\
280-4P, \text{ если } 40\leqslant P\leqslant 70,
\end{cases}$$
где $P$ и $M$ — мировые объемы производства пирожков и морса соответственно.
Теперь нам нужно пересечь график мировой КПВ с лучом $P=M$
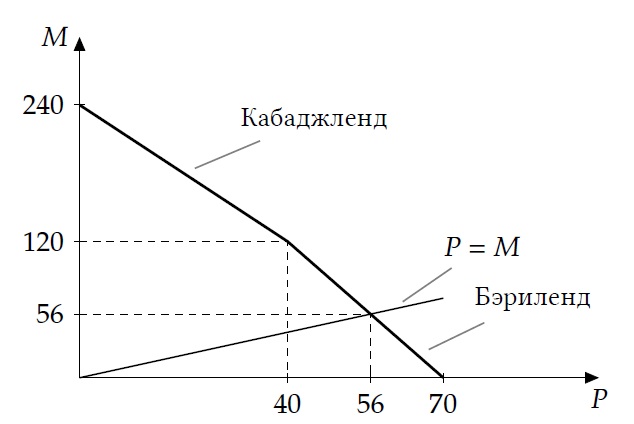
Заметим, что точка излома КПВ имеет координаты $(40, 120)$, то есть в ней $M>P$. Следовательно, пересечение в КПВ произойдет на втором участке, то есть тогда, когда $M=280-4P$. Получаем уравнение $M=280-4M$, откуда $M=P=56$.
Таким образом, максимальный мировой объем потребления полдников теперь равен 56.
Примечание. Задача может быть решена и без получения уравнения суммарной КПВ. Воспользовавшись идеей о сравнительных преимуществах (альтернативная стоимость пирожка в Кабаджленде меньше, чем в Бэриленде), заметим, что первый пирожок должен быть произведен в Кабаджленде. Однако даже если мы произведем там все возможные пирожки (40 штук), морса в Бэриленде можно будет произвести большее количество (120 стаканов), значит, там тоже частично нужно производить пирожки. Производя $x$ дополнительных пирожков, мы отказываемся в Бэриленде от $4x$ стаканов морса. Чтобы в сумме не было лишних пирожков или морса, должно быть выполнено $40+x=120-4x$, то есть $x=16$ и всего можно произвести 56 полдников.
в) (15 баллов) Докажем, что максимальный мировой объем потребления полдников равен 60. Для этого: 1) докажем, что искомый объем потребления не больше 60 (оценка); 2) приведем пример обмена между странами, при котором искомый объем равен 60 (пример).
1) (Оценка) Выпишем снова уравнения КПВ стран относительно ресурсов:
$$\begin{cases}
x_{к}+y_{к}+z_{к}&=120,\\
x_{б}+2y_{б}+z_{б}&=120.
\end{cases}$$
Сложим эти уравнения (просто как уравнения, а не в смысле сложения КПВ). Получаем
$$(x_{к}+x_{б})+(y_{к}+y_{б})+(z_{к}+z_{б})=240-y_{б}$$
Обозначим количество полдников за $Q$. Заметим, что, в силу пропорций производства и потребления верны следующие равенства: $2Q=x_{к}+x_{б}$, $Q=y_{к}+y_{б}$, $Q=z_{к}+z_{б}$. Подставляя эти равенства в уравнения выше, получаем, что
$$2Q+Q+Q=240-y_{б}\leqslant 240$$
Таким образом, $4Q\leqslant 240$, откуда $Q\leqslant 60$, что мы и хотели доказать.
2) (Пример.) 60 полдников страны могут получить следующим образом:
- Кабаджлэнд производит 60 единиц муки и 60 единиц капусты;
- Берилэнд производит 60 единиц муки и 60 единиц смородины;
- Кабаджлэнд отправляет 30 единиц капусты в Бэриленд, где из муки и этой капусты делают 30 пирожков;
- Из оставшейся капусты и муки в Кабаджлэнде делают 30 пирожков.
- Из смородины в Бэрилэнде делают 60 единиц морса;
- Бэрилэнд отправляет в Кабаджлэнд 30 единиц морса, в результате чего в каждой стране оказывается по 30 полдников.
Примечание 1. Этот пример не единственен. Легко проверить, что подойдет любой пример, в котором Кабаджлэнд производит 60 единиц капусты и отправляет в Бэрилэнд не меньше 30 из них (и при этом производство муки в двух странах определяется из количеств капусты, которые окажутся в двух странах в результате этого, а производство смородины определяется по остаточному принципу)
Примечание 2. Построение примера является неотъемлемой частью решения. Из того, что выполнено неравенство $Q\leqslant 60$ еще не следует, что оно может быть выполнено как равенство. Действительно, наше доказательство неравенства $Q\leqslant 60$ никак не учитывало возможности торговли, а потому это неравество могло быть абсолютно так же доказано и в пунктах а) и б). Тем не менее, как мы видим, в этих пунктах верхняя граница $Q=60$ не достигается.
2. Упрощёнка
Рассмотрим подобную систему в рамках простой модели. Представим себе фирму на рынке совершенной конкуренции, функция издержек которой описывается уравнением $TC=0,5q^{2}+10q$, где $q$ — объем выпуска. Государство предлагает фирме на выбор два налога — налог в размере 10% от выручки или в размере 36% от прибыли (эти ставки отличаются от действующих в современной России). При каждой цене $P$ фирма решает, сколько единиц продукции произвести и какой из двух налогов платить. Фирма максимизирует прибыль.
Выведите уравнение функции предложения фирмы. Может ли в данном случае фирма при росте цены снизить выпуск? (Если да, то приведите пример, если нет, то обоснуйте.)
1) Налог на выручку. Фирма будет максимизировать $$\pi_\bigtriangledown(q)=(1-0,1)TR(q)-TC(q)=0,9pq-0,5q^{\,2}-10q.$$ Графиком функции прибыли является парабола с ветвями \linebreak вниз, поэтому оптимальный выпуск находится в ее вершине, если абсцисса вершины неотрицательна, и равен нулю в противном случае: $q=0,9p-10$ при $p\geqslant 100/9$ и $q=0$ при $p< 100/9$. Максимальная прибыль при этом составит
$$\pi_\bigtriangledown(p)=
\begin{cases}
0,&\text{ если } p< 100/9;\\
\dfrac{(0,9p-10)^2}{2},&\text{ если } p \geqslant 100/9.\\
\end{cases}$$
2) Налог на прибыль. Фирма будет максимизировать
$$\pi_\bigtriangleup(q)=(1-0,36)\left(TR(q)-TC(q)\right)=0,64(pq-0,5q^{\,2}-10q).$$ Графиком функции прибыли вновь является парабола с ветвями вниз, поэтому оптимальный выпуск находится в ее вершине, если абсцисса вершины положительна, и равен нулю в противном случае: $q=p-10$ при $p\geqslant 10$ и $q=0$ при $p<10$. Максимальная прибыль при этом составит
$$\pi_\bigtriangleup(p)=
\begin{cases}
0,&\text{ если } p< 10;\\
0,64\dfrac{(p-10)^2}{2},&\text{ если } p \geqslant 10.\\
\end{cases}$$
3) Теперь найдем, при каких ценах выгоднее выбирать налог на выручку, а при каких — налог на прибыль. Выбирать налог на выручку выгоднее, если $\pi_\bigtriangledown(p)>\pi_\bigtriangleup(p)$. Разобьем значения цены на интервалы в соответствии с полученными выше результатами:
- $p\le 10$. В этом случае оптимальный выпуск при двух налогах совпадает и равен 0.
- $10 < p\le 100/9$. В этом случае $\pi_\bigtriangleup(p) > 0$, а $\pi_\bigtriangledown(p)=0$ — лучше выбирать налог на прибыль и производить $q=p-10$.
- $p > 100/9$. В этом случае налог на прибыль выгоднее, если $$0,64\frac{(p-10)^2}{2}>\frac{(0,9p-10)^2}{2}.$$
Это неравенство легко решить, умножая обе части на 2 и извлекая квадратный корень (выражения в скобках положительны). Получаем $p< 20$ — условие, при котором налог на прибыль (и производить $q=p-10$) выгоднее. При $p >20$ выгоднее выбирать налог на выручку (и производить $q=0,9p-10$), при $p=20$ варианты равнозначны.
В итоге, функция предложения фирмы будет описываться уравнением
$$q_s(p)=
\begin{cases}
0,&\text{если } p<10;\\
p-10,&\text{если } 10\leqslant p\leqslant 20;\\
0,9p-10,&\text{если } p\geqslant 20.
\end{cases}$$
(При $p=20$ оба выпуска ($p-10$ и $0,9p-10$) являются оптимальными.)
При росте цены фирма может снизить выпуск. Например, при росте цены с 19 до 21 фирме выгодно снизить выпуск с 9 до 8,9 единиц.
3. Закупка и налог
В 2015 году на этих рынках функции спроса и предложения имели вид:
| Спрос | Предложение | |
| Товар $X$ | $X_D=10/P_X$ | $X_S=10P_X $ |
| Товар $Z$ | $Z_D=40/P_Z$ | $Z_S=10P_Z$ |
В 2016 году правительство страны Альфа планирует закупить 15 единиц товара X для своих нужд. Чтобы сохранить прежнее сальдо бюджета, правительство профинансирует эту закупку за счет потоварного налога, взимаемого с производителей другого товара.
Считайте, что других событий, способных как-то повлиять на спрос и предложение товаров, в 2016 году не произойдет. Иными словами, не будет воздействия никаких прочих факторов, а рынки товаров X и Z не связаны между собой (то есть, например, X не является субститутом или комплементом Z, а также ресурсом для его производства). При расчете ВВП игнорируйте все возможные мультипликативные эффекты.
- (5 баллов) Не проводя расчетов, определите, вызовет ли политика правительства инфляцию или дефляцию в стране Альфа в 2016 году. Аргументируйте свой ответ.
- (10 баллов) Какую ставку потоварного налога на производство товара Z следует установить правительству для выполнения сформулированной задачи?
- (10 баллов) На сколько процентов и в каком направлении в результате указанной политики изменится реальный ВВП страны Альфа? Считайте базовым 2015 год.
- (5 баллов) Чему будет равен индекс потребительских (ИПЦ) в стране Альфа в 2016 году? Примите индекс 2015 года за единицу.
b) В 2016 году за счет государственных закупок товара X спрос на этот товар составит:
$$X_D=\dfrac{10}{P_X}+15$$
Найдём новое равновесие на рынке этого товара:
$$\frac{10}{P_X}+15=10\cdot P_X,
\\ P^{2016}_X=2,\ X^{2016}=20$$
Для закупки 15 единиц товара X по такой равновесной цене государству потребуется $15\cdot 2=30$ денежных единиц, следовательно, потоварный налог на рынке товара Z нужно устанавливать таким образом, чтобы поступления в бюджет в результате его введения равнялись этой сумме.
С учетом налога функция предложения в 2016 году будет иметь вид: $Z_S=10\cdot (P_Z-t)$, а функция спроса останется без изменений. Из всего сказанного выше следует система уравнений, откуда можно найти все нужные нам переменные:
$$\begin{cases}
\dfrac{40}{P_Z}=10\cdot (P_Z-t) \\
\dfrac{40}{P_Z}\cdot t=30
\end{cases}
$$
Решая эту систему, находим:
\[P_Z^{2016}=4,\quad t=3\] Ставка налога составляет 3 денежных единицы.
c) Чтобы найти равновесные параметры двух рынков до государственного вмешательства (в 2015 году), приравняем спрос и предложение из таблицы в условии:
$$\begin{cases}
\dfrac{10}{P_X}&=10P_X \\
\dfrac{40}{P_Z}&=10P_Z
\end{cases}
$$
Решив эту систему, составим таблицу из известных значений цен и выпусков:
$$\begin{array}{|c|c|c|c|c|} \hline & P_X & X & P_Z & Z \\
\hline 2015 & 1 & 10 & 2 & 20 \\
\hline 2016 & 2 & 20 & 4 & 10 \\ \hline \end{array}$$
Реальный ВВП 2015 года равен: $$P^{2015}_X\cdot X^{2015}+P^{2015}_Z\cdot Z^{2015}=1\cdot 10+2\cdot 20=50.$$
Реальный ВВП 2016 года (в ценах 2015 года) равен: $$P^{2015}_X\cdot X^{2016}+P^{2015}_Z\cdot Z^{2016}=1\cdot 20+2\cdot 10=40$$
Таким образом, в результате реализации предложенной политики реальный ВВП упадет на 20%.
г)
$$\text{ИПЦ}=\frac{P^{2016}_X\cdot X^{2015}+P^{2016}_Z\cdot Z^{2015}}{P^{2015}_X\cdot X^{2015}+P^{2015}_Z\cdot Z^{2015}}=\frac{2\cdot 10+4\cdot 20}{50}=2$$
4. Осторожный Кузьма
Кузьма рассматривает возможность вложить деньги в более доходные, но и более рискованные финансовые инструменты. Он может купить акции компании-туроператора A или компании B, продающей зонтики, а также комбинировать эти варианты.
Доходность акций в течение будущего года зависит от погоды, которая неизвестна заранее. Погода может оказаться либо хорошей (и тогда будут пользоваться популярностью услуги туроператора A), либо плохой (и тогда будут пользоваться популярностью зонтики компании B). Текущая стоимость активов, а также ожидаемая Кузьмой стоимость активов в зависимости от погоды представлены в таблице:

Брать кредит Кузьма не может, других способов вложения денег нет. Обозначим за $a$ и $b$ суммы денег (в миллионах рублей), вложенные в акции соответствующих компаний, а за $d$ — сумму, оставшуюся на депозите. Под стоимостью портфеля будем понимать сумму стоимости имеющихся у Кузьмы акций и суммы денег на его счету.
а) (8 баллов) Предположим, что перед тем, как Кузьма должен принять решение о~вложении в активы, Гидрометцентр делает одно из двух предсказаний: «будет хорошая погода» или «будет плохая погода». Как Кузьма поступит со своими деньгами в~зависимости от прогноза (считайте, что он безоговорочно верит этому прогнозу), если он хочет, чтобы стоимость его портфеля через год была максимальной? Чему будет равна ожидаемая стоимость его портфеля через год в каждом из этих случаев?
б) (15 баллов) Предположим, Кузьма должен принять решение до того, как Гидрометцентр сделал прогноз. Для каждого распределения денег между акциями и депозитом он рассчитывает стоимость своего портфеля через год при наименее благоприятной для данного распределения денег погоде. Затем он выбирает такое распределение денег, при котором рассчитанная минимальная стоимость портфеля через год максимальна. Как он распределит деньги в этом случае? (Назовем такую стратегию осторожной.) Чему будет равна стоимость его портфеля через год?
в) (7 баллов) Если бы у Кузьмы была возможность заплатить Гидрометцентру, чтобы получить предсказание погоды до вложения в активы, какую максимальную сумму он был бы готов заплатить? Считайте, что оплата производится до предсказания, а Кузьма придерживается осторожной стратегии как при выборе распределения денег, так и и при принятии решения о том, покупать прогноз погоды или нет.

(Изначальные коэффициенты перед $a$ и $b$ рассчитаны как отношение новой и старой цены, то есть показывают, во сколько раз увеличиваются вложения. Соответствующее количество акций равно $a/10$ и $b/10$, а их стоимость через год, скажем, при хорошей погоде равна $20a/10=2a$ и $7a/10=0,7b$.)
а) Каждая из двух получившихся функций возрастает по одной из переменных ($a$ или $b$) и убывает по другой. Значит, для максимизации нужно выбирать максимально возможное значение одной переменной (1,5) и минимальное значение другой (0). Таким образом, нужно вкладывать в акции определенной компании все 1,5 миллиона, не оставляя ничего на депозите.
К такому же выводу можно было прийти, сравнив доходности трех активов: у депозита она равна 10%, у компании А в хорошую погоду и у компании В в плохую погоду — больше ($100\%$ и $40\%$), а у компании В в хорошую погоду и у компании В в плохую погоду — меньше ($-40\%$ и $-30\%$).
Таким образом, при хорошем прогнозе погоды Кузьма вложит все деньги в акции компании А, а при плохом — вложит все деньги в акции компании В, не оставляя ничего на депозите. (Также ответ можно дать в виде количества акций: нужно купить 150 тыс. акций соответствующей компании.) В первом случае ожидаемая стоимость портфеля через год будет равна 3 млн руб., а во втором она будет равна 2,1 млн руб.
Примечание. Необязательно записывать функции конечной стоимости портфеля именно так, как они записаны выше. В частности, можно выразить из равенства $a+b+d=1,5$ другую переменную и максимизировать функцию по оставшимся, или решать задачу условной максимизации.
б) Найдем, при каком условии стоимость портфеля в хорошую погоду будет не меньше, чем в плохую (то есть минимальной будет стоимость портфеля при плохой погоде):
$$1,65+0,9a-0,4b \ge 1,65-0,5a+0,3b \Leftrightarrow
2a\ge b.$$
Минимальная (из двух типов погоды) стоимость портфеля Кузьмы составит
$$ \min\{S_g; S_b\}=
\begin{cases}
1,65+0,9a-0,4b, & \text{если } 2a\le b;\\
1,65-0,5a+0,3b, & \text{если } 2a\ge b.
\end{cases}$$
Кузьма стремится, чтобы значение этого выражения было максимально, выбирая $a$ и $b$, удовлетворяющие условиям $a\geqslant 0$, $b\geqslant 0$, $a+b\leqslant 1,5$. (Значение $d$ затем определяется автоматически из условия $d=1,5-a-b$.)
Зафиксируем $a$ и найдем оптимальное $b$ при каждом $a$. Как видно из формулы минимальной стоимости портфеля, Кузьме нужно выбирать самое маленькое $b$ при $2a\le b$ и самое большое $b$ при $2a\ge b$. Так или иначе, решением будет $b=2a$, то есть ему нужно сделать так, чтобы стоимость портфеля была одинакова независимо от погоды.
Тогда стоимость активов будет равна
$$S= 1,65+0,9 a-0,4\cdot 2a=1,65+0,1a.$$
Видно, что эта функция возрастает по $a$, то есть оптимальным будет максимальное значение $a$, удовлетворяющие условию $a+2a\leqslant 1,5$, откуда $a=0,5$, $b=2a=1$, $d=0$.
Итак, Кузьма должен вложить 500 тыс. руб. в акции компании A и 1 млн руб. в акции компании B. (Также ответ можно дать в виде количества акций: нужно купить 50 тыс. акций компании A и 100 тыс. акций компании B.) Стоимость портфеля через год при этом будет равна
$S= 1,65+0,1\cdot 0,5=1,7$ млн руб. независимо от погоды.
Примечание. Как мы видим, оптимальной в данном случае является покупка акций обеих компаний. Это явление получило название диверсификация портфеля или хеджирование рисков. Действительно, если доходность двух акций находится «в противофазe» (экономисты говорят в этом случае об «отрицательной корреляции»), покупка акций второго типа является страховкой от убытков по акциям первого типа, и наоборот.
в) Если Кузьма не платит Гидрометцентру, то, как мы нашли в пункте б), при использовании острожной стратегии он получает 1,7 млн. Рассматривая возможность заплатить гидрометцентру, при осторожной стратегии он должен исходить из плохого прогноза, поскольку там доходность меньше — он будет согласен заплатить $X$, если даже в худшем случае стоимость его портфеля не уменьшится по сравнению с пунктом (б). Если он заплатит сумму $X$, то при плохом прогнозе вложит в акции компании В $(1,5-X)$ млн руб. Стоимость его активов в конце, таким образом, составит $1,4(1,5-X)$.
Чтобы заплатить Гидрометцентру было выгодно, необходимо, чтобы выполнялось неравенство:
$$1,4(1,5-X)\ge 1,7.$$
Отсюда $X\le 2/7$ млн руб.