1. Хитрые издержки
$$TC(Q) =\begin{cases}\frac{Q^2}{5}+10Q+20,\text{ если $Q\le8$;} \\ \frac{Q^2}{5}+100,\text{ если $Q>8$.}\end{cases}$$ .
- Найдите функцию постоянных издержек фирмы;
- При какой минимальной рыночной цене фирма останется на рынке в краткосрочном периоде?
- Интерпретируйте ответ графически.
- Постоянные издержки, по определению, не зависят от выпуска и равны $TC(0)$.
$FC=TC(0)=20.$ -
Искомая цена равна $\min AVC.$ (Почему?)
Восстановим функцию $AVC(Q).$ Для этого нам как раз пригодится найденное значение постоянных издержек.
$$VC(Q)=TC(Q)-FC =\begin{cases}\frac{Q^2}{5}+10Q,\text{ если $Q\le8$;} \\ \frac{Q^2}{5}+80,\text{ если $Q>8$.}\end{cases}$$Значит, $$AVC(Q) =\begin{cases}\frac{Q}{5}+10,\text{ если $Q\le8$;} \\ \frac{Q}{5}+\frac{80}{Q},\text{ если $Q>8$.}\end{cases}$$
При $Q\le 8$данная функция линейна, монотонно возрастает и стремится к 10 при стремлении выпуска к нулю.
При $Q\ge 8$исследуем нашу функцию с помощью производной:
$AVC^{'}(Q)=\frac{1}{5}-\frac{80}{Q^2}=0\Rightarrow Q=20$ - критическая точка нашей функции. Производная меняет знак с минуса на плюс, значит, эта точка является точкой локального минимума.
$AVC(20)=8,$ что меньше 10. Значит, $Q=20$ является также и точкой глобального минимума данной функции; $\min AVC=8,$ что и соответствует искомому значению цены. -
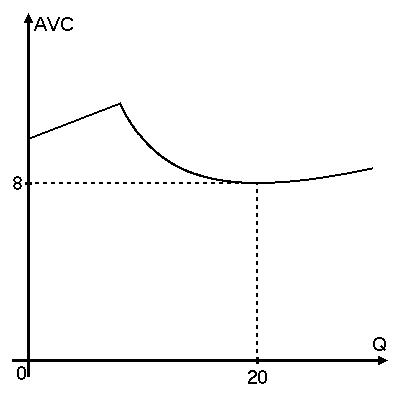
1-й способ иллюстрации. График функции $AVC(Q)$будет иметь вид
2-й способ иллюстрации. График предельных издержек $MC(Q)$будет иметь вид (выделен красным):
2. Марина-монополист
а) Сколько зонтов в день и по какой цене ей нужно продать, если она стремится к максимальной прибыли?
б) Рассчитайте, какую прибыль получает Марина в день.
б) (2 балла) Найдем цену и количество, используя, значение эластичности в точке максимума прибыли.
1-й способ:
$E_{P}^{D}=Q^{'}_{P}\frac{P}{Q}$
$-2=-0.01\frac{P}{12-0.01P}$, отсюда $P=800$.
Подставляем цену в функцию спроса и находим: $Q=12-0.01\times 800=4$.
2-й способ: Нахождение цены и количества исходя из геометрического смысла эластичности.
$\frac{12-Q}{Q}=2$ следовательно, $Q=4$
$\frac{P}{1200-P}=2$ следовательно, $P=800$
2. а) (2 балла) Пусть цена зонта $Х$ рублей (или любое неизвестное число), тогда переменные затраты в день $VC=X\times Q$, постоянные затраты (по условию задачи) равны 200 $(FC=200)$. $TC=VC+FC=X\times Q+200$. Тогда предельные затраты $MC=TC^{'}(Q)=X$ , или любой константе.
б) (2 балла) Чтобы найти функцию общих издержек, нужно найти функцию $МС$.
1-й способ:
Найдем функцию предельной выручки, которая имеет угол наклона в 2 раза больше, чем обратная функция спроса из пункта 1а), то есть $MR=1200-200Q$.
В точке максимума прибыли, при $Q=4$ и $P=800$, выполняется равенство MR и MC.
$$MC+MR=1200-200\times 4=400=X$$
2-й способ:
Запишем индекс Лернера $\frac{P-MC}{P}=\frac{1}{|E_{P}^{D}|}$. Получаем $\frac{800-MC}{800}=1/2$, $МС=400$.
Тогда функция общих издержек имеет вид $TC=400Q+200$
в) (2 балла) Найдем прибыль в точке максимума прибыли: $$\pi =TR-TC=P\times Q-TC=4\times 800-(400\times 4+200)=1200$$
3. Автономные налоги и функция потребления
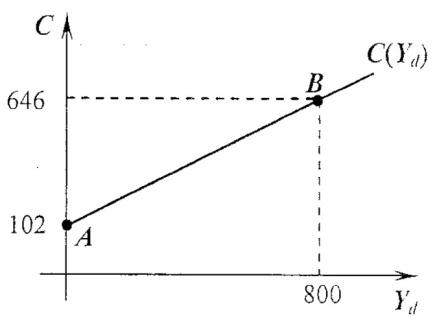
Правительство проводит сдерживающую бюджетно-налоговую политику, увеличивая автономные налоги. На какую величину выросли автономные налоги, если потребление сократилось на $425$?
Чтобы рассчитать значение мультипликатора автономных налогов и определить, как изменился располагаемый доход, найдем значение $MPC$, воспользовавшись информацией о координатах точек A и B функции потребительских расходов:
$$MPC=\frac{646-102}{800-0}=0.68$$
(2 балла)
Тогда из определения $MPC$ получим выражение для $\Delta Y_d$ и определим мультипликатор автономных налогов (можно не определять его отдельно и перейти сразу к следующему шагу, рассчитав значение мультипликатора в ходе определения значения $\Delta T$): $$MPC=\frac{\Delta C}{\Delta Y_d} \rightarrow \Delta Y_d =\frac{\Delta C}{MPC}=-425/0.68=-625 \rightarrow \frac{-MPC}{1-MPC}=-2.125$$
(2 балла)
Теперь можно найти $\Delta T$:
$$\Delta Y_d=\Delta Y-\Delta T=\frac{-MPC}{1-MPC}\times \Delta T-\Delta T \rightarrow -625=-2.125\times \Delta T-\Delta T \rightarrow \Delta T=200$$(2 балла)
4. Европия и Американия
После снятия запрета на свободное перемещение туристов между странами, на мировом рынке туристических услуг установилось равновесие. Описанная ситуация изображена на рисунке (объем измеряется в тыс. туристов).
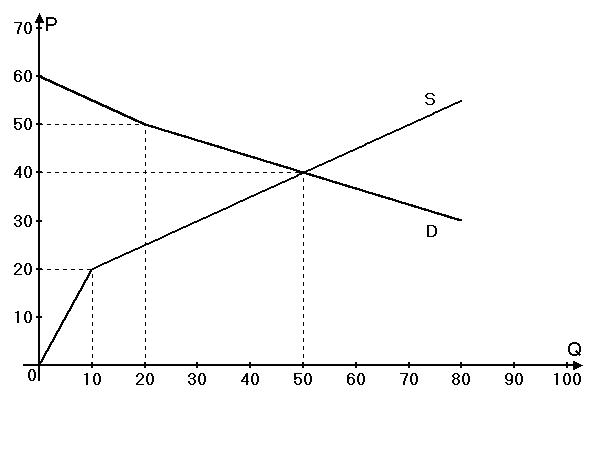
В равновесии поток туристов устремился из Европии в Американию, а не наоборот. При этом количество туристов из Европии, посетивших Американию, превысило 19 тыс. человек. Определите:
- количество туристов из Европии, посетивших Американию;
- количество туристов из Европии, отдохнувших в своей стране;
- количество туристов из Американии, отдохнувших в своей стране.
На более высоком участке мирового спроса спрос предъявляет только одна страна (мы пока не знаем, какая именно).
Продолжим на рисунке этот участок спроса до линии равновесной цены:
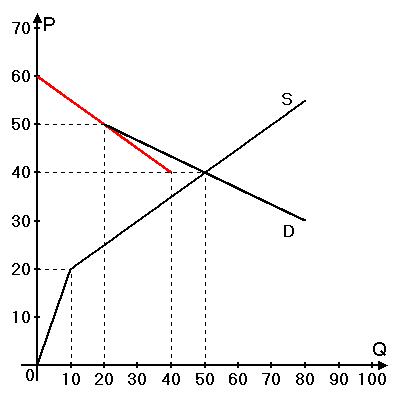
Как видно из рисунка (и любых удобных геометрических соображений, например, равенства треугольников), продолженная прямая пересечет линию равновесной цены в точке $Q=40$. Значит, в равновесии величины спроса двух стран равны 40 и $50 - 40 = 10$.
Поскольку величина спроса Европии никак не меньше 19 (ведь как минимум 19 тыс. чел. из нее отдыхают только за границей, а еще есть те, кто отдыхает дома), то можно заключить, что 40 – это величина спроса Европии, а 10 – величина спроса Американии.
Проделаем такой же «финт» с предложением. Аналогично, на более низком участке мирового предложения туристические услуги готова предлагать только одна страна (и мы опять не знаем, какая именно). Продолжим на рисунке этот участок предложения:
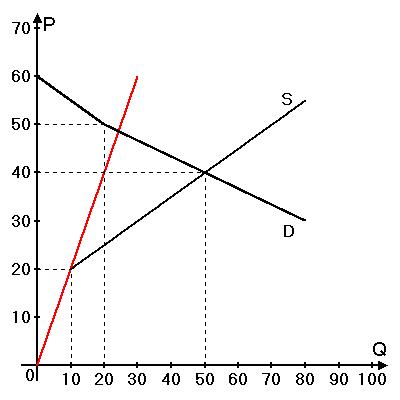
Легко увидеть, что продолженная прямая обязана пересечь линию равновесной цены при $Q=20$ (это, например, следует из того, что наклон этого участка предложения равен 2). Значит, в равновесии величины предложения двух стран равны 20 и $50 - 20 = 30$.
Рассмотрим теперь два случая:
- Величина предложения в Европии равна 30, а в Американии – 20.
В этом случае из Европии едут $40-30=10$ тыс. человек, что невозможно по условию (известно, что количество туристов, выехавших из Европии, превышает 19 тыс.). - Величина предложения в Европии равна 20, а в Американии – 30.
В этом случае из Европии едут отдыхать за границу $40-20=20$ тыс. туристов, что согласуется с условием.
Итак, ответ на первый вопрос – 20 тыс. чел.
Теперь нетрудно ответить на оставшиеся вопросы. Количество туристов из Европии, отдохнувших в своей стране, совпадает с величиной внутреннего предложения в Европии и равно 20 тыс, а количество американийцев, отдохнувших в своей стране, совпадает с величиной внутреннего спроса в Американии и равно 10 тыс.
5. Мировая КПВ или абсолютно мобильная рабочая сила
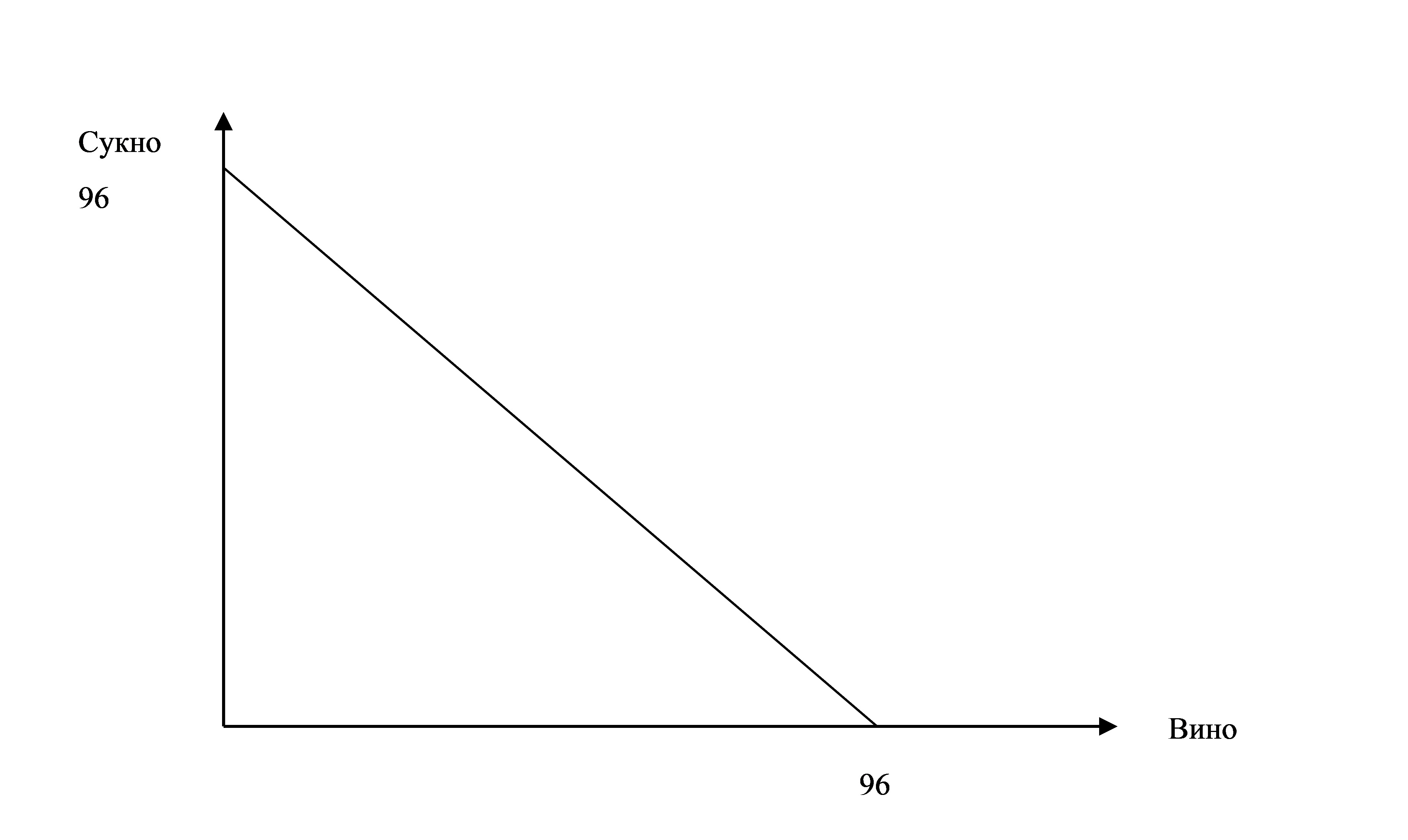
а) Постройте кривые производственных возможностей для Англии, Португалии и для мировой экономики в целом в условиях отсутствия международной торговли. В производстве какого товара каждая из двух стран имеет сравнительное преимущество?
б) Рассчитайте объемы производства и потребления для закрытой экономики каждой страны и мировой экономики в целом. Покажите эти точки на графиках кривых производственных возможностей.
в) Рассчитайте объемы производства и потребления в каждой из стран и в мировой экономике в целом в условиях, когда экономики обеих стран становятся открытыми. Покажите соответствующие точки на кривых производственных и торговых возможностей открытых экономик двух стран и мировой экономики в целом. Рассчитайте объемы экспорта и импорта вина и сукна в каждой из стран.
г) Представим гипотетически, что рабочая сила в мировой экономике абсолютно мобильна. Какой в этом случае будет кривая производственных возможностей для мировой экономики в целом?
Кривая производственных возможностей Англии (1 балл)
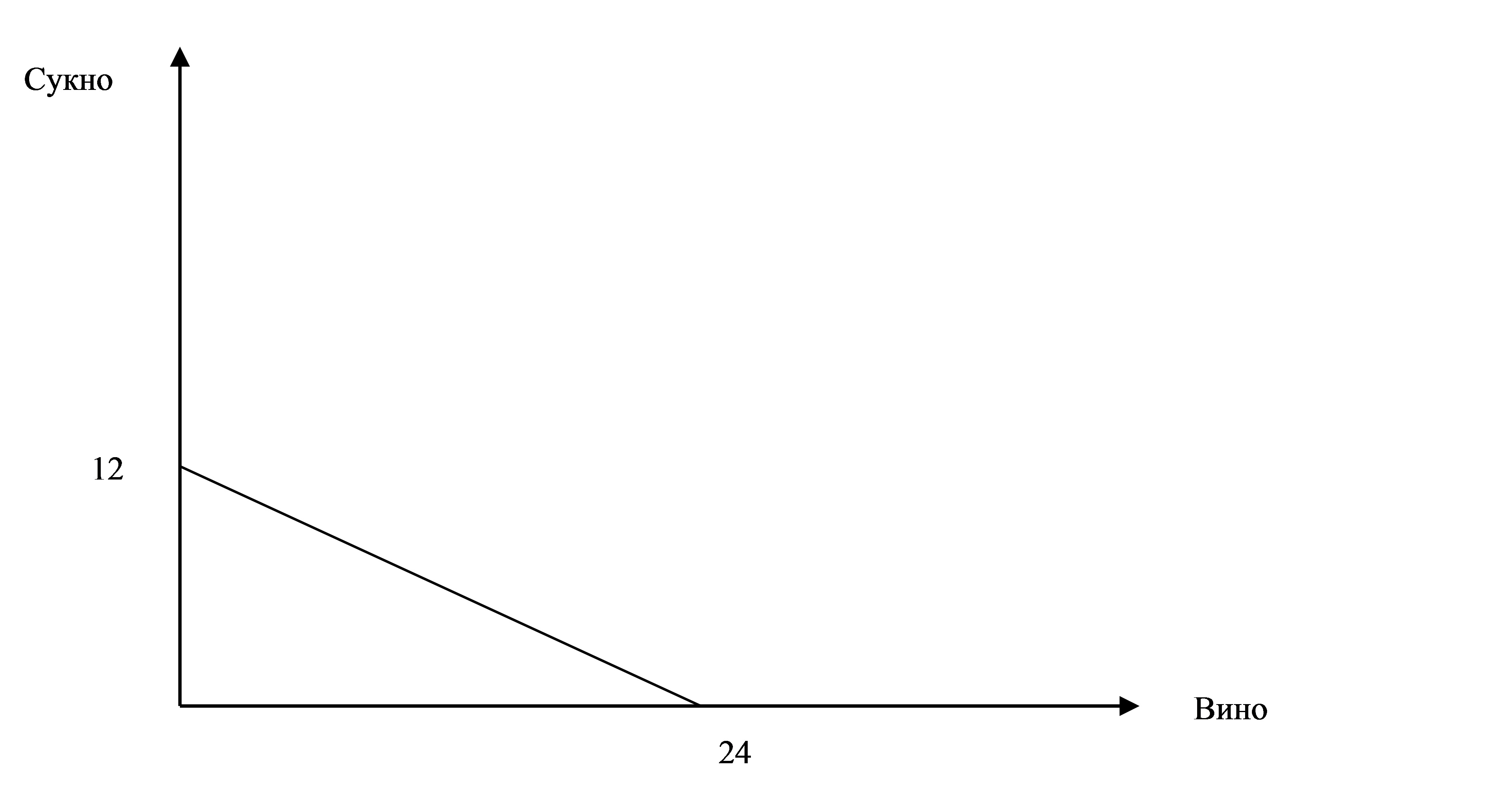
Кривая производственных возможностей Португалии (1 балл)

Кривая производственных возможностей мира строится путем суммирования производственных возможностей двух стран и имеет точку перелома в точке специализации стран, определяемой на основе сравнительного преимущества. Рассчитаем относительные издержки производства (1 балл). В Англии при производстве 1 единицы сукна мы отказываемся от производства 2-х единиц вина, а в Португалии – от одной единицы вина. Относительные издержки производства вина в Англии равны ½, а в Португалии - 1. Таким образом, Англия имеет относительные (сравнительные) преимущества в производстве вина, а Португалия – сукна.
Кривая производственных возможностей мира (1 балл)
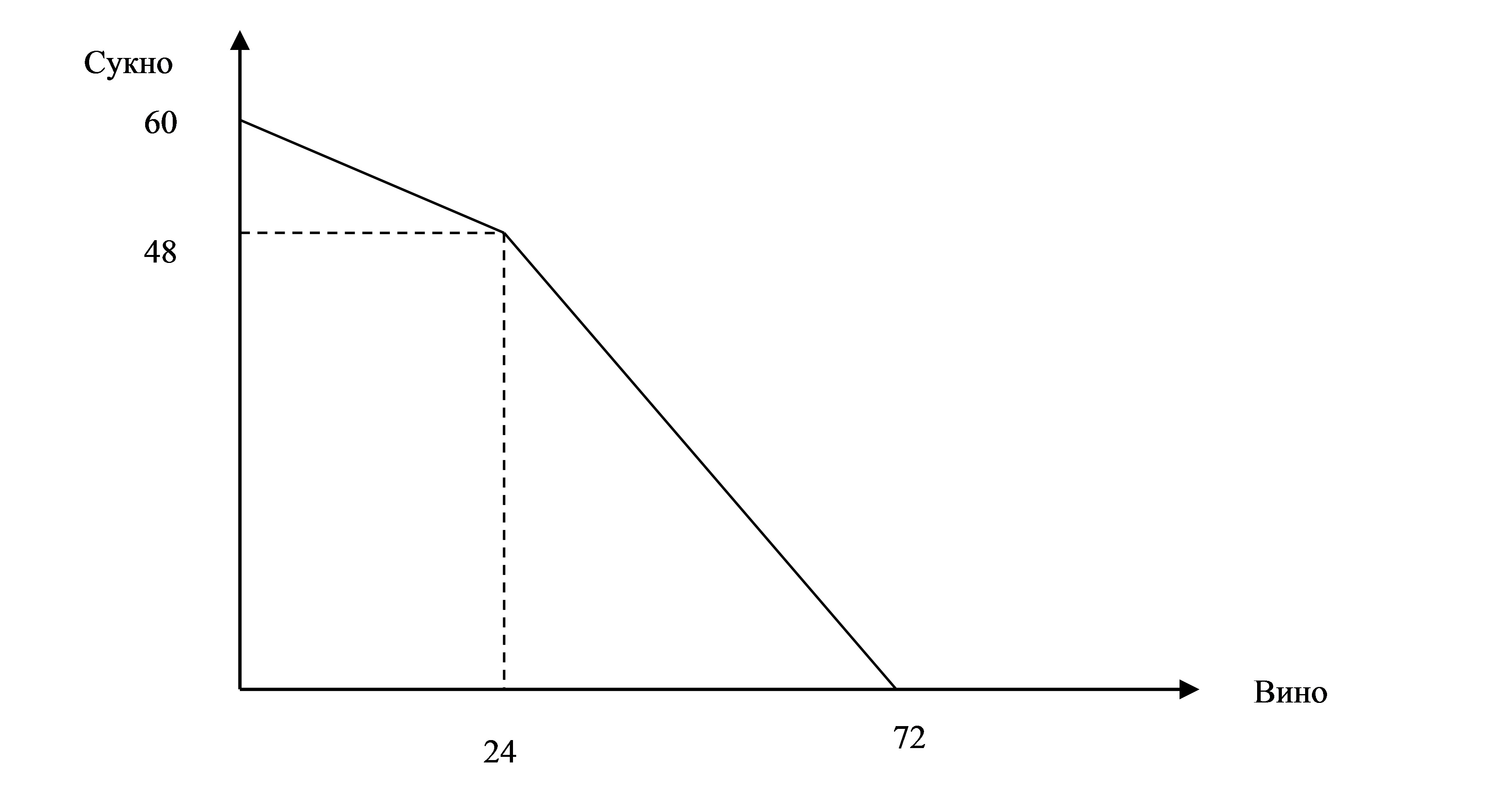
б) (2 балла) В случае закрытой экономики объемы потребления и производства в странах совпадают. Рассчитаем объемы производства и потребления в Англии на основе решения системы уравнений:
$$\begin{cases}
C=B, \ так \ как \ объемы \ потребления \ благ \ одинаковые \ по \ условию \ задачи\\
C=12-0.5B, \ уравнение \ кривой \ производственных \ возможностей
\end{cases}$$
Объемы потребления и производства вина и сукна в Англии в условиях закрытой экономики равны 8.
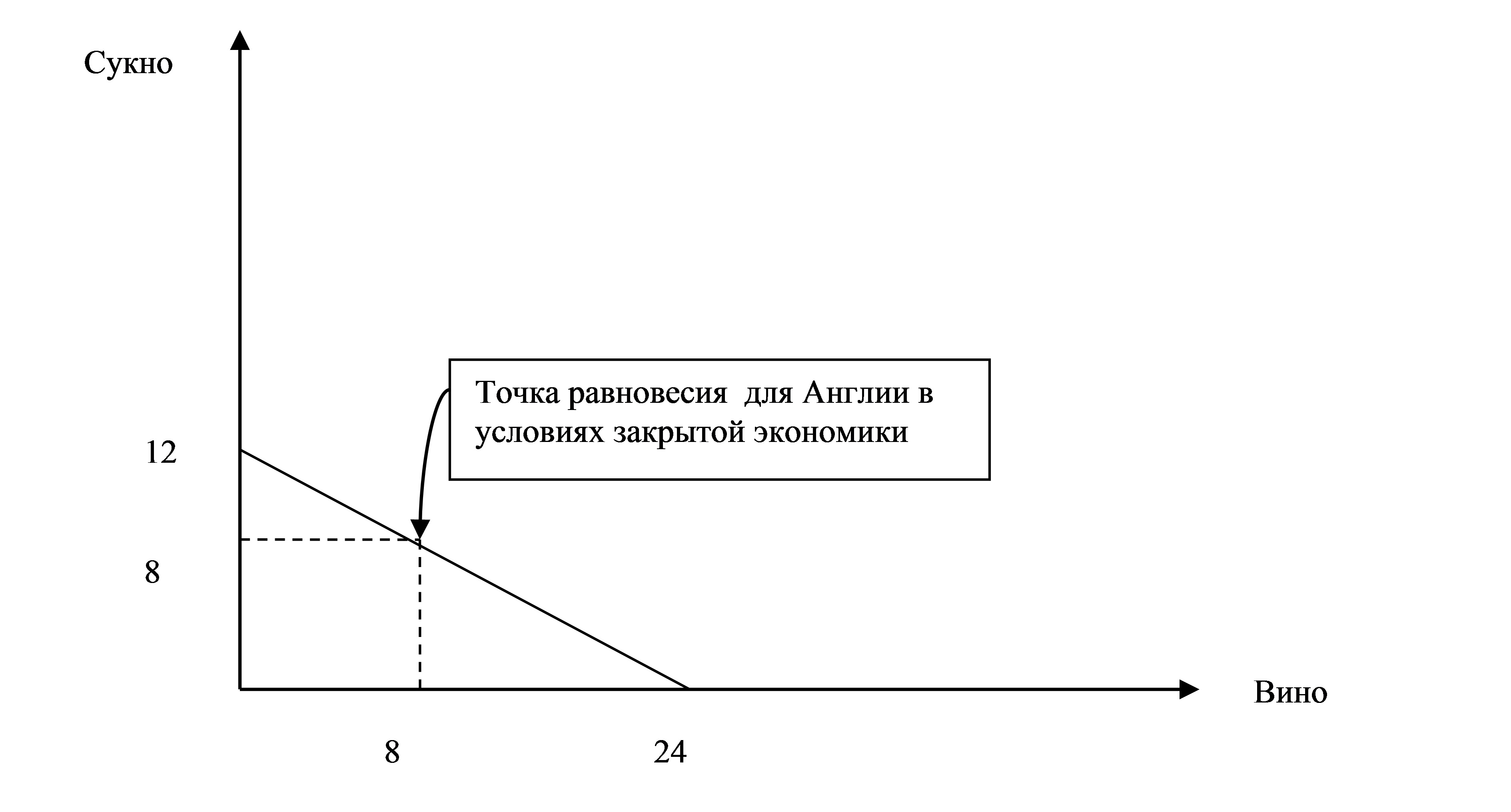
(2 балла) Рассчитаем объемы производства и потребления в Португалии на основе решения системы уравнений:
$$\begin{cases}
C=B, \ так \ как \ объемы \ потребления \ благ \ одинаковые \ по \ условию \ задачи\\
C=48-B, \ уравнение \ кривой \ производственных \ возможностей
\end{cases}$$
Объемы потребления и производства вина и сукна в Португалии в условиях закрытой экономики равны 24.
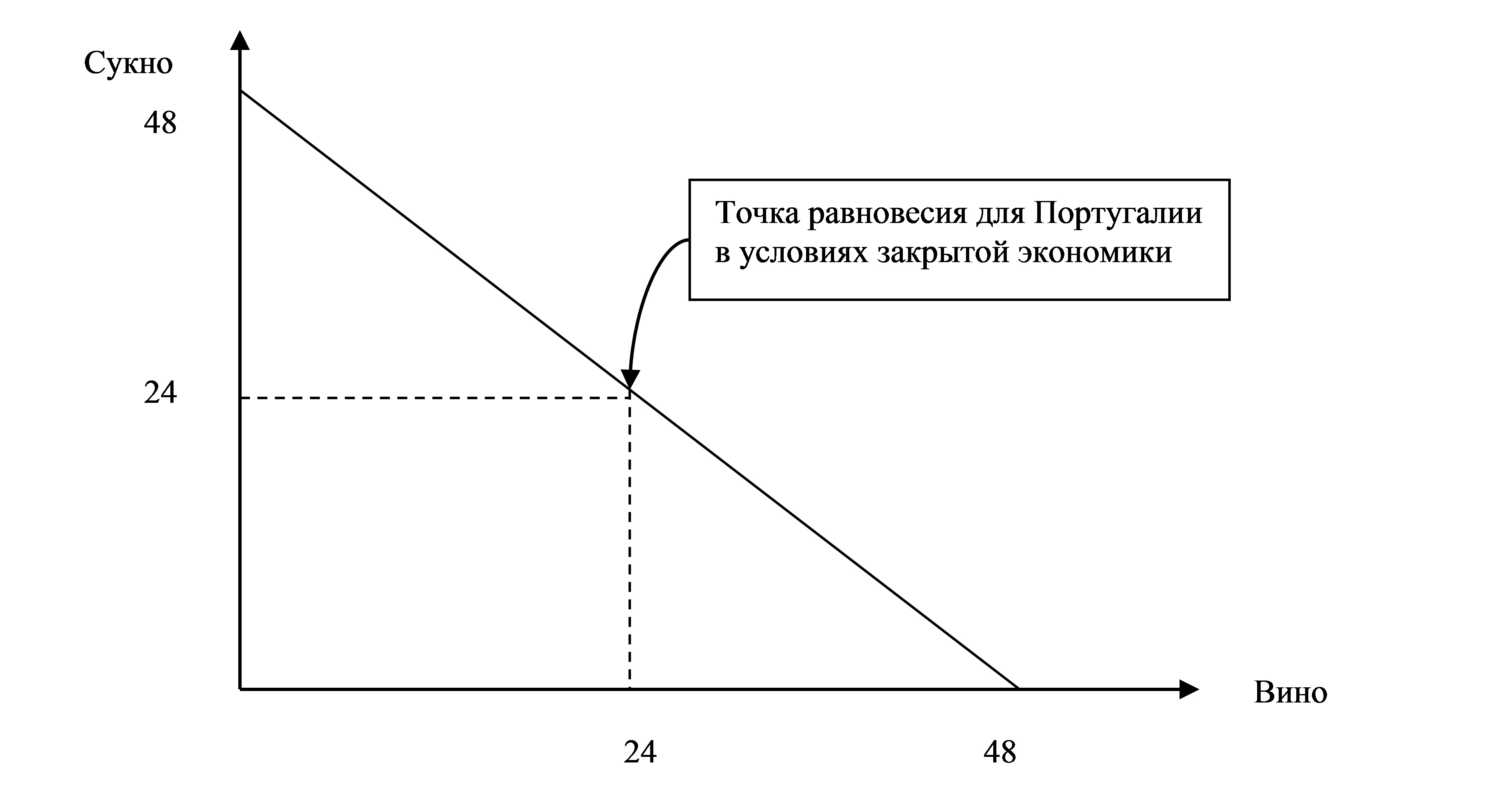
(1 балл) Объемы производства и потребления в мировой экономике равны суммарному производству и потреблению двух стран, то есть сукна и вина производится и потребляется по 32 единицы. Точка равновесия мировой экономики в условиях, когда экономики стран являются закрытыми, лежит ниже кривой производственных возможностей, так как в отсутствие международной торговли не используются сравнительные преимущества стран.
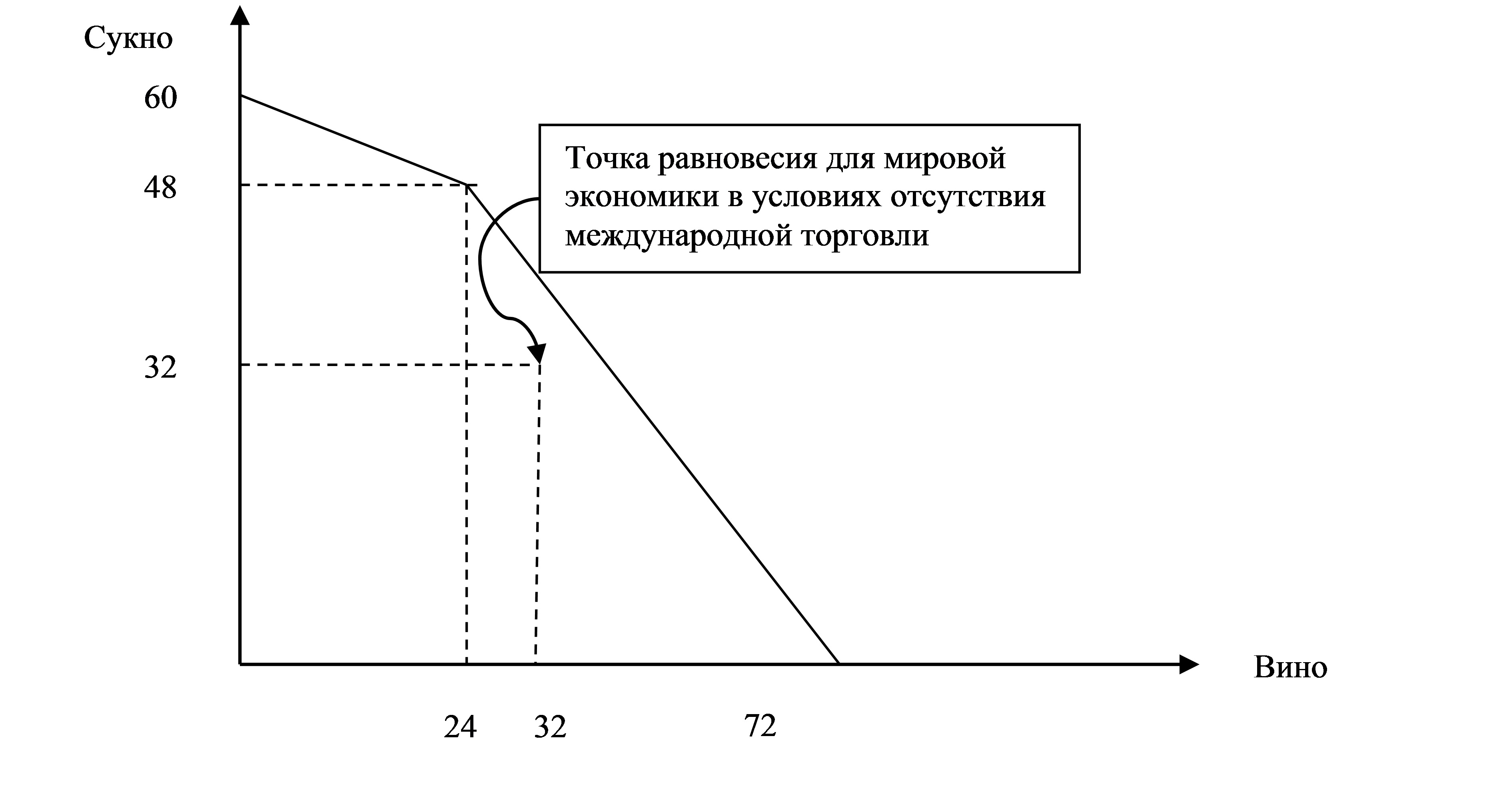
в) (2 балла) В условиях открытой экономики суммарные объемы потребления в двух странах равны суммарным объемам производства и они лежат на кривой производственных возможностей мировой экономики.
$$\begin{cases}
C=B, так \ как \ объемы \ потребления \ благ \ одинаковые \ по \ условию \ задачи\\
C=72-B, \ если \ B<24 \\
C=60-0.5B, \ если \ B\leq 24
\end{cases}$$
Таким образом, объемы производства и потребления в мировой экономике равны: С=36 и В=36, то есть производится и потребляется по 36 единиц сукна и вина. Следовательно, относительные цены равны: С/В=1.
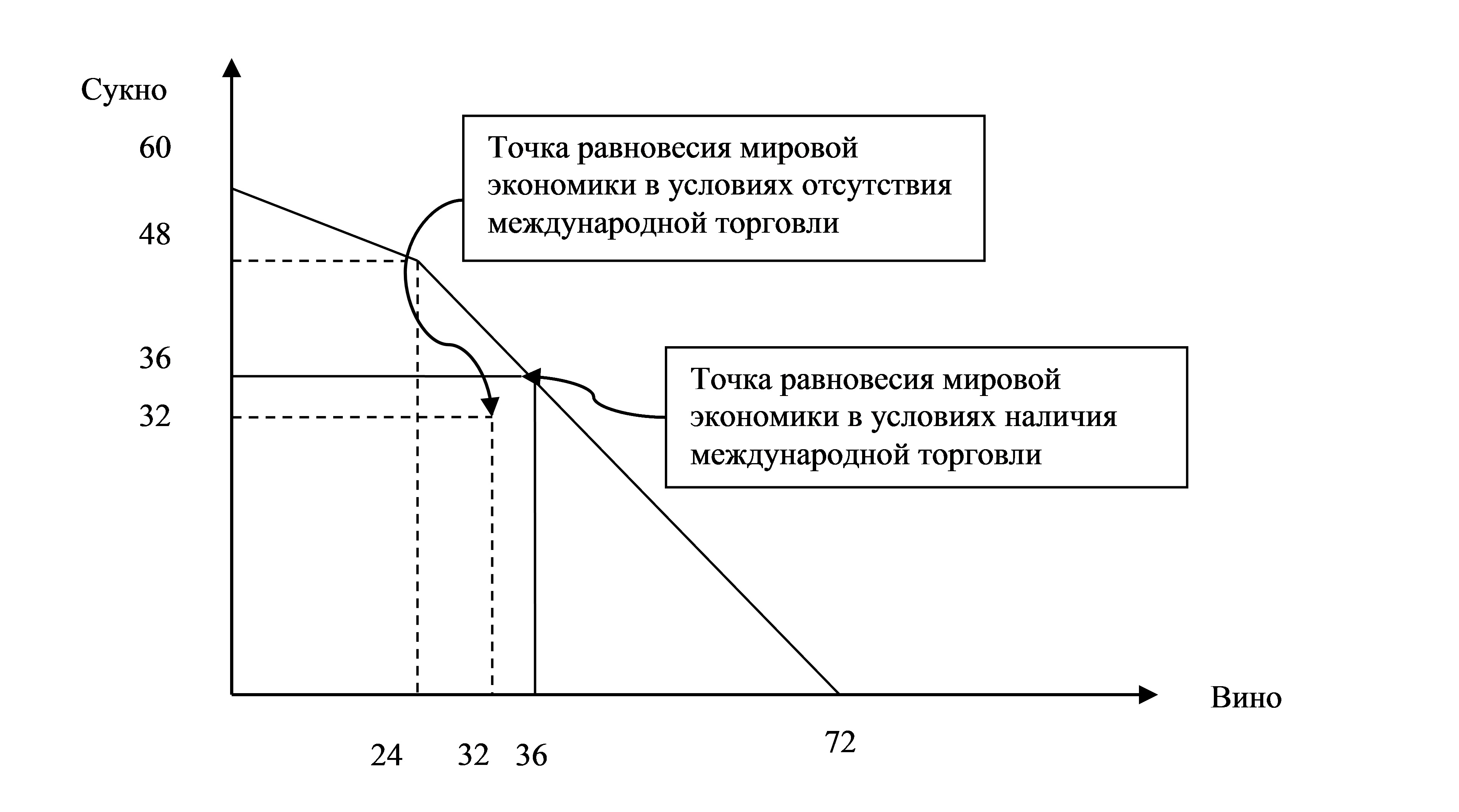
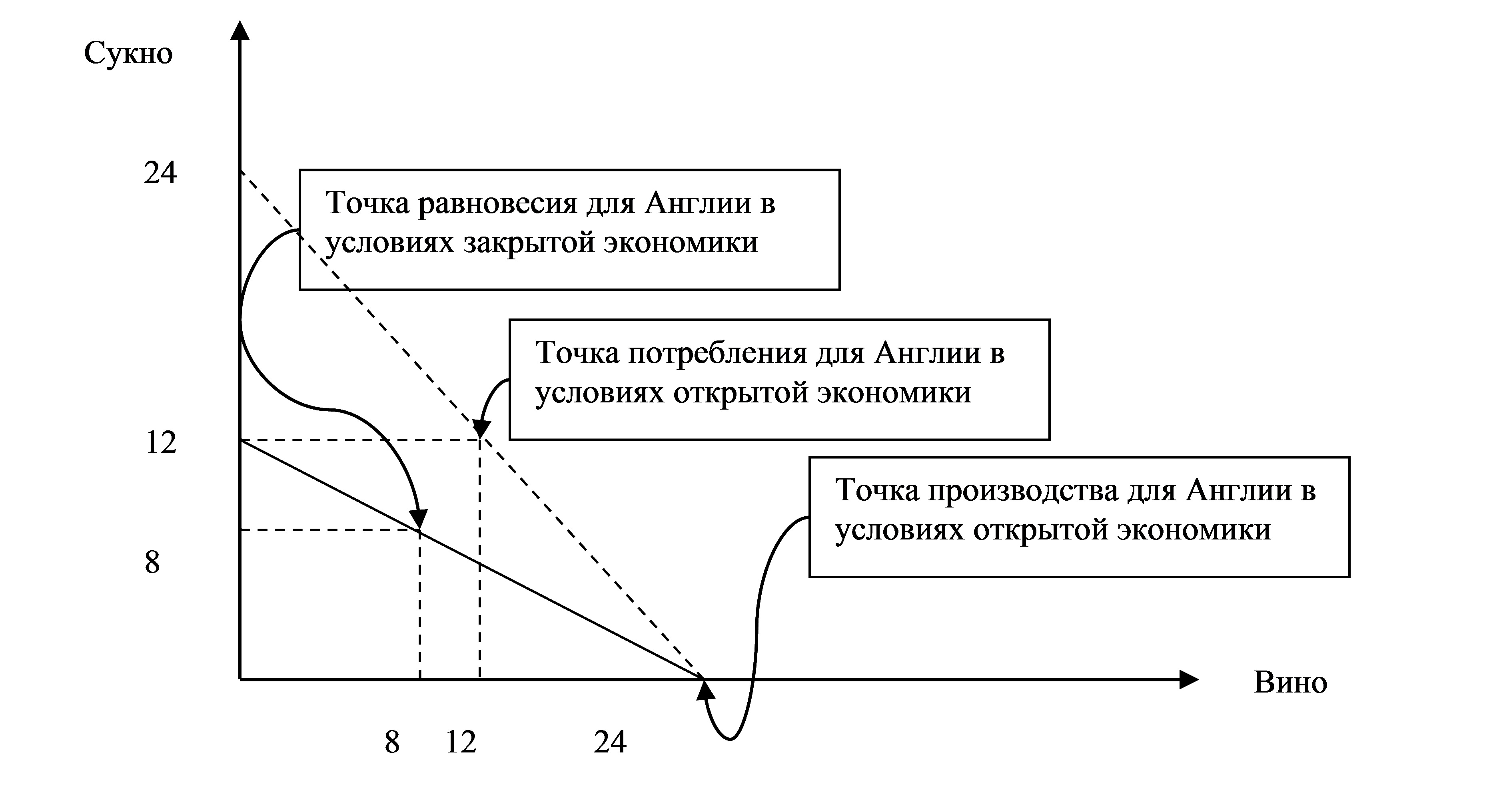
(2 балла) Англия будет производить: 24 единицы вина и не будет производить сукно, то есть В=24, С=0 (полная специализация на товаре, в производстве которого она имеет сравнительное преимущество). Потребление определяется из решения системы уравнений:
$$\begin{cases}
C=B, так \ как \ объемы \ потребления \ благ \ одинаковые \ по \ условию \ задачи\\
C=24-B, \ уравнение \ линии \ мировых \ цен
\end{cases}$$
Потребление в Англии составит: В=С=12, то есть потребляется по 12 единиц вина и сукна. Следовательно, экспорт вина равен 12 и импорт сукна равен 12.
(2 балла) В условиях открытой экономики экспорт должен равняться импорту. Следовательно, в Португалии импорт вина и экспорт сукна равен 12.
Так как цены в Португалии не изменились, то объемы внутреннего потребления благ тоже не изменились : С=В=24, то есть потребляется по 24 единицы сукна и вина.
Объемы производства с учетом объемов экспорта и импорта будут равны: 12 единиц вина (В=12) и 36 единиц сукна (С=36).

г) (2 балла) Так как производительность труда в Португалии выше, как в производстве вина, так и сукна, а мировые цены для обеих стран одинаковы, то уровень заработной платы в Португалии также будет выше: $w=MPL\times P$. В условиях абсолютной мобильности рабочей силы это приведет к миграции всех работников из Англии в Португалию и кривая производственных возможностей для мировой экономики в целом станет прямой линий.