10 класс

1. Труд в Альфа

В стране Альфа производится всего два товара: $x$ и $y$. Для их производства используется единственный ресурс — труд, причём общее количество труда, доступного в Альфе составляет $L=40$.

Выпуск первого товара следующим образом зависит от количества используемого для его производства труда: $x=L_x$.
Выпуск второго товара следующим образом зависит от количества используемого для его производства труда:
$$ y =\begin{cases} 3L_y, & L_y \lt 20 \\
40+L_y, & L_y \geq 20 \end{cases} $$

  1. Постройте КПВ страны Альфа. Укажите на своём рисунке координаты всех ключевых точек.
  2. Жители страны Альфа сами не любят товары, которые они производят. Всю произведённую продукцию они продают на мировом рынке, а на вырученные деньги приобретают импортные товары, которые им нравятся. Известно, что товар $x$ на мировом рынке стоит 2 евро за единицу, а товар $y$ всего 1 евро. Определите максимальную выручку, которую могут получить жители страны Альфа в результате экспорта своих товаров.
  3. Пусть теперь, наоборот, товар y на мировом рынке стоит 2 евро за единицу, а товар $x$ всего 1 евро. Определите максимальную выручку, которую могут получить жители страны Альфа в результате экспорта своих товаров.
Решение

a). Производственная функция для второго товара состоит из двух участков, поэтому при построении КПВ удобно рассмотреть два случая:

Случай 1. $L_y \lt 20$.Этот случай соответствует ситуации: $L_x \gt 20 \Rightarrow x \gt 20$.
$$ \begin{array}{c} L_x+L_y=40 \\ x+\dfrac{1}{3}y=40 \\ y=120-3x \end{array} $$
Случай 2. $L_y \geq 20$. Этот случай соответствует ситуации: $L_x \leq 20 \Rightarrow x \leq 20$.
$$ \begin{array}{c} L_x+L_y=40 \\ x+(y-40)=40 \\ y=80-x \end{array} $$
Таким образом, КПВ задаётся уравнением:
$$ y=\begin{cases} y=80-x, & x \leq 20 \\ 120-3x, & x \gt 20 \end{cases} \qquad (*) $$
Теперь можно построить график:

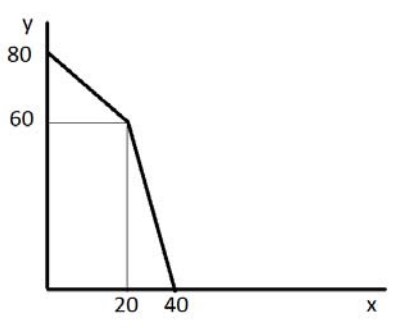
За правильный пункт - 4 балла.

b). В соответствии с КПВ (см. уравнение $(*)$) альтернативные издержки производства каждой из первых 20 единиц товара $x$ равны одной единице товара $y$, то есть 1 евро. В то же время выручка от продажи каждой единицы товара $x$ равна 2 евро. Следовательно, первые 20 единиц товара $x$ производить выгодно.

Далее альтернативные издержки производства каждой дополнительной единицы товара $x$ возрастают до 3 единиц товара $y$, то есть до 3 евро. Следовательно, дальнейшее производство товара $x$ не является выгодным. Таким образом, в этом случае следует производить 20 единиц товара $x$, а все остальные ресурсы направлять на производство товара $y$, что позволит произвести 60 единиц этого товара.

В этом случае выручка составит: $20\cdot2+60\cdot1=100$ евро.

За правильный пункт - 4 балла.

c). В соответствии с КПВ альтернативные издержки одной единицы товара $x$ составляют не менее одной единицы товара $y$, то есть не менее 2 евро. В то же время выручка от продажи одной единицы товара $x$ составляет всего 1 евро. Таким образом, товар $x$ производить невыгодно, и все ресурсы следует направить на производство товара $y$. Это позволит произвести 80 единиц товара $y$, и выручка составит $80\cdot2=160$ евро.

За правильный пункт - 4 балла.

2. 1000 фирм

На совершенно конкурентном рынке действуют 1000 одинаковых фирм, производящих товар $Q$. Функция предельных издержек каждой фирмы $MC(q)=40+200q$, где $q$ – объём продаж одной фирмы. Функция спроса на этот товар имеет вид $Q(P)=280-P$, где $Q$ - совокупный объём продаж, а $P$ – цена товара. Правительство планирует увеличить объём продаж этого товара не менее чем на $10 \%$. Определите минимальный размер адвалорной (% от стоимости товара) субсидии для производителей, которая позволит добиться планируемого увеличения продаж.
Решение

На конкурентном рынке каждая фирма работает, воспринимая цену товара, как заданную, причём каждая фирма будет выпускать такой объём товара, при котором её предельные издержки в точности равны цене товара, т. е. $P=MC(q)=40+200q$. Тогда функция предложения каждой фирмы $q^S(P)=(P-40)/200$. Поскольку таких фирм на рынке 1000, их совокупное предложение $Q^S(P)=1000\cdot \frac{P-40}{200}=5P-200$.

За правильные расчёты - 4 балла

Исходное равновесие на рынке определяется соотношением $Q^D(P)=Q^S(P)$, откуда $5P^*-200=280-P \Rightarrow P^*=80, Q^*=200$.

За правильные расчёты - 2 балла

Если правительство добьется увеличения объема продаж на $10 %$, то будет произведено $200 \cdot (1 + 0{,}1) = 220$ единиц продукции, которую покупатели будут приобретать по цене $280 – 220 = 60$.
Пусть введена адвалорная субсидия для производителей в размере $s$, то если покупатели приобретают товар по цене $P$, производители получают за каждую единицу своей продукции цену $P(1+s)$. Поскольку производители, на конкурентном рынке воспринимают цену товара, как заданную, и производят такой объём товара, при котором цена продукции равна предельным издержкам фирмы, то предложение каждой фирмы можно записать в виде $q^S(P)=\left. \bigl(P(1+s)-40\bigr) \right/ 200$, откуда совокупное предложение всех фирм в отрасли имеет вид:

$Q^S(P)=1000\cdot \dfrac{P(1+s)-40}{200}=5P(1+s)-200$.

Зная, что в новом равновесии фирмам в совокупности необходимо произвести 220 единиц продукции, при цене покупки товара 60, можно найти искомый размер адвалорной субсидии: $220=5\cdot60\cdot (1+s)-200$, откуда $s=0{,}4$.

За правильные расчёты – 4 балла

Увеличение размера адвалорной субсидии будет приводить к тому, что цена покупки товара будет снижаться, а объём продаж возрастать.

3. Параболас и Лаффер

В королевстве Параболас спрос и предложение на мечи задаются линейно. Король захотел ввести потоварный налог с производителей мечей в виде фиксированной суммы за каждый проданный меч. Но Король был мудрым и перед назначением налога решил выяснить как величина налоговых поступлений в бюджет $(T)$ зависит от ставки налога $(t)$.

С помощью исследований, проведённых опытными учёными-экономистами, удалось выяснить, что при ставке налога 2 д.е. и 4 д.е. величина налоговых сборов (то есть величина налоговых поступлений в государственный бюджет) будет одинакова. К тому же выяснилось, что максимальная величина налоговых сборов в результате введения указанного выше налога составит 300 д.е.

Выведите зависимость величины налоговых поступлений в бюджет от ставки налога (кривую Лаффера).

Решение

1). Поскольку спрос и предложение задаются линейно, то кривая Лаффера в королевстве является параболой с ветвями вниз и выглядит следующим образом: $$ T=-\alpha t^2+\beta t $$

За правильную формулу - 3 балла

Замечание: Данный вид кривой можно написать как сразу, исходя из предположений о линейности, так и вывести аналитически. А именно:
$$ \begin{array}{l} Q_d=a-bp \\ Q_s=c+d(p-t) \\ Q_s=Q_d \\ a-bp=c+d(p-t) \\ p^*=\dfrac{a-c}{b+d} +\dfrac{d}{b+d}\cdot t \\ Q^*=a-bp^* \\ Q^*=a-b \left(\dfrac{a-c}{b+d} +\dfrac{d}{b+d}\cdot t \right) \\
Q^*=\left[ a-b \dfrac{a-c}{b+d} \right] - \left[b \dfrac{d}{b+d} \right] t \end{array} $$

Пусть $\left[ a-b \dfrac{a-c}{b+d} \right]=\beta$, а $\left[b \dfrac{d}{b+d} \right]=\alpha$.
К тому же стоит обратить внимание, что $\alpha \gt 0$ (за счёт того, что $b \gt 0$ и $d \gt 0$). Тогда:

$$\begin{array}{c} Q^*=\beta -\alpha t \Rightarrow T=tQ^* \\ T=-\alpha t^2 + \beta t \end{array} $$
2). Известно, что $T(2)=T(4)$. Это означает, что: $$\begin{array}{c} -\alpha \cdot 2^2+\beta \cdot 2 = -\alpha \cdot 4^2+\beta \cdot 4 \\
-4\alpha+2\beta=-16\alpha+4\beta \\
12\alpha=2\beta \\ 6\alpha=\beta \end{array} $$
За правильные расчёты - 2 балла

Таким образом, можем записать, что: $T=-\alpha t^2 + 6\alpha t $.

3). Поскольку это парабола, направленная ветвями вниз, то мы можем определить её вершину: $$ t_{верш}=-\dfrac{6\alpha}{2\cdot (-\alpha)}=3$$
Замечание: $t=3$ можно найти и с помощью того, что $t=2$ и $t=4$ находятся от вершины на равном расстоянии. То есть достаточно посчитать среднее между 2 и 4.

За правильные расчёты - 2 балла

4). Нам известно, что $T_{max}=300$. К тому же: $$T_{max}=T(t_{верш})=-\alpha\cdot3^2+6\alpha\cdot3=-9\alpha+18\alpha=9\alpha$$
Исходя из этого: $9\alpha=300 \Rightarrow \alpha=\dfrac{100}{3}, \beta=200$

5). Теперь мы можем вывести зависимость величины налоговых поступлений в бюджет от ставки налога: $$T=-\dfrac{100}{3}t^2+200t$$
За правильные расчёты - 3 балла

4. Газированный "Южный"

В регионе Северный функция спроса на газированный напиток «Южный» $Q^D(P)=320-2P$, где $Q$ и $P$ выражены в соответствующих условных единицах. Средние переменные издержки единственной компании, которая поставляет напиток «Южный» во все точки его продаж в регионе постоянны и равны 20. Кроме того, компания несёт фиксированные затраты в размере 10. Региональные власти хотели бы сократить объём потребления газированных напитков, получив при этом от компании выплаты в бюджет региона. С этой целью власти вводят налог по ставке $t$ за каждую проданную единицу продукции. Налог вводится таким образом, чтобы максимизировать выплаты в региональный бюджет. На сколько процентов при этом сократится объём потребления газированного напитка и на сколько (в %) изменится его цена?
Решение

Прибыль компании, которая при данных условиях задачи действует как монополист, имеет вид:
$П=\left(160-\dfrac{Q}{2}\right) Q -20Q-10$, где учтено, что обратная функция спроса $P^D(Q)=160-\dfrac{Q}{2}$, а переменные издержки компании $VC=AVC(Q)\cdot Q=20Q$.

За правильные расчёты - 2 балла

Выражение для прибыли представляет собой квадратичную функцию, графиком которой является парабола, ветви которой в пространстве $(Q,П)$ направлены вниз. Тогда, максимизируя прибыль, компания будет производить Q^*=140 по цене P^*=160-\dfrac{140}{2}=90$.

За правильные расчёты – 2 балла

Если региональные власти вводят налог по ставке $t$, то прибыль компании составит: $$\tilde{П}=\left(160-\dfrac{Q}{2}\right) Q -20Q-10-tQ$$
За правильные расчёты – 1 балл

Тогда, максимизируя прибыль, компания будет производить $\tilde{Q}=140-t$. При этом выплаты в региональный бюджет составят $T=t\tilde{Q}=t\cdot (140-t)$. Графически эта функция представляет собой в координатах $(t,T)$ параболу, ветви которой направлены вниз, поэтому максимальный доход от налогообложения власти смогут получить, если налог составит $\tilde{t}=70$. При таком налоге будет продано $\tilde{Q}=140-70=70$ по цене $\tilde{P}=160-\dfrac{70}{2}=125$

За правильные расчёты – 3 балла

Объём продаж напитка после введения налога сокращается вдвое, следовательно, снижается на $50 \%$.
Цена напитка возрастает на $100\cdot \dfrac{125-90}{90} \approx 38 \%$

За правильные расчёты – 2 балла

11 класс

1. Необычная КПВ

Про кривую производственных возможностей страны известно следующее: альтернативная стоимость производства икса $(x)$, выраженная в единицах игрека $(y)$, следующим образом зависит от $(y)$:
$$AC_x=\dfrac{1}{2y} (\text{единиц } y)$$
При этом известно, что точка $(10;0)$ в координатах $(x; у)$ лежит на КПВ.

Жители страны потребляют товар икс и игрек в пропорции $1:\alpha$, где $\alpha$ - целое положительное число. Также известно, что в равновесии потребляется целое количество и икса, и игрека.

Определите, в какой пропорции жители предпочитают потреблять икс и игрек.

Решение

Как известно, альтернативная стоимость производства единицы икса равна тому количеству единиц игрека, от которых нам придётся отказаться (дискретный случай).

В непрерывном же случае, когда мы имеем дело с функцией, удобнее воспользоваться производной. Действительно, производная функции в каждой конкретной точке показывает, как известно, скорость изменения значения функции при «маленьком» изменении аргумента.

Альтернативные издержки производства одной единицы товара $x$ равны: $$AC_x=-\dfrac{1}{x'_y}$$
Минус возникает в связи с тем, что принято говорить об альтернативной стоимости как о положительной величине.
(Рассмотрим пример КПВ с постоянной альтернативной стоимостью. КПВ будет иметь линейный вид, например, $y = 10 – 2x$. Понятно, что равенство в терминах альтернативной стоимости выглядит так: $10 \cdot y = 5 \cdot x$ или $y = 0{,}5 \cdot x$ – чтобы произвести один игрек, нужно отказаться от $0{,}5x$. Этот же результат можно получить, используя производную: $y'_x=-2$. Тогда альтернативная стоимость игрека: $AC_y=-\dfrac{1}{y'_x}=0{,}5$ единиц икса).

1). Зная альтернативную стоимость икса, как функцию от игрек находим КПВ: $$AC_x=-\dfrac{1}{x'_y}=\dfrac{1}{2y} \Rightarrow x'_y=-2y$$
Подбираем функцию, производная которой равна $(-2y)$:
Получаем, что $x=-y^2+C$, где $С$ – некоторая константа.

За правильные расчёты - 4 балла

2). Т.к. точка $(10;0)$ находится на КПВ, находим константу $C$: $$\begin{array}{c} 10=-0+C \\ C=10 \end{array}$$
Итак, уравнение КПВ в этой экономике выглядит так: $x+y^2=10$

За правильные расчёты - 2 балла

3) Жители страны потребляют товар икс и игрек в пропорции $1:\alpha$. Следовательно, в равновесии должно выполняться соотношение: $y=\alpha x$.
Далее нужно, опираясь на целочисленность икса, игрека и альфы, подобрать равновесие.

Самое простое – перебором.

Т. к. $x+y^2=10$ и $y$ – целое, то $0 \lt y \leq 3$ («Жители страны потребляют товар икс и игрек в пропорции $1:\alpha$», поэтому $y \neq 0$).
Остается 3 варианта: $(9;1), (6;2), (1;3)$. Подставляем их в $y=\alpha x$, получаем, что все целое только, если $x = 1; y = 3$.

За правильные расчёты - 4 балла

2. Про эластичность и налоги

На рассматриваемом рынке выполняются законы спроса и предложения. Известно, что произведение эластичностей спроса и предложения по цене постоянно и равно (–1), а их сумма также постоянна и равна 0. Выручка производителей в равновесии равна 200.

Если государство вмешается и установит потоварный налог на производителя в размере 3 ед. за каждую проданную единицу товара, то равновесная цена вырастет в 2 раза.

Определите равновесное количество товара до вмешательства государства.

Решение

«На рассматриваемом рынке выполняются законы спроса и предложения. Известно, что произведение эластичностей спроса и предложения по цене постоянно и равно (–1), а их сумма также постоянна и равна 0».
Отсюда получаем, что одна эластичность постоянна и равна 1, а другая: (–1).

За правильные расчёты - 3 балла

Т. к. законы спроса и предложения выполняются, то: $$Q^D=\dfrac{B}{p}; Q^S=Ap$$.
Выручка производителя равна: $p_0\cdot \dfrac{B}{p_0}=B=200$
Поэтому $B=200, Q^D=\dfrac{200}{p}$

За правильные расчёты - 3 балла

До вмешательства государства: $Ap_0=\dfrac{200}{p_0}$

После вмешательства государства: $A(2p_0-3)=\dfrac{200}{p}$

За правильные расчёты – 3 балла

Решая систему из двух последних уравнений, находим, что $p_0=2$. Следовательно, $Q_0=100$.

За правильные расчёты – 1 балл

3. Труд в Альфа

В стране Альфа производится всего два товара: $x$ и $y$. Для их производства используется единственный ресурс — труд, причём общее количество труда, доступного в Альфе составляет $L=40$.

Выпуск первого товара следующим образом зависит от количества используемого для его производства труда: $x=L_x$.
Выпуск второго товара следующим образом зависит от количества используемого для его производства труда:
$$ y =\begin{cases} 3L_y, & L_y \lt 20 \\
40+L_y, & L_y \geq 20 \end{cases} $$

  1. Постройте КПВ страны Альфа. Укажите на своём рисунке координаты всех ключевых точек.
  2. Жители страны Альфа сами не любят товары, которые они производят. Всю произведённую продукцию они продают на мировом рынке, а на вырученные деньги приобретают импортные товары, которые им нравятся. Известно, что товар $x$ на мировом рынке стоит 2 евро за единицу, а товар $y$ всего 1 евро. Определите максимальную выручку, которую могут получить жители страны Альфа в результате экспорта своих товаров.
  3. Пусть теперь, наоборот, товар y на мировом рынке стоит 2 евро за единицу, а товар $x$ всего 1 евро. Определите максимальную выручку, которую могут получить жители страны Альфа в результате экспорта своих товаров.
Решение

a). Производственная функция для второго товара состоит из двух участков, поэтому при построении КПВ удобно рассмотреть два случая:

Случай 1. $L_y \lt 20$.Этот случай соответствует ситуации: $L_x \gt 20 \Rightarrow x \gt 20$.
$$ \begin{array}{c} L_x+L_y=40 \\ x+\dfrac{1}{3}y=40 \\ y=120-3x \end{array} $$
Случай 2. $L_y \geq 20$. Этот случай соответствует ситуации: $L_x \leq 20 \Rightarrow x \leq 20$.
$$ \begin{array}{c} L_x+L_y=40 \\ x+(y-40)=40 \\ y=80-x \end{array} $$
Таким образом, КПВ задаётся уравнением:
$$ y=\begin{cases} y=80-x, & x \leq 20 \\ 120-3x, & x \gt 20 \end{cases} \qquad (*) $$
Теперь можно построить график:

За правильный пункт - 4 балла.

b). В соответствии с КПВ (см. уравнение $(*)$) альтернативные издержки производства каждой из первых 20 единиц товара $x$ равны одной единице товара $y$, то есть 1 евро. В то же время выручка от продажи каждой единицы товара $x$ равна 2 евро. Следовательно, первые 20 единиц товара $x$ производить выгодно.

Далее альтернативные издержки производства каждой дополнительной единицы товара $x$ возрастают до 3 единиц товара $y$, то есть до 3 евро. Следовательно, дальнейшее производство товара $x$ не является выгодным. Таким образом, в этом случае следует производить 20 единиц товара $x$, а все остальные ресурсы направлять на производство товара $y$, что позволит произвести 60 единиц этого товара.

В этом случае выручка составит: $20\cdot2+60\cdot1=100$ евро.

За правильный пункт - 4 балла.

c). В соответствии с КПВ альтернативные издержки одной единицы товара $x$ составляют не менее одной единицы товара $y$, то есть не менее 2 евро. В то же время выручка от продажи одной единицы товара $x$ составляет всего 1 евро. Таким образом, товар $x$ производить невыгодно, и все ресурсы следует направить на производство товара $y$. Это позволит произвести 80 единиц товара $y$, и выручка составит $80\cdot2=160$ евро.

За правильный пункт - 4 балла.

4. Монопсония на рынке труда

Фирма «Альфа» функционирует в регионе М и производит товар Игрек. При этом «Альфа» является единственным агентом на рынке труда, который предъявляет спрос на трудовые ресурсы, производящие товар Игрек. Предельный доход продукта труда компании имеет вид $MRP^A_L(L)=120-\dfrac{L}{7}$. Предложение трудовых ресурсов в регионе М, которые могут быть заняты в производстве товара Игрек: $L^S(w)=6w-120$, где $w$ – заработная плата в тыс. руб.

Каковы заработная плата, численность занятых и уровень безработицы в регионе?

Решение

Компания «Альфа» является монопсонистом на рынке труда. Равновесие на рынке определяется условием: предельный доход продукта труда компании должен быть равен предельным расходам на единицу труда (работника). Так как заработная плата не воспринимается компанией как заданная, а зависит от количества нанятых работников, то $$MRP^A_L(L)=\bigl(w(L)\cdot L \bigr)'=\bigl( (20+L/6) \cdot L \bigr)'$$

За правильные расчёты - 6 баллов

Из этого следует, что: $120-\dfrac{\tilde{L}}{7}=20+\dfrac{\tilde{L}}{3}$, и $\tilde{L}=210$ тыс. человек.
Так как предельный доход продукта труда является убывающей линейной функцией, а предложение труда – возрастающей линейной функцией, то $\tilde{L}$ гарантирует компании получение в данных условиях максимальной прибыли. Заработная плата при этом составит $20 + 210/6 = 55$ тыс. руб.

За правильные расчёты - 3 балла

При данной заработной плате все работники, желающие работать, будут наняты, поэтому безработица в регионе отсутствует (1 балл).

7-8 класс

1. Манипуляции с вкладом

Федя захотел вложить деньги в иностранный банк. Для этого он обменял имеющиеся у него 87 500 рублей на доллары по курсу 35 рублей за 1 доллар. После этого Федя вложил всю сумму в иностранный банк на три года под 10 % годовых (это означает¸ что сумма вклада в банке ежегодно увеличивалась на 10 % по отношению к оставшейся на конец года). Через три года Федя забрал всю имеющуюся на счёте сумму и перевёл её обратно в рубли по курсу 40 рублей за 1 доллар. Какую прибыль (в рублях) получил Федя?
Решение

1-й способ (рациональный):

  1. Разделим сначала $87 500$ на $35$. Получим $2500$ долларов. (2 балла)
  2. Умножим $2500$ на $40$. Получим $100 000$ рублей (сколько бы Федя получил просто за счёт ослабления рубля). (2 балла)
  3. Посчитаем $1,1$ в третьей степени. Получаем $1{,}331$. (2 балла)
  4. Умножим $1{,}331$ на $100 000$. Получаем $133 100$. (2 балла)
  5. Осталось только вычесть полученную сумму из первоначальной: $133100-87 500=45 600.$ (2 балла)

2-й способ (нерациональный):

  1. Разделим $87 500$ на $35$. Получаем $2500$ долларов. (2 балла)
  2. Посчитаем $1,1$ в третьей степени. Получаем $1,331$. (2 балла)
  3. Умножим $2500$ на $1,331$. Получаем $3327,5$ долларов. (2 балла)
  4. Умножим $3327,5$ на $40$. Получаем $133 100$ рублей. (2 балла)
  5. Вычитаем из полученной суммы первоначальную; $133100-87 500$. Получаем $45 600$. (2 балла)

2. Ранок паровозов

Фирма «Гудок» является единственным производителем на рынке паровозов в некоторой стране. У фирмы есть шесть потенциальных покупателей, каждый из которых раздумывает над покупкой одного паровоза. Максимальная цена, которую первый покупатель согласен заплатить за паровоз, составляет 1000 монет. Второй покупатель согласен заплатить за паровоз не более 800 монет. Третий – не более 600. Четвёртый – не более 400. Наконец, пятый и шестой покупатели согласны заплатить за паровоз максимум по 200 монет. По местным законам фирма обязана продавать все паровозы по одинаковой цене. Какую цену ей следует установить для получения наибольшей выручки?
Решение

Составим наглядную таблицу:

Цена Количество покупателей по данной цене $\begin{array}{c} \text{Выручка}= \\ \text{Цена} \cdot \text{Количество} \\ \textbf{За формулу - 2 балла}\end{array}$
1000 1 1000
800 2 1600
600 3 1800 максимальное значение
400 4 1600
200 6 1200

3. Забор вокруг школы

Городские власти выделили 1,2 млн руб. на строительство забора вокруг территории школы. Территория вокруг школы имеет прямоугольную форму площадью 0,9 га, которую с севера и юга необходимо оградить деревянным забором, а с востока и запада – металлическим. Установка одного метра деревянного забора обходится в 5 тыс. рублей, металлического – в 2 тыс. рублей. Найдите все возможные значения каждой стороны ограждаемой территории, при которых выделенной на строительство суммы будет достаточно.
Решение

Пусть $X$ – длина одной стороны, а $Y$ – ширина другой стороны. В прямоугольнике противоположные стороны равны.

Площадь территории:
$X\cdot Y = 9000m^2 \Rightarrow Y=\dfrac{9000}{X}$ За формулу - 2 балла.

Расходы на строительство:
$\begin{array}{l} 5\cdot2X+2\cdot2 \dfrac{9000}{X} \leq 1200 \textbf{ За формулу - 4 балла} \\
10X+\dfrac{36000}{X}\leq 1200 \\
X+\dfrac{3600}{X}\leq 120 \\
X^2+3600\leq 120X \\
\text{Дискриминант равен нулю, поэтому один корень}\\
X=-\dfrac{b}{2a}=60 \\ Y=\dfrac{9000}{60}=150 \textbf{ За число - 4 балла}\end{array}$

Таким образом, выделенной суммы будет достаточно только в том случае, если длина одной стороны будет не больше 60 м, а ширина другой – не больше 150 м.

4. Яблочная

Функция предложения яблок имеет вид $Q_s=100p-300$, где $Q_s$ – величина рыночного предложения яблок в килограммах, а $p$ – цена одного килограмма яблок в денежных единицах (д.е.). Яблоки приобретают множество потребителей, каждый из которых имеет индивидуальную функцию спроса $q_d=12-p$, где $q_d$ – величина индивидуального спроса каждого потребителя на яблоки в килограммах. Известно, что в равновесии суммарная выручка производителей яблок составила $1800$ д.е. Определите число потребителей на рынке.

Решение

Зная равновесную выручку, можно найти равновесную цену товара:

$\begin{array}{l} pQ=1800 \quad \textbf{ За формулу - 2 балла} \\ p(100p-300)-1800\end{array}$

Это квадратное уравнение имеет два корня: $-3$ и $6$. Цена может быть только положительной, следовательно, $p=6$. За число – 4 балла. Подставив эту цену в функцию предложения, находим равновесное количество товара $Q=100\cdot6-300=300$.

Величина спроса одного потребителя по такой цене составляет $q_d=12-6=6$.

Таким образом, каждый из потребителей покупает шесть единиц товара, а всего на рынке приобретается $300$ единиц товара. Следовательно, общее число потребителей на рынке составляет:

$\dfrac{300}{6}=50 \quad \textbf{ За число - 4 балла}$

9 класс

1. Ранок паровозов

Фирма «Гудок» является единственным производителем на рынке паровозов в некоторой стране. У фирмы есть шесть потенциальных покупателей, каждый из которых раздумывает над покупкой одного паровоза. Максимальная цена, которую первый покупатель согласен заплатить за паровоз, составляет 1000 монет. Второй покупатель согласен заплатить за паровоз не более 800 монет. Третий – не более 600. Четвёртый – не более 400. Наконец, пятый и шестой покупатели согласны заплатить за паровоз максимум по 200 монет. По местным законам фирма обязана продавать все паровозы по одинаковой цене. Какую цену ей следует установить для получения наибольшей выручки?
Решение

Составим наглядную таблицу:

Цена Количество покупателей по данной цене $\begin{array}{c} \text{Выручка}= \\ \text{Цена} \cdot \text{Количество} \\ \textbf{За формулу - 2 балла}\end{array}$
1000 1 1000
800 2 1600
600 3 1800 максимальное значение
400 4 1600
200 6 1200

2. Обувь со скидкой

Хозяин небольшого обувного магазина решил избавиться от части запасов обувной продукции на складе и увеличить объём продаж. Для этого он объявил акцию: «Все товары продаются в рассрочку. При одновременной покупке двух пар обуви заплати сейчас полную стоимость первой пары и $60 \%$ от стоимости второй. Остальная сумма выплачивается по $Z \%$ от стоимости пары $P$ каждый следующий месяц». Студент Экономов решил обновить свою обувь и купил по этой акции две пары ботинок на деньги, которые он заработал летом.

  1. Какую ставку процента $Z \%$ от стоимости $P$ будет выплачивать студент ежемесячно, если известно, что к концу зимней сессии (через 5 месяцев) он оплатит только $80 \%$ стоимости $P$?
  2. Через сколько месяцев студент вернёт оставшуюся сумму полностью, считая от дня покупки ботинок?
Решение

1). Через 5 лет он заплатит $0{,}8P$ или $0{,}6P+5\cdot \dfrac{Z}{100} \cdot P =0{,}8\cdot P$
Отсюда получаем:
$ 20=5Z $
$ Z=4 \% $

Ответ: ежемесячно студент будет платить $4 \%$ от стоимости $P$.
За правильные расчёты – 5 баллов.

2). Студенту осталось заплатить $40 \%$ от $P$.
Величина оставшейся суммы, которую студент должен вернуть продавцу равна $\left( \dfrac{Z}{100} \cdot \text{количество месяцев} \right) \cdot P$ или $0{,}4P$.

$X\cdot 0{,}04P=0{,}4P$
$X=10$

Ответ: 10 месяцев.
За правильные расчёты – 5 баллов.

3. Яблочная

Функция предложения яблок имеет вид $Q_s=100p-300$, где $Q_s$ – величина рыночного предложения яблок в килограммах, а $p$ – цена одного килограмма яблок в денежных единицах (д.е.). Яблоки приобретают множество потребителей, каждый из которых имеет индивидуальную функцию спроса $q_d=12-p$, где $q_d$ – величина индивидуального спроса каждого потребителя на яблоки в килограммах. Известно, что в равновесии суммарная выручка производителей яблок составила $1800$ д.е. Определите число потребителей на рынке.

Решение

Зная равновесную выручку, можно найти равновесную цену товара:

$\begin{array}{l} pQ=1800 \quad \textbf{ За формулу - 2 балла} \\ p(100p-300)-1800\end{array}$

Это квадратное уравнение имеет два корня: $-3$ и $6$. Цена может быть только положительной, следовательно, $p=6$. За число – 4 балла. Подставив эту цену в функцию предложения, находим равновесное количество товара $Q=100\cdot6-300=300$.

Величина спроса одного потребителя по такой цене составляет $q_d=12-6=6$.

Таким образом, каждый из потребителей покупает шесть единиц товара, а всего на рынке приобретается $300$ единиц товара. Следовательно, общее число потребителей на рынке составляет:

$\dfrac{300}{6}=50 \quad \textbf{ За число - 4 балла}$

4. Необычное предложение

На рынке некоторого товара в 2013 году функция спроса имела вид $Q=\dfrac{1000}{P}$, а функция предложения была задана уравнением $Q=\sqrt[2013]{p} +2013$. В 2014 году спрос на товар остался прежним, а предложение поменялось и теперь описывается функцией $Q=\sqrt[2014]{P}+2014$. На сколько процентов изменилась равновесная выручка производителей товара на этом рынке в 2014 году по сравнению с 2013 годом?
Решение

Выручка производителей равна $TR=P\cdot Q$. Если рынок находится в равновесии, то $Q=\dfrac{1000}{P}$. Следовательно, $TR=P\cdot \dfrac{1000}{P}=1000$. Таким образом, в равновесии выручка производителей всегда равна 1000 и не зависит от функции предложения (главное, чтобы равновесие достигалось).

Ответ: выручка не изменится (изменится на $0 \%$).
Максимум за задание – 10 баллов.