1. Четырехмерный коктейль
Для приготовления одной порции коктейля "Неустойчивое равновесие" -- фирменного коктейля бара "Economics" -- требуется 1 единица ингредиента A, 2 единицы ингредиента B, 3 единицы ингредиента C и 4 единицы ингредиента D (названия ингредиентов являются коммерческой тайной и не разглашаются). Однако владелец бара, знаменитый бармен и экономист Сэм Полуэльсон, обладает лишь ограниченными ресурсами для закупки дорогих ингредиентов. Так, на имеющиеся у него денежные средства он может купить либо 100 единиц ингредиента A, либо 200 единиц ингредиента B, либо 300 единиц ингредиента C, либо 400 единиц ингредиента D в день.
Какое максимальное число порций фирменного коктейля сможет приготовить Сэм за день?
- Экономическое
Найдем экономические издержки производства одной единицы коктейля, выраженные вединицах, скажем, ингредиента A.
Явно мы тратим на производство единицы коктейля одну единицу ингредиента A. Неявно тратим:- одну единицу A, от которой отказываемся, покупая две необходимые для коктейля единицы B;
- oдну единицу A, от которой отказываемся, покупая три необходимые для коктейля единицы C;
- одну единицу A, от которой отказываемся, покупая четыре необходимые для коктейля единицы D.
Таким образом, экономические издержки производства одной единицы коктейля равны $1+1+1+1=4$ единицы ингредиента A.
Поскольку всего имеется 100 единиц ингредиента A, то максимальное число порций коктейля, которое можно приготовить,
равно $100/4 = 25$ порций. - Математическое
Понятно, что бюджетное ограничение Сэма имеет вид
$pA + (p/2)B + (p/3)C + (p/4)D = 100p$,
где $p$- цена ингредиента A, а $A$, $B$, $C$, $D$- количества соответствующих ингредиентов.
Также понятно, что количество порций коктейля будет максимально, если Сэм будет тратить все деньги, и если ингредиенты будут закупаться строго в нужной пропорции.
Пусть $Q$- количество порций коктейля. Тогда пропорции соблюдаются, если $A=Q$, $B=2Q$, $C=3Q$, $D=4Q$.
Подставляя эти равенства в уравнение бюджетного ограничения, получаем:
$pQ + (p/2) \cdot 2Q + (p/3) \cdot 3Q + (p/4) \cdot 4Q = 100p \Rightarrow Q = 25.$
2. Эластичностный конфликт поколений
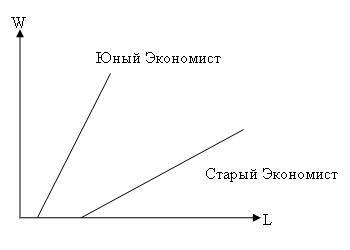
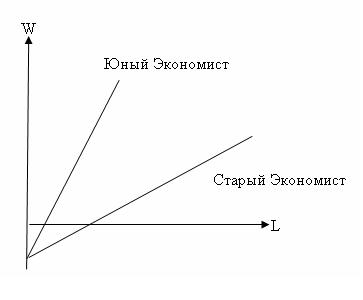
Поспорил как-то Юный Экономист со Старым Экономистом о том, чья кривая предложения труда эластичнее при одном и том же уровне заработной платы.
- Конечно, моя, - раздраженно доказывал Старый Экономист,- ты посмотри, какой у нее наклон! Да и при нулевой зарплате я готов на большее! А если мне ее еще и поднимут...
- А ты разве забыл, что эластичность и наклон - совсем не одно и то же?! Эластичнее моя кривая предложения, так как она ближе к началу координат. А там, говорят, эластичность чуть ли не единичная! - гордо отвечал Юный Экономист.
Спорили они так до вечера, пока не пришел Умный Экономист и не разрешил их спор. Попробуйте и вы сделать то же самое: выясните, чья кривая предложения труда эластичнее при каждом конкретном уровне заработной платы. Решение должно быть выполнено на основе приведенного ниже графика, на котором изображены кривые предложения труда обоих экономистов.
$L_S = c + dW \Rightarrow E_S = \frac{dW}{c + dW} = \frac{W}{c/d + W}$
Таким образом, эластичность предложения при конкретном значении заработной платы зависит только от отношения $c/d$.
$(-c/d)$ - уровень зарплаты, при котором величина предложения равна 0. В данном случае эта точка не имеет экономического смысла, однако графики до~нее достроить можно. Станет видно, что эти функции предложения труда имеют одну и ту же точку пересечения с осью $W$ и, следовательно, имеют одинаковую эластичность при каждом уровне зарплаты.
Если у кого-то по техническим причинам графики не придут в одну точку, то более эластичным должен быть назван тот график, у которого точка пересечения с осью $W$ выше.
3. Новогоднее предложение от монополиста
Спрос на продукцию монополиста линеен (снижение цены на 1 руб. неизменно вызывает рост величины спроса на 1 ед.), а средние издержки ее производства постоянны. Максимальная прибыль фирмы составила 4036081 руб. Сколько единиц продукции выпустила фирма?
Аналитическое:
Пусть $P_d = a - bQ$, $AC = c$. Тогда $TC = cQ$. По условию, $b = 1$.
$MR = a - 2Q = MC = c \Rightarrow Q^* = \frac{{a - c}}{2}$;
$\pi _{max } = \left( {a - \frac{{a - c}}{2}} \right) \cdot \frac{{a - c}}{2} - c \cdot \frac{{a - c}}{2} = \left( {\frac{{a - c}}{2}} \right)^2 = \left( {Q^*} \right)^2;\\ Q^* = \sqrt {\pi _{\max } } = 2009$.
Геометрическое:

Наклон кривой спроса равен 1. Поэтому
$\left. \begin{array}{r} OF = OE\\ OB = BE\end{array} \right\} \Rightarrow \frac{OF}{OB} = 2.$
В силу подобия $\bigtriangleup FOB$ и $\bigtriangleup FCA$,
$\frac{{FC}}{{CA}} = \frac{FO}{OB} = 2$.
Получаем:
$ \pi _{\max } = S_{\bigtriangleup FCA} = 0{,}5 \cdot CA \cdot FC = 0{,}5 \cdot CA \cdot 2CA = CA^2$.
Таким образом, в данном случае максимальная прибыль фирмы численно равна квадрату оптимального выпуска:
$Q^* = \sqrt {\pi _{\max } } = \sqrt{4036081} = 2009$.
4. Неравенство среднедушевых доходов
Некое общество состоит из двух социальных групп, внутри каждой из которых доход распределен равномерно. Известно, что среднедушевой доход в первой группе составляет 5 тыс. руб. в месяц, во второй – 25 тыс. руб. в месяц, а во всем обществе среднедушевой доход составляет 20 тыс. руб. в месяц. Определите значение коэффициента Джини для этого общества.
Обозначим количество членов более бедной социальной группы за $N_1$, более богатой - за $N_2$, а доходы групп соответственно за $I_1$ и $I_2$. Тогда:
$\frac{I_2+I_1}{N_2+N_1} = 20;\quad \frac{I_1 }{N_1 } = 5; \quad \frac{I_2 }{N_2 } = 25; \\ I_1 = 5N_1;\quad I_2 = 25N_2; \quad \frac{25N_2 + 5N_1 }{N_2 + N_1 } = 20; \\ 25N_2 + 5N_1 = 20N_2 + 20N_1; \quad N_2 = 3N_1;\\ \frac{N_1 }{N_2 + N_1} = 0{,}25; \quad \frac{I_1 }{I_2 + I_1} = \frac{5N_1}{75N_1 + 5N_1} = 0{,}0625$.
Кривая Лоренца будет иметь следующий вид:
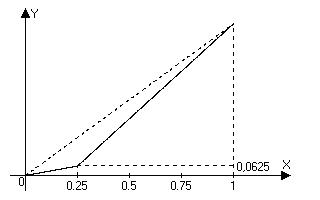
Построив ее, легко посчитать коэффициент Джини:
$G = \frac{{0{,}5 - 0{,}5\cdot0{,}25\cdot0{,}0625 - 0{,}5\cdot(1 + 0{,}0625)\cdot0{,}75}}{{0{,}5}}=0{,}1875$.