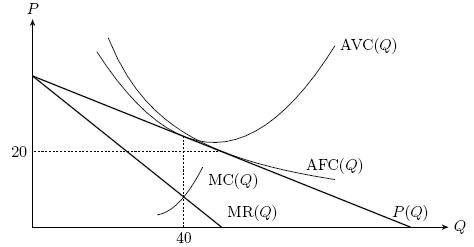
1. Простая задача на спрос и предложение

Первоначально на японском рынке mp3-плееров ежемесячно продавалось 50 тыс. плееров по цене 1000 йен. В момент X телефоны со встроенными mp3-плеерами подешевели, что спустя некоторое время привело к уменьшению объема продаж плееров на 19%. Затем, в момент Y, начал работать новый завод по производству mp3-плееров, расположенный в Китае, и рыночная цена плеера упала на 25%. Определите новые параметры равновесия на рынке mp3-плееров, если известно, что всё это время спрос и предложение на данном рынке обладали постоянной ценовой эластичностью, по модулю равной 2.

Решение

Спрос и предложение - функции постоянной эластичности, равной по модулю 2, значит, $Q_d = a/P^2$; $Q_s = bP^2$.

Пусть величины с индексом "0" - параметры первоначального равновесия, "1" - параметры равновесия после первого изменения, "2" - параметры равновесия после второго изменения.

Основная "фишка" здесь в том, что в условии напрямую не сказано, сдвиги каких кривых произошли, в то время как от этого в итоге зависит численный ответ. Для того чтобы понять, какие кривые сдвигались, нужно правильно проинтерпретировать текстовое условие; это является существенным элементом решения.

Первое изменение заключалось в падении цены товара-заменителя: кривая спроса сместилась влево-вниз, мы двигались вдоль кривой предложения. Поэтому

$ 0{,}81 = \frac{{Q_1 }} {{Q{}_0}} = \frac{{bP_1^2 }} {{bP_0^2 }} = \left( {\frac{{P_1 }} {{P_0 }}} \right)^2 \Rightarrow \frac{{P_1 }} {{P_0 }} = 0{,}9. $

Второе изменение - это появление новых дешевых производственных мощностей: кривая предложения сдвинулась вправо-вниз, мы двигались вдоль кривой спроса. Поэтому

$$ \frac{{Q_2 }} {{Q_1 }} = \frac{{a/P_2^2 }} {{a/P_1^2 }} = \left( {\frac{{P_2 }} {{P_1 }}} \right)^{ - 2} = \left( {\frac{3} {4}} \right)^{ - 2} = \frac{{16}} {9}.$$

В итоге имеем:
$$\frac{P_2 }{P_0} = \frac{P_2}{P_1} \cdot \frac{P_1}{P_0} = 0{,}75 \cdot 0{,}9 = 0{,}675 \Rightarrow P_2 = 675;\\ \frac{Q_2}{Q_0} = \frac{Q_2}{Q_1} \cdot \frac{Q_1}{Q_0} = \frac{16}{9} \cdot \frac{81}{100} = 1{,}44 \Rightarrow Q_2 = 72.$$

2. Задача про пиратов

Пират Джим производит джин и продает его днем в своем баре по цене 28 гульденов за пинту. Функция издержек Джима на производство джина задается уравнением $\operatorname{TC}(Q)=Q^2$, где $Q$ — произведенное количество джина в пинтах. А ночью Джим вместе со своим приятелем пиратом Роном выходит «на дело» в море, где и потребляет часть произведенного им чистого джина. Джим старается оставить на ночь как можно больше джина, поскольку за прибылью он не гонится, а гульдены ему нужны только для оплаты факторов производства.

В отличие от Джима пират Рон не любит чистый джин и готовит себе коктейль «Веселый Роджер» (на полпинты джина треть пинты рома), тратя на ингредиенты для его приготовления 220 гульденов, заработанные ночным разбоем. Джин пират Рон покупает в лавке Джима, а ром — в соседней лавке по 18 гульденов за пинту.

Сколько рома и сколько джина потребляют на двоих за ночь пират Рон и пират Джим?

Решение

Пусть $q_s$ — количество джина, которое Джим производит для себя, а $q_m$ — для продажи на рынок. Тогда $Q = q_s + q_m$, $\operatorname{TC} = (q_s + q_m )^2$. Поскольку выручку он получает только от тех единиц продукции, которые проданы на рынок, $\operatorname{TR} = 28q_m$. Так как всю прибыль он тратит на производство для себя, выполняется: $28q_m - (q_s + q_m )^2 = 0$. При этом условии Джим максимизирует $q_s$:

\begin{gather} 28q_m = (q_s + q_m )^2 \\ q_s + q_m = \sqrt {28q_m } \\ q_s = \sqrt {28q_m } - q_m \\ q'_s = \frac{{\sqrt {28} }}{{2\sqrt {q_m } }} - 1 = 0\end{gather}

Отсюда $q_m = 7$, $q_s = \sqrt {28\cdot7} - 7 = 7$ — Джим выпивает за вечер 7 пинт джина.

Одна порция коктейля, включающая полпинты джина и треть пинты рома, стоит Рону $\frac{1}{2}\cdot 28 + \frac{1}{3}\cdot 18=20$ гульденов. Значит, на свои 220 гульденов он сможет купить ингредиентов и приготовить 11 порций коктейля, то есть выпить $\frac{11}{3}$ пинт рома и $\frac{11}{2}$ пинт джина.

3. Графическая-2009

Данные об экономической ситуации, с которой столкнулась некая фирма, представлены графически (даны графики выручки, предельных издержек и средней прибыли):

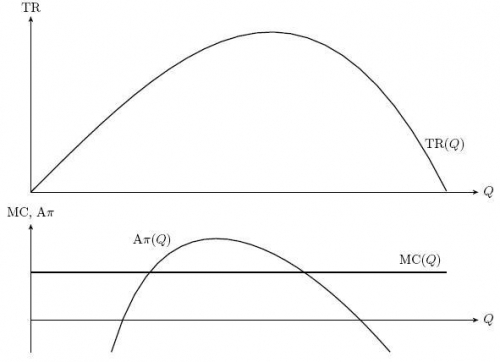
Масштаб по оси $Q$ на обоих графиках одинаковый. Определите графически оптимальный для данной фирмы объем производства и подробно опишите процесс решения.

Решение

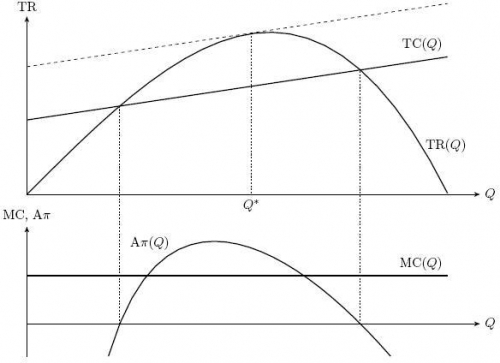
В точках, где средняя прибыль равна 0, общая прибыль также равна 0.
В этих точках $TR = TC$, чем и можно воспользоваться, восстанавливая график $TC$, являющийся в данном случае прямой, так как $MC$ постоянны (как известно, по двум точкам прямую всегда можно восстановить).
Затем находим с помощью касательной точку, в которой наклоны $TR$ и $TC$ равны, то есть $MR=MC$, и получаем $Q*$. Как видим, при этом объеме выпуска расстояние по вертикали между графиками $TR$ и $TC$ (то есть прибыль фирмы) как раз наибольшее.

4. Копыта, рога и украденная прибыль

Воробьян Кисин, владелец контрольного пакета акций ЗАО «Копыта и рога», являющегося монополистом на рынке весьма специфической продукции, ежеквартально проверяет, как идут дела в его фирме. Из последнего отчета, составленного для Кисина главным менеджером фирмы Е. Бондером главный акционер узнал, что общие издержки производства продукции за последний квартал составили 134 тыс. рублей, а прибыль несколько снизилась по сравнению с предыдущим кварталом и составила 66 тыс. руб.

Кисин, получивший отличное экономическое образование и помнивший квартальную функцию издержек фирмы $(TC=Q^2+3Q+4)$, наоборот, ждал роста прибыли и потому стал сомневаться в правильности предоставленного ему отчета. И действительно, после обстоятельной проверки выяснилось, что Бондер правильно отчитался об издержках фирмы в точке оптимума, но несколько занизил уровень прибыли (которая в действительности повысилась). Как выяснилось позднее, скрытая часть прибыли была потрачена Бондером на билет первого класса в один из крупных южноамериканских городов.

Какова минимально возможная цена этого билета?

Решение

По сути, нам нужно оценить минимальный размер прибыли, которую в оптимуме могла получить компания.

Найдем сначала оптимальный выпуск фирмы:
$TC(Q_m)=Q_m^2+3Q_m+4=134\Rightarrow Q_m=10$.

Ключевая идея: данная фирма является монополистом, поэтому в оптимуме $P\geq MC$.
$MC(Q)=2Q+3$.
$P\geq MC(10)=23\Rightarrow \pi =10P-TC(10)=10P-134\geq 23\cdot10-134=96.$

Таким образом, в оптимуме фирма никак не могла получить прибыль, меньшую, чем 96 тыс. руб. Значит, минимально возможная цена билета составляет $96-66=30$ тыс. рублей.

1. В поезде «Москва-Симферополь»

В поезде «Москва — Симферополь» функция спроса пассажиров на украинские гривны описывается уравнением $Q_g^d(P_g)=6000/P_g-500$, где $Q_g^d$ - количество гривен, $P_g$ - цена гривны (в российских рублях). Лица, обычно садящиеся в Харькове и предлагающие гривны к обмену, предъявляют тем самым спрос на рубли. Соответствующая функция спроса имеет вид $Q_r^d(P_r)=1500/P_r-4000$, где $Q_r^d$ - количество рублей, $P_r$ - цена рубля (в гривнах).

Определите параметры равновесия на данном рынке:

Какое количество гривен купят пассажиры?
Какое количество рублей они продадут?
Каков будет обратный курс рубля по отношению к гривне?

Решение

По функции спроса на рубли восстановим функцию предложения гривен $Q_g^s(P_g)$. Нам нужно узнать, какое количество гривен готовы продать украинцы, если цена гривны в рублях составляет $P_g$.

Если цена гривны в рублях составляет $P_g$, то цена рубля в гривнах равна $1/P_g$. По этой цене украинцы будут готовы купить $Q_r^d(1/P_g)=\frac{1500}{1/P_g}-4000=1500P_g-4000$ рублей.

Но раз цена гривны в рублях составляет $P_g$, то купить $1500P_g-4000$ рублей – это то же самое, что продать $\frac{1500P_g-4000}{P_g}$ гривен. Поэтому искомая функция предложения гривен имеет вид $Q_g^s(P_g)=1500-4000/P_g$. Как и полагается, она имеет положительный наклон.

Теперь легко найти рыночное равновесие: спрос на гривны должен быть равен их предложению. $6000/P_g-500=1500-4000/P_g$, откуда $P_g=5$ рублей за гривну. Поскольку обратный курс рубля должен показывать количество рублей за одну гривну, то найденная величина как раз им и является. При $P_g=5$
$Q_g=700$, $Q_r=5\cdot700=3500$.

2. Крококосбургер и время на готовку

Робинзон собирает кокосы и ловит крокодилов, однако, к сожалению, по отдельности кокосы и крокодилы полезности ему не приносят. Поэтому из них он готовит особое блюдо — крококосбургер. Для приготовления одного крококосбургера нужен один крокодил и три кокоса. Кроме того, на готовку Робинзону приходится тратить некоторое время, в которое уже нельзя ловить крокодилов или собирать кокосы. Занимаясь только ловлей крокодилов, Робинзон может поймать 76 крокодилов в месяц, занимаясь только сбором кокосов, он может собрать 114 кокосов в месяц, а если бы кто-нибудь поставлял ему ингредиенты и он мог заниматься только готовкой, то он бы приготовил за месяц 95 крококосбургеров. Альтернативные издержки занятия любым видом деятельности постоянны.
Какое максимальное количество Крококосбургеров в месяц может фактически приготовить и съесть Робинзон?

Решение

Пусть мы хотим приготовить $X$ бургеров. Тогда мы должны собрать $X$ крокодилов и $3X$ кокосов.
Ловя $X$ крокодилов, мы отказываемся от приготовления $95X/76 = 1,25X$ бургеров.
Собирая $3X$ кокосов, мы отказываемся от приготовления $3X*95/114 = 2,5X$ бургеров.
Итого у нас остается времени, чтобы приготовить $95-1,25X- 2,5X=95-3,75X$ бургеров.

Очевидно, что в оптимуме у нас нет излишков времени, то есть у нас остается времени на приготовление ровно того количества бургеров, на которое мы собрали ресурсов, поэтому
$95-3,75X=X$, откуда $X = 20$.

3. Два касания

Фирма "В два касания" является монополистическим конкурентом на рынке волейбольных мячей. В последнее время владельцу фирмы Н. Е.Удачнику можно только посочувствовать: его бизнес переживает не лучшие времена (Кризис!). Спрос на продукцию фирмы линеен, однако в последнее время он стал настолько низким, что фирме неважно, уходить с рынка или производить 40 единиц продукции, - и это при наиболее продуманном, рациональном поведении! Средние переменные издержки при данном объеме выпуска аж втрое больше предельных, а единственным для фирмы шансом покрыть выручкой постоянные издержки было бы установление цены, равной 20.
Представьте, что вы являетесь сотрудником государственной службы, оказывающей поддержку малому бизнесу.

Проанализируйте ситуацию, в которой оказалась фирма "В два касания", графически, изобразив на одном рисунке примерные графики спроса, $MR,$ $MC,$ $AVC,$ $AFC$.
Определите уравнение кривой спроса на продукцию фирмы.
Определите величину аккордной субсидии, необходимой для выведения фирмы Н. Е. Удачника на уровень безубыточности.

Решение

В оптимуме фирме неважно, производить 40 единиц продукции или уходить с рынка, значит,

\begin{gather}MR(40) = MC(40) \\ \pi (40) = \pi (0) = - FC\\ \Downarrow\\ P(40) = AVC(40)\end{gather}

Более того, раз фирма не может получить прибыль большую, чем $(-FC)$, то в других точках $Pкасаться графика спроса в точке, где $Q=40$.

Из условия следует, что существует лишь единственная цена (а значит, и единственный объем выпуска), при которых выручка равна постоянным издержкам. Как легко понять из графиков выручки и постояннных издержек, такая ситуация возможна, только если при этом объеме выпуска выручка максимальна. Значит, в остальных точках выручка меньше, чем постоянные издержки, а средняя выручка (цена) - меньше, чем средние постоянные издержки. Отсюда следует, что график спроса должен касаться графика $AFC$ в точке, где $P=20$ и $MR=0$.

Пусть обратная функция спроса задается уравнением $P=a-bQ$. Тогда

$$3 = \frac{{AVC(40)}}{{MC(40)}} = \frac{{P(40)}}{{MR(40)}} = \frac{{a - b \cdot 40}}{{a - 2b \cdot 40}} \Rightarrow a = 100b.$$

Как мы выяснили, максимальную выручку фирма может получить при $P=20$. Для нашей функции спроса цена, максимизирующая выручку, равна $a/2$, и значит, $a = 40$. Функция спроса, таким образом, имеет вид $P = 40 - 0{,}4Q$.

Понятно, что величина аккордной субсидии, выводящей фирму на уровень безубыточности, должна быть в точности равна текущим убыткам фирмы (ведь после получения аккордной субсидии фирма не изменит выпуск). Значит, $S = - \pi (40) = FC = TR_{\max} = 20 \cdot 100/2 = 1000.$

Графически ситуация сводится к следующему:

Вот такие "Два касания"!

4. Кривая Лаффера, два зайца и тысячи рыб

Заботясь о сохранении редких видов рыб, государство собирается ввести на рынке черной икры потоварный налог. С помощью этой меры оно надеется не только ограничить потребление икры, но и получить средства для финансирования дорогостоящей экологической программы. Таким образом, убивая двух зайцев, можно будет спасти тысячи рыб!
Экономисты правительства оценили для данного рынка кривую Лаффера при введении потоварного налога:$$T=\frac{200900t}{(1+t)^2},$$ где $t$ – ставка налога (в. тыс. руб.), $T$ – общая сумма налоговых поступлений (также в тыс. руб.). На сколько процентов государству удастся максимально сократить объем потребления икры, если с помощью налога нужно собрать не менее 48216 тыс. руб. (именно столько стоит программа)?

Решение

Найдем, какие ставки налога обеспечат как минимум нужную сумму:
$T=\frac{200900t}{(1+t)^2}\geq 48216\Rightarrow \frac{2}{3}\leq t\leq\frac{3}{2}$.
Государство стремится минимизировать объем продаж черной икры $\Rightarrow$ оно установит максимальную налоговую ставку из всех подходящих: $t=1,5$.

Для того чтобы найти изменение рыночного объема, вспомним, что сумма налоговых поступлений при введении потоварного налога равна $t\cdot Q(t)$, где $Q(t)$ - равновесный объем, который установится на рынке при введении налога по ставке $t$.
$T=\frac{200900t}{(1+t)^2}=t\cdot Q(t)\Rightarrow Q(t)=\frac{200900}{(1+t)^2}$.

До налогообложения рыночный объем равнялся $Q(0)=200900$.
После введения налога $Q=Q(1,5)=\frac{200900\cdot 4}{25}$.
Отношение объемов равно $\frac{4}{25}$,т.е. объем продаж икры удастся сократить на $84\%$.

1-й тур: Задачи

1. Простая задача на спрос и предложение

2. Задача про пиратов

3. Графическая-2009

4. Копыта, рога и украденная прибыль

3-й тур: Задачи

1. В поезде «Москва-Симферополь»

2. Крококосбургер и время на готовку

3. Два касания

4. Кривая Лаффера, два зайца и тысячи рыб

Тест

1. Возможности фермера (вопрос из теста)